4540

Free-water volume fraction increases nonlinearly across the lifespan in healthy human brain white matter areas
Tomasz Pieciak1, Guillem París1, Dani Beck2,3, Ivan I. Maximov3,4, Antonio Tristán-Vega1, Rodrigo de Luis-García1, Lars T. Westlye2,3,5, and Santiago Aja-Fernández1
1Laboratorio de Procesado de Imagen (LPI), Universidad de Valladolid, Valladolid, Spain, 2Department of Psychology, University of Oslo, Oslo, Norway, 3NORMENT, Division of Mental Health and Addiction, Oslo University Hospital & Institute of Clinical Medicine, University of Oslo, Oslo, Norway, 4Western Norway University of Applied Sciences, Bergen, Norway, 5KG Jebsen Centre for Neurodevelopmental Disorders, University of Oslo, Oslo, Norway

Synopsis

The free-water (FW) volume fraction $$$f$$$ is a sensitive diffusion MRI biomarker correlated with microstructural alterations in the human brain. This paper studies the variations in the FW volume fraction $$$f$$$ in healthy human brain white matter (WM) across the lifespan from a set of 248 female and 140 male subjects. Our study reveals positive nonlinear correlations of the volume fraction $$$f$$$ with age over the WM regions and suggests a heteroscedastic nature and age-dependent intra-region-of-interest variability of $$$f$$$ across the lifespan.

Introduction

The fluctuations in microstructural properties of the brain are a consequence of physical and inherent biological processes, including cognition1,2,3, ageing13 and development of neurodegenerative diseases6,7. To model the free-water (FW) component, a bi-tensor signal representation has been proposed9, i.e. the tissue compartment that displays a slow diffusion by a second-order tensor and a free-water isotropic component with a fixed diffusivity at $$$D_0 = 3.0 \times 10^{-3} \ \mathrm{mm}^2/\mathrm{s}$$$. Several studies have shown that the FW respond to pathological processes that modify the interstitial extracellular space4,25,26. Besides, the FW estimate decreases the number of false-positive streamlines in Diffusion Tensor Imaging (DTI) based tractography10 and improves the reproducibility of DTI-based biomarkers11. In this paper, we investigate the changes in the FW volume fraction $$$f$$$ with age. Our study is not limited to modelling the slow diffusion component via the DT as it employs a more general diffusion representation using a continuous mixture of axis-symmetric second-order tensors.

Materials and methods

Data: In total, 388 healthy patients (248F/140M), aged (mean$$$\pm$$$std.dev: $$$61.09\pm12.11$$$/$$$64.7\pm14.79$$$), were scanned using a 3T General Electric MR750 scanner (GE, Waukesha, WI) equipped with a 32 channel head coil. Diffusion MR data were acquired with an EPI sequence with TE/TR 83.1/8150 ms, flip angle 90$$$^\circ$$$, voxel resolution $$$2\times 2 \times 2 \ \mathrm{mm}^3$$$. The data include two-shells at $$$b=1000\ \mathrm{s}/\mathrm{mm}^2$$$ (60 diffusion gradient directions) and $$$b=2000\ \mathrm{s}/\mathrm{mm}^2$$$ (30 directions), and 7 non-diffusion-diffusion MR acquisitions in a reversed phase-encoding direction13.

Data preprocessing: Diffusion MR data were preprocessed using the following pipeline27: noise removal using the MP-PCA approach15, Gibbs ringing artefacts correction16, susceptibility-induced, head movement and eddy current distortions correction with FSL17. Eventually, the dataset underwent a rigorous quality assurance test in terms of noise, motion and other artefacts19, followed by manual outliers and verification.

Free-water estimation: We estimated the FW volume fraction $$$f$$$ from two-shells using the FW spherical mean (FW-SM) approach20 that assumes the diffusion is modelled using a continuous mixture of axis-symmetric second-order tensors in the space of orientations:$$\frac{S(\mathbf{g},b)}{S_0}=(1-f)\iint_{\Omega}\Phi(\mathbf{v})\exp\left(-b(\lambda_{||}-\lambda_\perp)(\mathbf{v}^T\mathbf{g})^2-b\lambda_\perp\right)d\mathbf{v}+f\exp(-bD_0), $$with $$$\lambda_{||}/\lambda_{\perp}$$$ being the longitudinal/perpendicular diffusivity that satisfy $$$0\leq\lambda_\perp\leq\lambda_{||}\leq D_0$$$, and $$$\Phi(\mathbf{v})\geq0$$$ is the fODF, and $$$\Omega = \left\{\mathbf{v}\in\mathbb{R}^3\colon||\mathbf{v}||=1\right \}$$$. To calculate the orientationally-averaged diffusion MR signal that is required by the FW-SM approach, we decompose the signal using a spherical harmonics (SHs) basis at order of $$$L=6$$$ via an inverse linear problem with a Laplace-Beltrami regularization of $$$\lambda=0.001$$$21,22. The FW diffusivity has been fixed to $$$D_0=3.0\times 10^{-3}\ \mathrm{mm}^2/\mathrm{s}$$$.

WM atlas: We estimated the fractional anisotropy (FA) for each subject with the standard DTI signal representation14 and registered the FAs to the template in the standard space via a non-linear registration18. The region-of-interests (ROIs) over the WM in subject native spaces were retrieved from the JHU DTI-based atlas23 followed by a morphological binary erosion with a structural element of size $$$2\times 2\times 2$$$ used to remove possible misregistration outliers. Finally, the volume fractions $$$f$$$ over each ROI were aggregated to one representative value using a median operator.

Statistical analysis: To model the changes of FW volume fraction $$$f$$$ across the lifespan, we use the nonlinear quantile regression (QR) technique24 that estimates the conditional median of the fraction $$$f$$$ given the explanatory variable $$$Age$$$
$$Q(\tau|Age)=\beta_0+\beta_1 Age+\beta_2 Age^2+\beta_3 Age^3\;\;\mathrm{with}\;\;\beta_k\in\mathbb{R}.$$
Applying the QR allows for modelling the heteroscedastic nature of the volume fraction $$$f$$$ without assumptions on the distributional properties of the data. We estimate three quantiles, including $$$\tau=0.05$$$ (5th percentile), $$$\tau=0.5$$$ (median), and $$$\tau=0.95$$$ (95th percentile).

Results

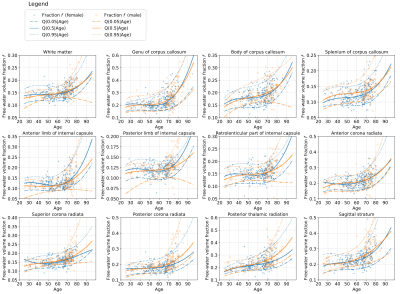
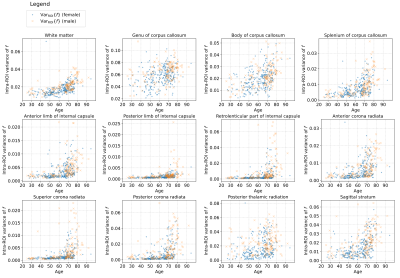
  • Fig.1 and Fig.2 present the scatter graphs of a free-water volume fraction $$$f$$$ and its intra-ROI variability across the lifespan retrieved separately for female and male subjects. We observe a positive tendency of changes in the parameter $$$f$$$ and its intra-ROI variability across the lifespan over each ROI and, in general, over the WM area.
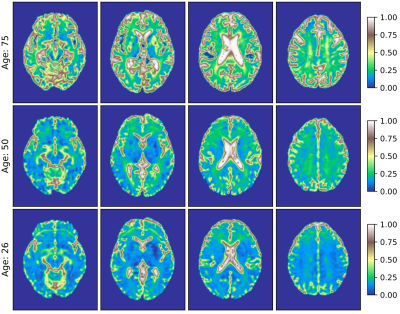
  • Fig.3 visually inspects the FW volume fraction $$$f$$$ in transverse planes for three selected male subjects at the age of 75, 50 and 26, all combined together in the standard space. We recognise the positive changes in $$$f$$$ with age.

Discussion and conclusions

In this paper, we studied the sensitivity of the FW volume fraction $$$f$$$ in healthy male and female brain white matter throughout the lifetime. Our study has led to the following conclusions:
  1. The volume fraction $$$f$$$ shows a positive correlation with age that is consistent with the previous report5, and additionally, it exhibits a nonlinear gain after the age of 60. Although the FW-SM approach revealed smaller values of $$$f$$$ in comparison to10, recent study20 has shown that the bi-tensor approach tends to overestimate the FW volume fraction due to the single fibre assumption in a voxel.
  2. The volume fraction $$$f$$$ uncovered a heteroscedastic nature in a function of age, i.e. the variance of $$$f$$$ increases with age. To correctly model this phenomenon, we employed the nonlinear QR statistical technique24 that handles a heteroscedastic behaviour of the data. In comparison to a standard (non)linear regression, we were able to model the conditional median of $$$f$$$ with no assumptions on the statistical distribution of the parameter.
  3. The intra-ROI variability of the volume fraction $$$f$$$ has shown a positive correlation with age. These results might suggest a variable sensitivity of the brain intra-ROI tissue to ageing.

Acknowledgements

The authors acknowledge Ministerio de Ciencia e Innovación of Spain with research grant RTI2018-094569-B-I00. Tomasz Pieciak acknowledges the Polish National Agency for Academic Exchange for the grant PN/BEK/2019/1/00421 under the Bekker programme and the Ministry of Science and Higher Education (Poland) under the scholarship for outstanding young scientists (692/STYP/13/2018).

References

  1. Maillard, P., Fletcher, E., Singh, B., Martinez, O., Johnson, D. K., Olichney, J. M., et al. (2019). Cerebral white matter free water: A sensitive biomarker of cognition and function. Neurology, 92(19), e2221-e2231.
  2. Edde, M., Theaud, G., Rheault, F., Dilharreguy, B., Helmer, C., Dartigues, et al. (2020). Diffusion MRI free water is a sensitive marker of age-related changes in the cingulum. bioRxiv, 867606.
  3. Gullett, J. M., O’Shea, A., Lamb, D. G., Porges, E. C., O’Shea, D. M., Pasternak, et al. (2020). The association of white matter free water with cognition in older adults. NeuroImage, 219, 117040.
  4. Raghavan, S., Reid, R. I., Przybelski, S. A., Lesnick, T. G., Graff-Radford, J., Schwarz, C. G., et al. (2021). Diffusion models reveal white matter microstructural changes with ageing, pathology and cognition. Brain communications, 3(2), fcab106.
  5. Chad, J. A., Pasternak, O., Salat, D. H., & Chen, J. J. (2018). Re-examining age-related differences in white matter microstructure with free-water corrected diffusion tensor imaging. Neurobiology of aging, 71, 161-170.
  6. Kubicki, M., McCarley, R., Westin, C. F., Park, H. J., Maier, S., Kikinis, R., et al. (2007). A review of diffusion tensor imaging studies in schizophrenia. Journal of psychiatric research, 41(1-2), 15-30.
  7. Bergamino, M., Walsh, R. R., & Stokes, A. M. (2021). Free-water diffusion tensor imaging improves the accuracy and sensitivity of white matter analysis in Alzheimer’s disease. Scientific reports, 11(1), 1-12.
  8. Westlye, L. T., Walhovd, K. B., Dale, A. M., Bjørnerud, A., Due-Tønnessen, P., Engvig, A., et al. (2010). Life-span changes of the human brain white matter: diffusion tensor imaging (DTI) and volumetry. Cerebral cortex, 20(9), 2055-2068.
  9. Pierpaoli, C., & Jones, D. K. (2004). Removing CSF contamination in brain DT-MRIs by using a two-compartment tensor model. In International Society for Magnetic Resonance in Medicine Meeting (p. 1215).
  10. Pasternak, O., Sochen, N., Gur, Y., Intrator, N., & Assaf, Y. (2009). Free water elimination and mapping from diffusion MRI. Magnetic Resonance in Medicine, 62(3), 717-730.
  11. Albi, A., Pasternak, O., Minati, L., Marizzoni, M., Bartrés‐Faz, D., Bargallo, N., et al. (2017). Free water elimination improves test–retest reproducibility of diffusion tensor imaging indices in the brain: A longitudinal multisite study of healthy elderly subjects (Vol. 38, No. 1, pp. 12-26).
  12. Basser, P. J., Mattiello, J., & LeBihan, D. (1994). MR diffusion tensor spectroscopy and imaging. Biophysical journal, 66(1), 259-267.
  13. Beck, D., de Lange, A. M. G., Maximov, I. I., Richard, G., Andreassen, O. A., Nordvik, J. E., & Westlye, L. T. (2021). White matter microstructure across the adult lifespan: A mixed longitudinal and cross-sectional study using advanced diffusion models and brain-age prediction. NeuroImage, 224, 117441.
  14. Basser, P. J., Mattiello, J., & LeBihan, D. (1994). MR diffusion tensor spectroscopy and imaging. Biophysical journal, 66(1), 259-267.
  15. Veraart, J., Novikov, D. S., Christiaens, D., Ades-Aron, B., Sijbers, J., & Fieremans, E. (2016). Denoising of diffusion MRI using random matrix theory. Neuroimage, 142, 394-406.
  16. Kellner, E., Dhital, B., Kiselev, V. G., & Reisert, M. (2016). Gibbs‐ringing artifact removal based on local subvoxel‐shifts. Magnetic resonance in medicine, 76(5), 1574-1581.
  17. Smith, S. M., Jenkinson, M., Woolrich, M. W., Beckmann, C. F., Behrens, T. E., Johansen-Berg, H., et al (2004). Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage, 23, S208-S219.
  18. Jenkinson, M., Bannister, P., Brady, M., & Smith, S. (2002). Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage, 17(2), 825-841.
  19. Roalf, D. R., Quarmley, M., Elliott, M. A., Satterthwaite, T. D., Vandekar, S. N., Ruparel, et al. (2016). The impact of quality assurance assessment on diffusion tensor imaging outcomes in a large-scale population-based cohort. Neuroimage, 125, 903-919.
  20. Tristán‐Vega, A., París, G., de Luis‐García, R., & Aja‐Fernández, S. (2021). Accurate free‐water estimation in white matter from fast diffusion MRI acquisitions using the spherical means technique. Magnetic Resonance in Medicine.
  21. Descoteaux, M., Angelino, E., Fitzgibbons, S., & Deriche, R. (2007). Regularized, fast, and robust analytical Q‐ball imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 58(3), 497-510.
  22. Afzali, M., Knutsson, H., Özarslan, E., & Jones, D. K. (2021). Computing the orientational-average of diffusion-weighted MRI signals: A comparison of different techniques. Scientific Reports, 11(1), 1-16.
  23. Mori, S., Wakana, S., Van Zijl, P. C., & Nagae-Poetscher, L. M. (2005). MRI atlas of human white matter. Elsevier.Koenker, R., & Hallock, K. F. (2001). Quantile regression. Journal of economic perspectives, 15(4), 143-156.
  24. Koenker, R., & Hallock, K. F. (2001). Quantile regression. Journal of economic perspectives, 15(4), 143-156.
  25. Metz, M. C., Molina-Romero, M., Lipkova, J., Gempt, J., Liesche-Starnecker, F., Eichinger, P., et al. (2020). Predicting glioblastoma recurrence from preoperative MR scans using fractional-anisotropy maps with free-water suppression. Cancers, 12(3), 728.
  26. Dumont, M., Roy, M., Jodoin, P. M., Morency, F. C., Houde, J. C., Xie, Z., et al. (2019). Free water in white matter differentiates MCI and AD from control subjects. Frontiers in aging neuroscience, 11, 270.
  27. Maximov, I. I., Alnæs, D., & Westlye, L. T. (2019). Towards an optimised processing pipeline for diffusion magnetic resonance imaging data: Effects of artefact corrections on diffusion metrics and their age associations in UK Biobank. Human Brain Mapping, 40(14), 4146-4162.

Figures

Fig. 1 Estimated free-water volume fractions $$$f$$$ and their trajectories across the lifespan including the WM area and selected ROIs from the JHU DTI-based atlas. The solid lines show the quantiles $$$Q(0.5|Age)$$$ (50th percentiles), the lower dotted-dashed lines indicate quantiles $$$Q(0.05|Age)$$$ (5th percentiles), and the upper dotted lines present the quantiles $$$Q(0.95|Age)$$$ (95th percentiles), all calculated separately for female and male subjects.

Fig. 2 The intra-ROI variance, $$$\mathrm{Var}_\mathrm{ROI}\{f\}$$$,of the free-water volume fraction $$$f$$$ parameter as a function of $$$Age$$$. The asterisks represent the sample variance of the parameter $$$f$$$ in each ROI, all calculated separately for female and male subjects.

Fig. 3 Visual inspection of a FW volume fraction $$$f$$$ in transverse planes for three male subjects at the age of 75 (top), 50 (middle) and 26 (bottom), all displayed in the standard space.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
4540
DOI: https://doi.org/10.58530/2022/4540