Synopsis

A novel k-space learning based framework is introduced to compensate for bulk motion artifacts in UTE/ZTE radial acquisition schemes. The motion during the scan is modeled as rigid, and is parametrized by time varying translation and rotation parameters. The time varying parameters are used to define a forward model, which transforms the undistorted image to distorted k-t space data. The error between the measured and computed k-t space data is used to optimize the image and the deformation parameters using ADAM optimization. A multi-scale approach is used to minimize the computational complexity.

Summary

The superior acoustic properties and high signal to noise ratio of short echo time (UTE/ZTE) 3D radial MRI methods make them attractive in applications, including pediatric brain imaging. Similar to other sequences, this approach is vulnerable to bulk motion in the pediatric setting. The main focus of this abstract is to introduce a novel motion compensation algorithm. The motion during the acquisition is modeled as rigid, parameterized by time varying rotation and translation parameters. The joint estimation of the deformation parameters and image are formulated as an optimization scheme, which is solved using deep-learning libraries.

Introduction

The quieter nature of ultra-short/zero echo-time 3D radial sequences make them attractive in the pediatric setting. Pediatric MRI scanning has unique difficulties, especially in the difficulty of preventing, detecting or correcting scan failures and artifacts due to motion. Scanning failure rates as high as 50% and 35% for children between 2–5 and 6–7 years, respectively, have been reported. Several motion compensation strategies had been introduced for brain imaging applications [1-3], which uses motion tracking mechanisms, estimation of motion using k-space navigators, and prospective motion correction. Most of these approaches requires specialized pulse sequences or hardware. Recently several authors have proposed to perform low-resolution reconstructions of sub-groups of 3-D radial acquisitions, followed by image registration to estimate the motion parameters, and motion parameter aware recovery [4].

The main focus of this work is to introduce a learning-based motion compensation approach, which does not require additional hardware or sequence modifications for navigators. The proposed framework capitalizes on the auto-differentiation ability of modern deep learning libraries and basic Fourier transform properties.

Methods

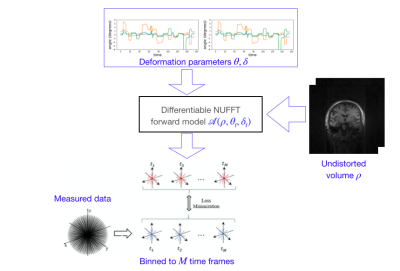
Head motion during the scan is modeled as rigid-body motion. The time-varying rotation $$$\theta_t$$$ and translation $$$\delta_t$$$ parameters are assumed to change in a piecewise smooth fashion during the acquisition. We note that rotation induced motion changes can be modeled as the non-uniform Fourier transform of an undistorted image volume with a rotated k-space trajectory $$$F_{\mathbf k} \left( \rho\left(\mathbf R_{\boldsymbol\theta}\mathbf x\right)\right) = F_{R_{\boldsymbol\theta}\mathbf k} \left(\mathbf \rho(\mathbf x)\right),$$$ where $$$F_{\mathbf k}$$$ denotes a non-uniform Fourier transform of $$$\rho$$$ evaluated at $$$\mathbf k.$$$ Similarly, translation motion can be modeled as a phase modulation in the Fourier domain. $$$F_{\mathbf k}\left(\rho(\mathbf x-\boldsymbol \delta)\right) = F_{\mathbf k}\left(\rho(\mathbf x)\right)\cdot \exp(-j\mathbf k^T\boldsymbol \delta)$$$. The impact of time varying rigid body motion can thus be modeled by a non-uniform Fourier transform (NUFFT) forward model, parameterized by the time-varying motion parameters $$$\boldsymbol \theta_t$$$ and $$$\boldsymbol \theta_t$$$, applied on a undistorted image:
$$\mathbf b_t = \underbrace{\exp(-j\mathbf k^T\boldsymbol \delta_t)~ \int \rho(\mathbf x) \exp\left(-j (\mathbf R_{\boldsymbol \theta_t} \mathbf k)^T \mathbf x \right) d\mathbf x}_{\mathcal A\left(\rho, _{\boldsymbol\theta_t,\boldsymbol \delta_t}\right)}.$$ We implement $$$\mathcal A\left(\rho, \boldsymbol\theta_t,\boldsymbol \delta_t\right)$$$ operator as a differentiable module in Pytorch.

This definition allows is to optimize for the unknowns $$$\rho, \boldsymbol \theta_t$$$, and $$$\boldsymbol \delta_t$$$ by minimizing the loss: $$\left\{\rho^*,\boldsymbol \theta_t^*, \boldsymbol \delta_t^*\right\} = \arg \min_{\rho,\boldsymbol \theta_t, \boldsymbol \delta_t} \|\mathcal A(\rho,\boldsymbol \theta_t, \boldsymbol \delta_t) - \mathbf b_t\|^2 + \lambda \left(\|\nabla_t \theta_t\|^2 +\|\nabla_t \delta_t\|^2 \right).$$ The first term is the data consistency, while the second one encourages the temporal smoothness of deformation parameters. The approach is outlined in Fig. 1. For computational efficiency, we use a multiscale refinement of $$$\rho$$$ and use alternating minimization, where we alternate between the estimation of $$$\rho$$$ and the deformation parameters: $$$\boldsymbol\theta_t, \boldsymbol\delta_t$$$.

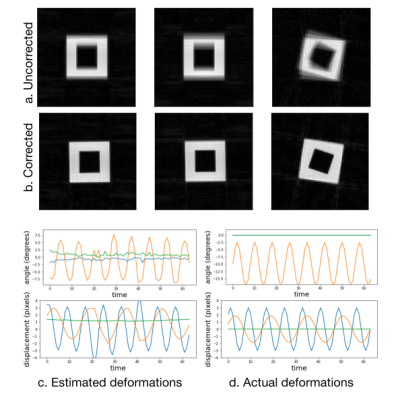
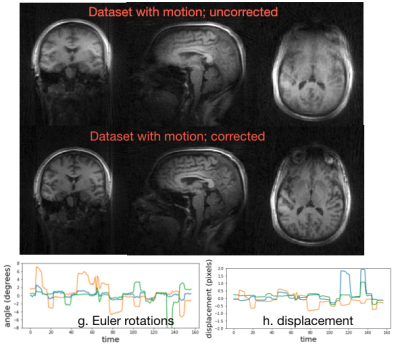
The approach was verified using a numerical simulation, where we consider a hollow cube that is translated and rotated using a 48-channel simulated array. The radial data is binned to 64 time frames and reconstructed. The utility of this approach was also studied on a 3D UTE acquisition on a normal human subject acquired on a 7T scanner with TR=3.6ms, matrix size = 192^3 and FOV = 220^3 with a 32 channel coil and an acquisition time of 5 minutes. Two acquisitions were made; the subject was instructed to stay still in the first one, while was asked to move his head several times in the second. The data was binned to 157 bins before optimization.

Results

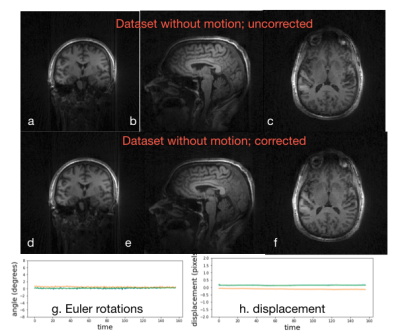
The results in Fig. 2 using the simulations show that the proposed approach is able to reliably estimate the motion parameters. The corrected image has noticeably less blurring and distortion, indicating the benefit of the corrections. The results in Fig. 3 show that the proposed correction approach is able to correct the UTE data with several motion-events. The estimated motion trajectory is observed to be piece-wise smooth in nature. The corrected image is observed to have lower blurring, compared to the reconstructions without correction. In Fig. 4, we apply the correction approach to a dataset without motion. It is observed that the motion parameters are close to zero, with no significant change in image quality.

Discussion

The simulation and experimental results show the utility of the proposed scheme in minimizing motion induced errors in 3D radial acquisitions. The proposed learning-based approach is fast and is conceptually simple; it draws upon recent advanced auto-differentiation libraries. While our focus in this abstract was on radial acquisitions, it can be generalized to other acquisition trajectories including cones or spirals.

Summary of Main Findings

The proposed approach can correct radial sequences with significant motion. The experimental results show reduced blurring and motion artifacts in UTE acquisitions.