Introduction

With the increasing use of multi-echo gradient-echo (mGRE)-based myelin water fraction (MWF) in studying demyelinating diseases, significant efforts have been made by various groups in recent years to improve the accuracy and robustness of MWF estimation^1-8. The basic MWF estimation method is based on the multi-exponentials model^5,9. Separating overlapping exponentials is a known ill-conditioned computational problem and the estimation results are often very sensitive to noise and data perturbations^8,10. To address this problem, several advanced methods have been proposed, which exploit prior information, such as spectral and spatial smoothness^5,11, nonlocal similarity¹², image sparsity⁶, and more recently deep learning-based priors^7,13, to constrain MWF estimation. This work presents a new learning-based approach to further improve MWF estimation. The proposed method uses a subspace model to represent different water components with significantly improved conditioning; it also incorporates pre-learned subspace structures, parameter distributions, and low-dimensional manifolds to further improve estimation accuracy. The proposed method has been validated using both simulation and experimental data. Our results show that the proposed method can produce significantly improved MWF estimates that are robust to noise and data perturbations.

Methods

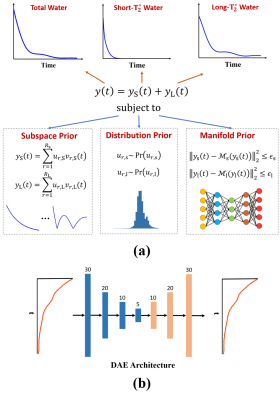
Signal Model
As illustrated in Fig. 1a, the proposed method expresses the multi-component water signal as:
$$\hspace{4em}y(t)=y_{\text{S}}(t)+y_{\text{L}}(t)\hspace{12em}\\\hspace{6.2em}=\sum_{r=1}^{R_{\text{S}}}u_{r,\text{S}}v_{r,\text{S}}(t)+\sum_{r=1}^{R_{\text{L}}}u_{r,\text{L}}v_{r,\text{L}}(t),\hspace{4em}\\\hspace{4em}\text{subject}\:\text{to}\hspace{24em}\\u_{r,\text{S}}\sim\text{Pr}\left(u_{r,\text{S}}\right),\:u_{r,\text{L}}\sim\text{Pr}\left(u_{r,\text{L}}\right)\\\hspace{15.5em}\text{and}\:\left\|y_{\text{S}}(t)-\mathcal{M}_{\text{S}}\left(y_{\text{S}}(t)\right)\right\|_2^2\leq\epsilon_{\text{S}},\:\left\|y_{\text{L}}(t)-\mathcal{M}_{\text{L}}\left(y_{\text{L}}(t)\right)\right\|_2^2\leq\epsilon_{\text{L}},\hspace{12em}(1)$$
where ‘S’ and ‘L’ denote the short-$$$\text{T}_2^{*}$$$ myelin water component and other long-$$$\text{T}_2^{*}$$$ water components, respectively. The proposed model has the following key features: a) use of low-rank subspaces to express the signals of different water components exploiting their partial separability, b) imposing statistical distributions on the subspace model coefficients (i.e., $$$\{u_{r,\text{S}}\}$$$ and $$$\{u_{r,\text{L}}\}$$$ ) to constrain the signal variations allowed, and c) enforcing the short-$$$\text{T}_2^{*}$$$ and long-$$$\text{T}_2^{*}$$$ water components to have small Euclidean distances to some nonlinear manifolds, $$$\mathcal{M}_{\text{S}}$$$ and $$$\mathcal{M}_{\text{L}}$$$, respectively.

As compared to the conventional multi-exponential model, our model is much better conditioned due to the orthogonality of the bases representing each water component. Moreover, the distribution and manifold-based priors provide effective constraints for addressing the inter-component overlapping issue.

Learning-Based MWF Estimation
In this work, we learn the subspace structures (i.e., $$$\{v_{r,\text{S}}(t)\}$$$ and $$$\{v_{r,\text{L}}(t)\}$$$) and parameter distributions (i.e., $$$\text{Pr}\left(u_{r,\text{S}}\right)$$$ and $$$\text{Pr}\left(u_{r,\text{L}}\right)$$$ ) from training data obtained in vivo (from 12 healthy volunteers). More specifically, we first fit the training data with the conventional exponential model to produce a large set of synthetic short-$$$\text{T}_2^{*}$$$ and long-$$$\text{T}_2^{*}$$$ water signals. From these synthetic signals, we then determined the basis functions through principal component analysis (PCA). Then, the corresponding subspace coefficients were estimated via least-squares fitting. The resulting coefficients from different voxels can be treated as samples drawn from the desired distributions. We parameterized the distributions as Gaussians and determined the parameters from the obtained samples under the maximum likelihood principle.

Similarly, we also learned the desired manifolds $$$\mathcal{M}_{\text{S}}$$$ and $$$\mathcal{M}_{\text{L}}$$$ from training data. Specifically, we used deep autoencoders (DAEs) to capture the manifold structures and learned the model parameters through unrolling an iterative algorithm for solving the MWF estimation problem. More specifically, based on the proposed model, we formulated the following constrained optimization problem:
$$\hspace{12em}\min_{u_{r,\text{S}},u_{r,\text{L}}}\left\|y(t)-\left(\sum_{r=1}^{R_{\text{S}}}u_{r,\text{S}}v_{r,\text{S}}(t)+\sum_{r=1}^{R_{\text{L}}}u_{r,\text{L}}v_{r,\text{L}}(t)\right)\right\|_2^2-\log\left(\text{Pr}\left(u_{r,\text{S}}\right)\right)-\log\left(\text{Pr}\left(u_{r,\text{L}}\right)\right)\hspace{18em}\\\hspace{12em}+\lambda_{\text{S}}\left\|y_{\text{S}}(t)-\mathcal{M}_{\text{S}}\left(y_{\text{S}}(t)\right)\right\|_2^2+\lambda_{\text{L}}\left\|y_{\text{L}}(t)-\mathcal{M}_{\text{L}}\left(y_{\text{L}}(t)\right)\right\|_2^2,\hspace{18em}(2)$$
which incorporates the learned subspace structures and parameter distributions. We used an iterative algorithm to solve Eq. (2) by alternating between the following steps:
$$\hspace{10em}\textbf{U}_{\textbf{S}}\textbf{-step}:z_{\text{S}}^{(n)}(t)=\mathcal{M}_{\text{S}}\left(\sum_{r=1}^{R_{\text{S}}}u_{r,\text{S}}^{(n)}v_{r,\text{S}}(t)\right)\hspace{26em}(3)\\\hspace{12em}u_{r,\text{S}}^{(n+1)}=\arg\min_{u_{r,\text{S}}}\left\|y(t)-\left(\sum_{r=1}^{R_{\text{S}}}u_{r,\text{S}}v_{r,\text{S}}(t)+\sum_{r=1}^{R_{\text{L}}}u_{r,\text{L}}^{(n)}v_{r,\text{L}}(t)\right)\right\|_2^2\hspace{12em}\\\hspace{18em}-\log\left(\text{Pr}\left(u_{r,\text{S}}\right)\right)+\lambda_{\text{S}}\left\|\sum_{r=1}^{R_{\text{S}}}u_{r,\text{S}}v_{r,\text{S}}(t)-z_{\text{S}}^{(n)}(t)\right\|_2^2\hspace{16.0em}(4)\\\hspace{10em}\textbf{U}_{\textbf{L}}\textbf{-step}:z_{\text{L}}^{(n)}(t)=\mathcal{M}_{\text{L}}\left(\sum_{r=1}^{R_{\text{L}}}u_{r,\text{L}}^{(n)}v_{r,\text{L}}(t)\right)\hspace{26em}(5)\\\hspace{12em}u_{r,\text{L}}^{(n+1)}=\arg\min_{u_{r,\text{L}}}\left\|y(t)-\left(\sum_{r=1}^{R_{\text{S}}}u_{r,\text{S}}^{(n+1)}v_{r,\text{S}}(t)+\sum_{r=1}^{R_{\text{L}}}u_{r,\text{L}}v_{r,\text{L}}(t)\right)\right\|_2^2\hspace{12em}\\\hspace{18em}-\log\left(\text{Pr}\left(u_{r,\text{L}}\right)\right)+\lambda_{\text{L}}\left\|\sum_{r=1}^{R_{\text{L}}}u_{r,\text{L}}v_{r,\text{L}}(t)-z_{\text{L}}^{(n)}(t)\right\|_2^2.\hspace{15.5em}(6)$$
Since $$$\text{Pr}\left(u_{r,\text{S}}\right)$$$ and $$$\text{Pr}\left(u_{r,\text{L}}\right)$$$ are parameterized as Gaussians, Eq. (4) and Eq. (5) reduce to linear least squares problems that have close-form solutions. By unrolling Eqs. (3-6), we can train the DAE models in an end-to-end fashion. In this work, each DAE was implemented as a 7-layer fully-connected network with a bottleneck architecture (Fig. 1b). 300k synthetic data were used for network training, generated based on the conventional exponential model with parameters determined from in vivo data.

With all the priors learned from training data, MWF estimation was done through the constrained optimization problem in Eq. (2), which produced the estimates of $$$\hat{u}_{r,\text{S}}$$$ and $$$\hat{u}_{r,\text{L}}$$$. The final MWF value was then calculated as $$$\left\{\sum_{r=1}^{R_{\text{S}}}\hat{u}_{r,\text{S}}v_{r,\text{S}}(0)\right\}/\left\{\sum_{r=1}^{R_{\text{S}}}\hat{u}_{r,\text{S}}v_{r,\text{S}}(0)+\sum_{r=1}^{R_{\text{L}}}\hat{u}_{r,\text{L}}v_{r,\text{L}}(0)\right\}$$$.

Results

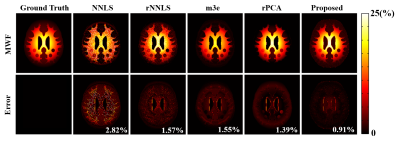
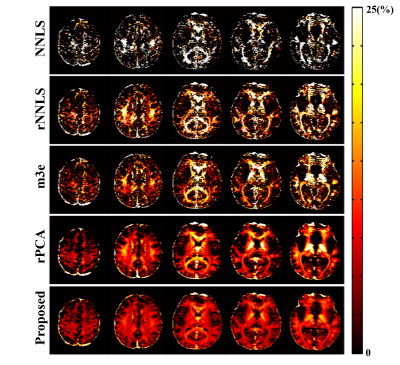
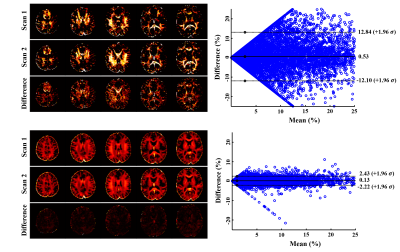
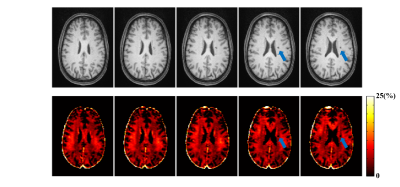
The proposed method has been evaluated using both simulated and in vivo experimental data. In the simulation study, a numerical phantom was generated with parameter values from the literature. We compared the proposed method with several existing fitting schemes, including the recently proposed robust PCA-based scheme². As can be seen in Fig. 2, our method achieved the best performance with significantly improved accuracy. In our in vivo experiments, mGRE images were acquired on a 3T scanner. Figure 3 shows the results from one healthy subject. As can be seen, the proposed method showed superior performance to the existing schemes, with reduced noise-induced fluctuations and susceptibility-induced artifacts. We also evaluated the reproducibility through repeated scans. As shown in Fig. 4, the proposed method achieved significantly reduced inter-scan variations than the conventional method. The proposed method has also been applied to data acquired from one tumor patient with a small lesion. As shown in Fig. 5, our method successfully captured the focal demyelination within the lesion area.

Conclusions

We present a novel learning-based method to address the ill-conditionedness problem associated with MWF estimation by synergistically integrating pre-learned subspace structures, statistical distributions, and nonlinear manifolds. Our method has been validated using both simulated and experimental data, producing encouraging results. The proposed method may further improve the practical utility of quantitative myelin imaging in clinical settings.

Acknowledgements

This work reported in this paper was supported, in part, by NIH-R21-EB023413.