4469
Tetrahedral based Method for Intracranial Blood Vessels Volume Calculation1Center for Biomedical Imaging Research, Tsinghua University, Beijing, China
Synopsis
The rupture of intracranial atherosclerotic plaque is a major cause of ischemic stroke. The atherosclerotic plaque burden was proposed to measure the risk of plaque vulnerability, which can be quantified by the volume of the vessel wall calculated on MR images. However, due to the complex shape of intracranial blood vessels, the traditional calculation method may reduce the accuracy of plaque burden measurement,especially overlapped in the curved vessels. Therefore, a tetrahedral based method was proposed to reduce the volume calculation error of intracranial vessel wall. The proposed method was validated in simulation and in-vivo datasets.
Introduction
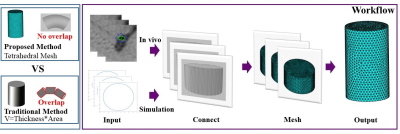
Intracranial atherosclerotic disease (ICAD) is a major cause of ischemic stroke worldwide and an important public health concern globally1-5. The rupture of intracranial atherosclerotic plaque is a major cause of ischemic stroke. The atherosclerotic plaque burden was proposed to measure the risk of plaque vulnerability6, which can be quantified by the volume of the vessel wall calculated on MR images. However, due to the large curvature of intracranial blood vessels, the traditional calculation method, i.e., image slice thickness multiplies the vessel area, may cause the overlap when the slice thickness is larger than the radius of curvature, thus reducing the accuracy of plaque burden measurement. Therefore, in this study a tetrahedral based method was proposed to reduce the volume calculation error by reconstructing the vessel into lots of small tetrahedron and summing the volume of them. The performance of the proposed method was validated in simulation and in-vivo datasets.Method
Volume CalculationIn the traditional volume calculation method, the central line of the vessel was first obtained, and then the lumen and outer wall of the vessel were delineated with a series of points in the vessel cross-section. The vessel area can be calculated using these delineated points. Finally, the vessel volume was obtained by multiplying the vessel area in the cross-section and the slice thickness7-9. After getting the delineated points, order f(v) represents the connection function of two adjacent blood vessel:
$${\rm{F}} = \mathop{{\int\!\!\!\!\!\int\!\!\!\!\!\int}\mkern-31.2mu \bigodot}\nolimits_\Omega {f(v)dV} $$
$$v \in \Omega ,Bv = g$$
v is the boundary control point delineating the vascular region, Ω is the set of control points , g is the boundary function for the two adjacent slices. The solution of F with respect to the boundary condition g can be solved by partial differential equations. Finite element analysis is often used to solve discrete partial differential equations10. Finite element method divides the computational domain into finite non-overlapping elements, and select some appropriate nodes as interpolation points of the solution function in each element. In three dimensions, F can be expressed as the sum of the volumes of the tetrahedron. The whole workflow as shown in FIG.1.
Simulation and In-vivo Experiments
The simulation experiment was performed to validate the proposed method (Fig. 2). We designed the different regular shapes (Sim. a and b) to simulate the vessel lumen and outer wall, which the volume can be calculated analytically as the golden standard. Furthermore, we simulated some vessels under different stenosis conditions (Sim. c and d).
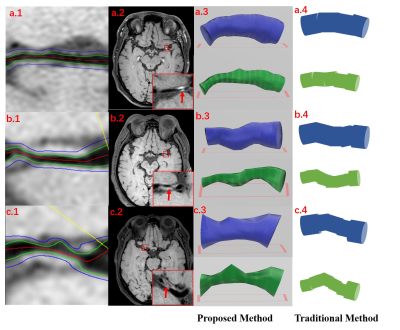
In the in-vivo experiment, with the approval of institutional review board, three patients with intracranial arterial stenosis underwent the black-blood T1-weighted VISTA (volume isotropic turbo spin echo acquisition, VISTA) sequence with the spatial resolution of 0.6 mm isotropic on a 3T scanner (Achieva CX, Philips Healthcare, The Netherlands). For each subject, lumen and outer wall were outlined manually on the vessel cross-sections using an in-house software.
Results
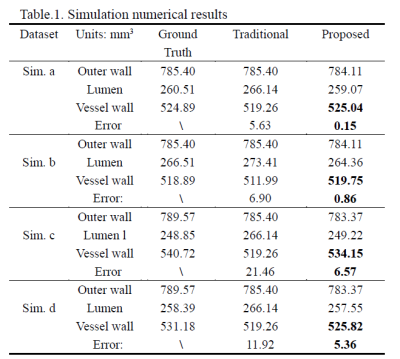
As shown in Table 1, in simulation dataset the proposed method achieved less volume calculation error than the traditional methods in regular shapes (Sim. a-b). In practice, the shape of intracranial blood vessels is more complex, so we took more attention to the simulation of curved blood vessels. The proposed method still had less errors than the traditional method (Sim. c-d).In in-vivo experiment, the proposed method can accurately reconstruct the shape of intracranial blood vessels. Reconstructed vessel lumen and outer walls are shown in Fig.3. Visually, the result of the traditional method was the rough approximation for the real condition, while the proposed method can reflect the shape of real blood vessels.
Quantitative results of in-vivo datasets are shown in Table 2. The volume of lumen showed the larger difference between two methods, thus resulting in the vessel wall volume calculation.
Discussion and Conclusions
A novel tetrahedral based volume calculation method was introduced. The proposed approach has an improved accuracy for vessel wall volume calculation, validated in the simulation and in-vivo datasets.Acknowledgements
NoneReferences
1. Go A . Executive Summary: Heart Disease and Stroke Statistics—2013 Update: A Report From the American Heart Association[J]. Circulation, 2015, 127.
2. Lusis A J . Atherosclerosis. Nature[J]. Nature, 2000, 407(6801):233-241.
3. Kerwin, William S . Carotid Artery Disease and Stroke: Assessing Risk with Vessel Wall MRI[J]. Isrn Cardiology, 2012, 2012:180710.
4. Nascet C . Beneficial effect of carotid endarterectomy in symptomatic patients with high-grade carotid stenosis[J]. N Engl J Med, 1991, 325.
5. None. Clinical advisory: carotid endarterectomy for patients with asymptomatic internal carotid artery stenosis.[J]. Stroke; a journal of cerebral circulation, 1994, 25(12):2523-4.
6. Falk E. Why do plaques rupture?[J]. Circulation, 1993, 86(6 Suppl):III30-42.
7. Mi S, Gao P , Qian Z , et al. Middle Cerebral Artery Atherosclerosis and Deep Subcortical Infarction: A 3T Magnetic Resonance Vessel Wall Imaging Study[J]. Journal of Stroke & Cerebrovascular Diseases, 2018.
8. Kang X, Polissar N L , Chao H , et al. Analysis of the measurement precision of arterial lumen and wall areas using high-resolution MRI.[J]. Magnetic Resonance in Medicine Official Journal of the Society of Magnetic Resonance in Medicine, 2015, 44(6):968-972.
9. SR* †, JC †, RT †, et al. An Ex Vivo Evaluation of Tomographic 3-D Ultrasound, B-Mode Ultrasound, CT And MR Imaging to Measure Artery Diameter, Length and Wall Volume[J]. Ultrasound in Medicine & Biology, 2019, 45(10):2819-2829.
10. Williamson, M. P. Finite-element analysis[J]. Computer-Aided Engineering Journal, 1985, 2(2):66-69.
Figures