Introduction

The sodium triple-quantum (TQ) signal represents a unique intracellular sensitive biomarker for cell viability due to its intrinsic selectivity to interactions of sodium ions with proteins. To separate the TQ coherence from other coherences phase cycled pulse sequences, such as the TQ time proportional phase incrementation (TQTPPI) sequence¹, are used. The acquired signal is a combination of various coherences from multiple relaxation pathways, which complicates the signal interpretation. Hence, a simulation framework of spin-3/2, sodium, NMR dynamics provides a unique tool to characterize/quantify the signal components. Simulation frameworks for sodium NMR pulse sequences have been already proposed^2-5. However, these simulation frameworks are not optimized for fast computation of arbitrary phase cycles with multiple iterations and varying time delays.

In this study, we present a computationally efficient modular simulation framework for spin-3/2, sodium, NMR dynamics in biological environments and under hard RF pulses. This simulation framework provides a complete description of all signal components for arbitrary pulse sequences. Hence, pulse sequences can be optimized and the influence of sequence and probe parameters on the signal can be quantitatively evaluated. The performance of the simulation framework was compared with measurement data using TQTPPI pulse sequence and sodium nuclei.

Methods

The dynamics of spin-3/2 nuclei are described by the Liouville-equation
$$\frac{d\sigma}{dt}=-i\left[H,\sigma\right],$$ where $$$H$$$ is the Hamiltonian of the system under study and the density operator $$$\sigma$$$ is expressed in terms of irreducible spherical tensor operators $$$T_{mn}$$$ (ISTOs).

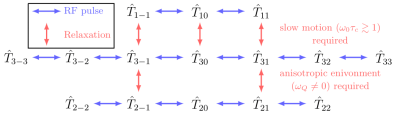
In the following, an overview of the effect of hard RF pulses and relaxation is given. For a detailed description, see e.g.^5-8. Fig.2 summarizes the allowed transitions for relaxation and hard RF pulses.

The effect of hard pulses with flip angle $$$\theta$$$ and phase $$$\phi$$$ on the ISTOs follows the equation
$$\hat{P}(\theta,\phi)T_{mn} = \sum\limits_{n'}{e^{i(n'-n)\phi}d^m_{n'n}(\theta)T_{mn'}}$$
with the Wigner matrix elements $$$d^m_{n'n}(\theta)$$$. Each change in coherence order results in a different sensitivity to the RF pulse phase. Multi-quantum (MQ) pulse sequences exploit this to separate different coherence orders.

The quadrupole interaction dominates the relaxation of quadrupole nuclei and follows the equation
$$ \frac{d\sigma}{dt}=-i\bar{\omega}_Q\left[T_{20},\sigma\right]-\sum\limits^2_{n=-2}{\left[T_{2n},\left[T_{2n}^\dagger,\sigma-\sigma_\text{eq}\right]\right]\left(J_n(\omega_0)+iK_n(\omega_0)\right)}$$
which yields a set of decoupled differential equations, shown in Fig.1. Off-diagonal terms correspond to the formation of MQ coherences. In an isotropic environment, i.e. $$$\bar{\omega}_Q=0$$$, all $$$T_{2n}$$$ tensors decouple from the other tensors. Solving the differential equations leads to transition equations $$$T_{mn}\rightarrow\sum_{m'}{f^{(n)}_{m'm}(t)T_{m'n}}$$$ in arrow notation, where $$$f^{(n)}_{m'm}(t)$$$ are the transfer functions. In the slow motion regime, i.e. $$$\omega_0\tau_c\gtrsim1$$$, the $$$f^{(n)}_{m'm}(t)$$$ are bi-exponential. The relevant transfer functions for transversal relaxation pathways in isotropic environment are
$$
f^{(1)}_{11}(t)=\frac{1}{5}\left(3\exp\left(-\frac{t}{T_{2f}}\right)+2\exp\left(-\frac{t}{T_{2s}}\right)\right)\\ f^{(1)}_{13}(t)=f^{(1)}_{31}(t)=\frac{\sqrt{6}}{5}\left(\exp\left(-\frac{t}{T_{2f}}\right)-\exp\left(-\frac{t}{T_{2s}}\right)\right)\\ f^{(1)}_{33}(t)=\frac{1}{5}\left(2\exp\left(-\frac{t}{T_{2f}}\right)+3\exp\left(-\frac{t}{T_{2s}}\right)\right)
$$
with relaxation rates $$$\frac{1}{T_{2f}}=J_0+J_1$$$ (fast), $$$\frac{1}{T_{2s}}=J_1+J_2$$$ (slow). Here, $$$J_n=\omega^2_Q\cdot\frac{\tau_c}{1+(m\tau_c\omega_0)^2}$$$ are the spectral densities with the correlation time $$$\tau_c$$$ and the quadrupole interaction strength $$$\omega_Q$$$, which are empirically parameters that together fully describe the system under investigation. The formation of TQ coherences requires a slow motion regime $$$\omega_0\tau_c\gtrsim1$$$ causing biexponential relaxation.

The described formulation provides a computational efficient treatment of quadrupolar NMR dynamics under the separated effect of relaxation and hard RF pulses. Hence, a complete simulation framework of arbitrary pulse sequences containing various RF pulses and relaxation periods can be performed.

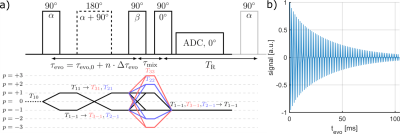
To evaluate the performance of the simulation framework, the signal dynamics between simulated and measured data was compared using the TQTPPI pulse sequence¹ (Fig.3). Measurements were performed at a 9.4T preclinical MRI (Bruker Biospec94/20) equipped with a linear ¹H/²³Na Bruker volume coil. The sample contained 154mM NaCl and [2,4,6]%w/w agarose phantom embedded into a larger phantom to minimize inhomogeneity. The TQTPPI FID was non-linearly fitted using¹:
$$Y(t)=\sin(\omega t+\phi_1)\cdot\left(A_{SQ,1}e^{-t/T_{2f}}+A_{SQ,2}e^{-t/T_{2s}}\right)+A_{TQ}\sin(3\omega t+\phi_2)\left(e^{-t/T_{2f}}-e^{-t/T_{2s}}\right)+DC$$
where $$$Y(t)$$$ is the TQTPPI FID amplitude and, $$$A_{SQ,i}$$$ and $$$A_{TQ}$$$ are the SQ and TQ amplitudes, respectively.

Results/Discussion

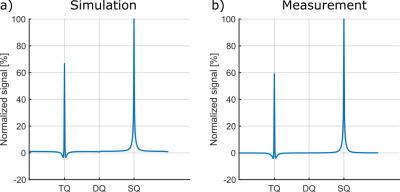
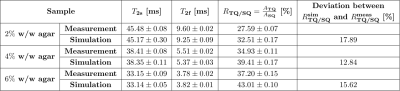
Fig.4 shows exemplary simulated and measured TQTPPI spectra using a sample containing 4%w/w agarose and 154mM NaCl. Tab.1 lists the fit results of simulated and measured data for all samples. The relaxation times of simulated data yielded a good agreement with measurement data, while the TQ/SQ ratio deviated less than 20%. The reasons for this deviation are $$$B_0$$$ and $$$B_1$$$-inhomogeneities, which are not accounted for in the simulation. $$$B_0$$$-inhomogeneity adds auto-relaxation terms to the differential equation shown in Fig.1 and therefore reduces the TQ signal, while $$$B_1$$$-inhomogneity also causes a loss of TQ signal due to a $$$\sin^5(\theta)$$$ flip angle dependence of the TQ signal. The simulation framework can account for $$$B_0$$$ and $$$B_1$$$-inhomogeneities using $$$B_0$$$ and $$$B_1$$$-maps. The excellent agreement between simulated and measured data demonstrated that the system under study is completely described by $$$\tau_c$$$ and $$$\omega_Q$$$.

The computationally efficient modular simulation framework opens the field for novel pulse sequences, improved signal suppression methods and unique phase cycles. Furthermore, quantitative parameter studies of pulse sequence and sample parameters can be performed without the need for lengthy measurements. This allows to obtain a deeper understanding of the influence of specific parameters on the signal.

Conclusion

To obtain a deeper understaning of physical parameters affecting the signal of arbitrary quadrupolar NMR pulse sequences, we present a flexible and modular simulation framework for quadrupolar NMR dynamics. Comparison between simulated and measured data showed excellent agreement using TQTPPI pulse sequence. Hence, the influence of sample and pulse sequence parameters on quadrupole NMR signals of arbitrary pulse sequences can be easily evaluated.

Acknowledgements

No acknowledgement found.