PURPOSE

It has previously been shown that spin-lock sequences with low locking amplitudes (ω₁) can reduce the losses caused by diffusion in regions containing susceptibility inhomogeneities. Judicious selection of locking powers and combinations of data acquired with different ω₁ can isolate susceptibility effects from other influences on signal losses, and may be used to quantify the spatial frequencies of intrinsic susceptibility gradients. In tissues these are likely dominated by microvasculature ^1-3. Breathing oxygen causes vasoconstriction in the brain, and detection of the effects of breathing gas challenges may be useful for assessing cerebrovascular integrity. Previously, vessel size imaging by MRI has been based on comparing gradient-echo (GE) and spin-echo (SE) signals after injection of a paramagnetic contrast agent ^{4, 5}. We evaluated the capability of spin-lock imaging with low locking amplitudes to detect changes of vessel diameter caused by breathing oxygen.

METHODS

Spin-lock experiments were performed on a 4.7T Varian animal system. A spin-lock preparation cluster (90_x-τ_y/2-180_y-τ_-y/2-90_x) was applied before single-shot spin-echo EPI readouts. R_1𝞀 values were obtained by acquiring images with spin-lock times (SLT) varying as 1, 5, 10, 15, 20, 25, 50, 75, 100 ms. Values of R_1𝞀 were obtained by fitting the spin-locking signal (S) with a mono-exponential function S/S₀ = exp(-R_1𝞀﹒SLT), in which S₀ is the signal measured with SLT of 0 ms. R_1𝞀 values at different fields (= R_1𝞀 dispersion) were obtained by varying ω₁ from 0 Hz to 10 kHz. All images were acquired with matrix size 64 × 64, FOV = 30 ×30 mm, and a single-slice scan with slice thickness of 2 mm.
All animal procedures were approved by the local Animal Care and Usage Committee. All rats were immobilized and anesthetized with 2-3% isoflurane (ISO) and lab air before MR imaging. Four healthy rats with first intake of air and then 97-98% O2 were scanned. Respiration rate was monitored to be in a range from 40 to 70 breaths per minute. Rectal temperature was maintained at 37°C using a warm-air feedback system.
When ω₁ is weak errors in the quantification of R_1𝞀 arise because of B₀ variations that introduce off-resonance effects. Previously, we have described a data correction which can reduce this error when the B₀ shift is not too large ⁶. To use this correction, B₀ and B₁ maps were measured. B₀ maps were obtained from two images acquired with a GE sequence with TEs of 5 ms and 8 ms, TR of 30 ms, and flip angle of 20º. B₁ maps were obtained by a double-angle approach using two images acquired with a GE sequence with excitation flip angles of 60º and 120º, TR of 2 s, and TE of 10 ms.

R1ρ in biological tissues can be expressed as the superposition of R_1ρ^Diff, R_1ρ^Ex, and R_2a ^{1, 2},
$$ R_{1ρ}=R_{1ρ}^{Diff}+R_{1ρ}^{Ex}+R_{2a} $$ (1)
where R_1ρ^Diff and R_1ρ^Ex are the relaxation rates due to water diffusion through susceptibility gradients and chemical exchange effects, respectively. R_2a is the intrinsic transverse relaxation rate. The contribution to R_1ρ^Diff from water with self-diffusion coefficient D is given by ^1-3
$$ R_{1ρ}^{Diff}=γ^2 g^2 D/((q^2 D)^2+ω_1^2 ) $$ (2)
where q represents an effective spatial frequency that characterizes the scale of the inhomogeneities, and g is the mean gradient strength. R, the scale of the inhomogeneities producing the gradients, can then be estimated as ≈ π/q. R_1ρ^Ex + R_2a can be regarded as constant (c) over a range of low ω₁, so q in biological tissues can be obtained by using Equations 1 and 2. Here, q values were obtained by fitting R_1𝞀 acquired with ω₁ of 0, 56, 100, 177, and 316 Hz so any dispersion is mainly due to diffusion effects.
Maps of R_1𝞀 and R were calculated voxel-wise but voxels with B₀ shift > 20 Hz were omitted. Similarly, voxels indicating R values > 15 µm were also omitted as they corresponded to low SNR.

RESULTS

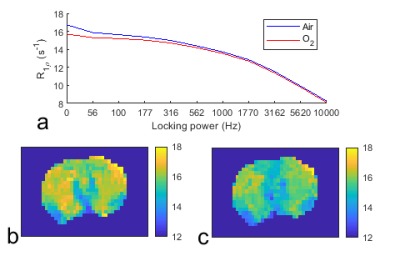
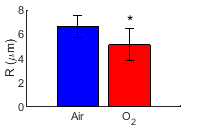
Fig. 1a shows the average of the corrected R_1𝞀 dispersions acquired with intake of air and O₂, respectively. Note that R_1𝞀 values with low ω₁, but not high ω₁, decrease after the intake of O₂, suggesting that the oxygen challenge changes the intrinsic susceptibility but not chemical exchange or intrinsic transverse relaxation. Fig. 1b and 1c show the corrected R_1𝞀 maps with ω₁ of 100 Hz acquired with intake of air and O₂, respectively, from a representative rat brain. Fig. 2 shows the statistical analysis of R values from the whole brain acquired with intake of air and O₂, respectively. Note that R values significantly decrease after the intake of O₂. R values with intake of air and O₂ were estimated to be 6.6 ± 0.9 µm and 5.1 ± 1.3 µm, respectively (assuming D = 2×10^-5 cm²s^-1), which are roughly in agreement with a previous report ⁵.

DISCUSSION AND CONCLUSION

Spin-lock dispersion imaging with low locking amplitudes and appropriate data corrections may be an alternative method for vessel size imaging and does not require contrast agent.

Acknowledgements

The authors acknowledge grant support from NIH (R01 EB024525)