4408
Comprehensive 3D quantitative transient response MRI1Radiology and Nuclear Medicine, Erasmus MC, Rotterdam, Netherlands, 2GE Healthcare, Hoevelaken, Netherlands
Synopsis
Unlike multi-parametric methods as MR Fingerprinting and quantitative transient imaging we present a quantitative MRI method based on the transient response without variation of experimental parameters (FA…). Our method is based on the exact solution of the recursive equation for the magnetization along an acquisition train. Based on this analytical approach we determine the requirements for the features and parameters of a repeated acquisition block to allow simultaneous estimation of experimental (B0, B1) and intrinsic (PD, T1, T2) parameters. The feasibility of the technique on clinical scanners is demonstrated by acquiring a comprehensive set of 3D in vivo parametric maps.
Introduction
Several transient-response-based quantitative methods were proposed in recent years1,2. These methods rely on specific variation of acquisition parameters such as excitation flip angle and repetition time along the train of excitation pulses. With such variations, the time dependent Bloch equation, as well as its discretized version describing the signal evolution in an acquisition train, do not have a closed-form analytical solution. Hence, these methods have to resort to iterative forward modeling or dictionary matching for parameter estimation and sequence optimization. In contrast to these methods, we propose a constant propagator (defined as the cumulative effect of the acquisition block on the magnetization as a linear operator) along the echo train in order to enable an exact analytical description of the signal3. The explicit analytical expression of the signal evolution reveals critical conceptual elements in the experimental design: 1) enhance or suppress sensitivity to intrinsic and experimental parameters; 2) avoid potential loss of information in the signal evolution; and 3) species can be identified by their unique signal behaviour. We demonstrate this design process of the propagator, that ultimately allows a comprehensive parameter estimation in the transient phase, including experimental confounding quantities such as B0 and B1. We propose a novel, balanced free precession sequence that avoids banding artefacts. We demonstrate the method’s sensitivity to intrinsic and experimental parameters with phantoms and the its applicability of the technique in the clinical settings by 3D in vivo acquisition and parameter estimation.Methods
Theoretical foundationsWe describe the evolution of the magnetisation mn for a species characterised by intrinsic and experimental parameters with the Putzer's algorithm4,5. This allows an analytical and always real-valued expression for μn = mn - msteady state without the diagonalization of the propagator6,7, instead using its eigenvalues and avoiding its often complex eigenvectors:
μn = ρn·sin(nφ)·n1 + ρn·cos(nφ)·n2 + ηn·n3 ,
where the real-valued normal mode (not eigenvectors) vectors are determined by the initial state, the propagator and the eigenvalues ρ·eiφ, ρ·eiφ and η. A generally valid expression for the signal in the quadrature complex notation follows:
sn = a·ρn·ei(nφ+δ) + b·ηn·eiξ
Propagator design for parametric mapping
The goal of the propagator design in parametric mapping is to produce a signal evolution that allows parameter estimation. There are three main aspects to consider: 1. The effect of B0 inhomogeneity is suppressed; 2. The signal evolution carries full information; 3. Species can be identified by their unique signal evolution. Our choice of for a propagator that satisfies these requirements consists of four excitations with alternating phases 0, π/2, π/2, 0 with flip angles 30, 175, 30, 175 degrees. Requirement 2. is provided by the different phases in the excitation scheme. Requirements 1. and 3. are explained and demonstrated in Kotek et al.3.
Implementation on a clinical scanner, acquisition and parameter estimation
The acquisition was done in-vivo and on a phantom (CaliberMRI System Phantom Lite) by 3D stack of spirals balanced GRE: 22 slices, 6mm thickness, stack of spirals: 32 arms, 1024 readout points, FoV 25 and 30 for in-vivo and phantom acquisition. Image reconstruction was done with a non-uniform FFT with density compensation8, and parameter estimation through the least-squares fitting of the single-species signal model.
Results
The in vivo parametric maps produced with our design are depicted in Figure 1. The T2 values are in good agreement of literature references, while the T1 maps show systematic underestimation of T1. In contrast with the in vivo results, results from phantoms show good agreement between our derived T1 and T2 and reference values as shown in Figure 2 and 3.Discussion
We approached transient state quantitative imaging from a simple algebraic perspective. We challenged the necessity of flip angle or repetition time variation. We investigated if in the case of a constant propagator the signal evolution contains sufficient and exploitable information about intrinsic and experimental parameters. This is the only obvious case when there is a closed-form analytical solution to the Bloch equation. We identified conceptual requirements for the propagator through simple algebraic considerations. The design concept resulted in the following: 1. a novel balanced free precession technique that produces banding artefact free transient state and steady state images; 2. A comprehensive set of parametric maps: T1, T2, PD, B0, B1. Here we focus mainly on the conceptual details of our method and its direct implementation. For applicability in a clinical workflow further steps are necessary towards acceleration of the acquisition. Furthermore, the underestimation of T1 from in vivo data requires further investigation to find confounding biologically relevant processes. The technique can be developed further where such processes are enhanced or suppressed by the design of the propagator.Conclusion
The analytical description provided insight to a proper experimental design that otherwise was not obvious or available when a simulation-based optimization is performed. Among transient state quantitative imaging methods, conceptually and also technically the simplest case is with constant propagator (the one of two cases with analytical solution). Here we demonstrated with an implementation in clinical settings, that no variation of the experimental parameters is necessary in multi-parametric transient response imaging.Acknowledgements
This work was supported partially by GE Healthcare (Work statements: B-GEHC-8-2018 and B-GEHC-10_SETI II).References
1. Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature. 2013;495(7440):187-192.
2. Gómez, P. A., Molina-Romero, M., Buonincontri, G., Menzel, M. I. & Menze, B. H. Designing contrasts for rapid, simultaneous parameter quantification and flow visualization with quantitative transient-state imaging. Sci. Rep. 9(1), 8468 (2019)
3. Kotek, G., Nunez-Gonzalez, L., Vogel, M. W., Krestin, G. P., Poot, D., & Hernandez-Tamames, J. A. (2021). From signal-based to comprehensive magnetic resonance imaging. Scientific reports, 11(1), 17216.
4. Elaydi,S.N. An Introduction To Difference Equation (Springer,2020)
5. Putzer, E. J. Avoiding the Jordan canonical form in the discussion of linear systems with constant coefficients. Am. Math. Mon. 73(1), 2–7 (1966).
6. Hargreaves, B. A., Vasanawala, S. S., Pauly, J. M., & Nishimura, D. G. (2001). Characterization and reduction of the transient response in steady-state MR imaging. Magnetic resonance in medicine, 46(1), 149–158.
7. Ganter C. (2004). Off-resonance effects in the transient response of SSFP sequences. Magnetic resonance in medicine, 52(2), 368–375.
8. Pruessmann, K. P., Weiger, M., Börnert, P., & Boesiger, P. (2001). Advances in sensitivity encoding with arbitrary k-space trajectories. Magnetic resonance in medicine, 46(4), 638–651.
Figures
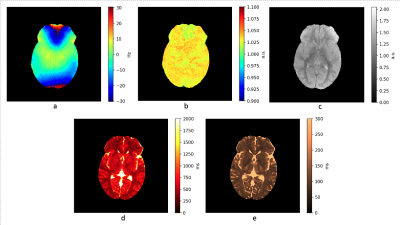
Figure 1.
In vivo parametric maps from volunteer data. Acquisition parameters: 24 channel head coil, 30x-175y-30y-175x scheme, TR=17ms, 6.3mm slice thickness, 22 slices, FoV = 25 cm, bw = 125, acquisition train length 60, 32 spiral arms, 1024 readout points per arm. Despite the fully balanced free precession acquisition sequence, no banding artefacts are present due to the composite operator consisting of excitations along various axes. The T1 and T2 maps are free of B0 or B 1 inaccuracies.
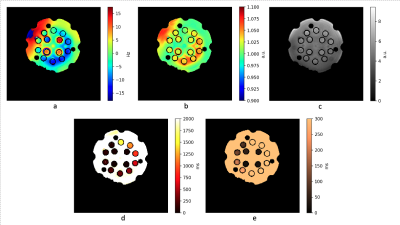
Figure 2.
Parametric maps with the Calibre System Phantom Lite - T1 contrast layer. Acquisition parameters are the same as in the in vivo acquisition except the FoV = 30 cm. The B1 map shows a similar pattern to the B0 map, emphasized only by the fine scale of the colormap. The ringing pattern on the PD map is due to the limited resolution of the acquisition. Despite the usual strong B0 inhomogeneity in the frontal area, it shows only a minor effect on PD, T1 and T2 maps. Despite showing good contrast in vivo, the T1 values are systematically underestimated.
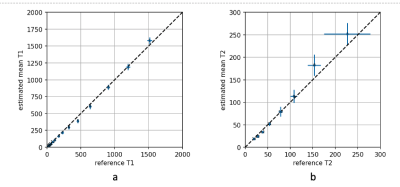
Figure 3.
The proposed method’s T1 and T2 values of the Calibre System Phantom Lite are compared to the reference values. The reference values were determined by standard inversion recovery and echo time variation SE methods. The numbers indicate the phantom’s samples. Both T1 and T2 values are in good agreement with the reference values. Unlike in the in vivo results, T1 is not underestimated.