4402
Accelerated MR Parameter Mapping with Scan-specific Unsupervised Networks1Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 2Radiology, Harvard Medical School, Boston, MA, United States, 3Biomedical Engineering, The University of Texas at Austin, Austin, TX, United States, 4Harvard/MIT Health Sciences and Technology, Cambridge, MA, United States
Synopsis
We introduce a novel framework that jointly performs advanced image reconstruction and model-based MR parameter mapping, where various traditional and modern reconstruction techniques and signal relaxation models (T1, T2, T2*, etc) can be integrated as a plug-and-play manner. Using the proposed framework, we also incorporated model-based parameter mapping with scan-specific deep learning reconstruction (a method named LORAKI). The experiment results with T2, T2* and T1 indicate that this synergistic combination is advantageous, providing improved quantitative imaging over existing methods, e.g. with up to 3.6-fold, 1.7-fold, 2.3-fold NRMSE gain in T2, T2* and T1 estimation, respectively.
Introduction
There have been many approaches to accelerated MR parameter mapping; one venue is “reconstruction-based” methods (1–6) that performs joint reconstruction of the multi-contrast data, then estimates the tissue parameters by matching predefined dictionaries or conducting (nonlinear) least-squares fitting. “Model-based” methods constitute an alternative way (7–13) by incorporating signal relaxation model (e.g. T1, T2, T2*) into the parallel imaging forward model and solving the corresponding nonlinear inverse problem. More recently, estimation with large-scale deep neural networks (14–17) has become popular, presenting improved performance with fast inference when appropriately trained. However, they often require large datasets with long training time, and may not readily generalize to different acquisition settings (e.g. relaxation types, tissue types, sampling trajectories, pathology).The goal of this work is to synergistically combine reconstruction- and model-based methods, while avoiding drawbacks of large-scale networks by utilizing physics-guided scan-specific unsupervised networks that can smoothly adjust to a specific dataset of interest without requiring a large database. We first propose a general framework that can jointly optimize the reconstruction- and model-based techniques, then embed a physics-guided scan-specific unsupervised network into this framework for improved MR parameter estimation.
Theory and Methods
Fig.1. describes the proposed framework for T2 mapping as an example. (from the top left to the right) From the undersampled k-space, it takes reconstruction to recover multi-contrast images. (From the bottom right) Together, synthetic images are generated from the MR parameters M0 and T2. By comparing those two images, it forms the Loss1 (similar to reconstruction-based approaches). Then, the synthetic images go through the forward model A consisting of coil sensitivities, Fourier transform and undersampling, to synthesize an undersampled k-space which is then matched to the original undersampled data to create Loss2 (analogous to the model-based methods). There is the third loss (LossR) for training the reconstruction method, which is only necessary for learning-based reconstruction techniques. The total loss is the summation of them to jointly optimize for the M0 and T2 parameters as well as the θ parameter (if exists) for MRI reconstruction. It is a general framework that can be used as a plug-and-play manner, where it can exploit various conventional and advanced reconstruction methods and signal models (T1, T2, T2*, etc), respectively.Among many reconstruction techniques, we showcase a recent physics-guided scan-specific unsupervised network, LORAKI (18,19), for improved parameter estimation with convenient adaptation to various data acquisition settings. As shown in Fig. 2, the network is composed of the data consistency and the regularization by the convolutional layers with the nonlinear ReLU conducted in k-space, and performs multiple unrolled conjugate-gradient iterations (18,19). As the convolution is taken within the multi-echo data, it can exploit the correlation between them (20).
The proposed framework was implemented in PyTorch with Adam optimizer for the optimization.
For evaluation, we first acquired a fully sampled in-vivo 6-echo T2 dataset from a Siemens scanner using a 12-channel head-coil, FOV=180mmx240mm, matrix size=208x256, TR=3.11s, first TE=23ms and ΔTE=34.5ms. We used the following T2-relaxation model, (for each voxel)$$s_{\mathbf{M}_0, \mathbf{T}_2}(TE) = \mathbf{M}_0 exp(-TE/\mathbf{T}_2),$$ with $$$\mathbf{M}_0 \in \mathbb{C}, \mathbf{T}_2\in\mathbb{R}$$$. The second dataset is in-vivo 7-echo T2* GRE from a Siemens scanner with a 32-channel head-coil, then coil-compressed into 16 channels. It has matrix size=224x210, resolution=1mmx1mmx2mm, TR=46ms, FA=25°, first TE=4.2ms and ΔTE=6.15ms. The signal model for T2* was$$s_{\mathbf{M}_0,\mathbf{T}_2^*,\Delta\mathbf{f}}(TE)=\mathbf{M}_0exp(-TE/{\mathbf{T}_2^*}) exp(i2\pi\Delta\mathbf{f}\cdot TE),$$ for $$$\mathbf{M}_0\in\mathbb{C}, \mathbf{T}_2^*\in\mathbb{R}$$$ with an additional phase $$$\Delta\mathbf{f}\in\mathbb{R}$$$ from magnetic field inhomogeneities. The third dataset is variable flip angle (VFA) T1 from a Siemens scanner with a 32-channel head-coil (then coil-compressed into 16 channels), with matrix=224x224, resolution=1mmx1mmx2mm, flip angles=4°, 8°, 18°, TR=7.6ms, TE=3.4ms. The signal model is$$s_{\mathbf{M}_0,\mathbf{T}_1}(\alpha)=\mathbf{M}_0sin(\alpha)\frac{1-exp(-TR/{\mathbf{T}_1})}{1-cos(\alpha)exp(-TR/{\mathbf{T}_1})}exp(i\phi_{est}),$$ with $$$\mathbf{M}_0\in \mathbb{C}, \mathbf{T}_1\in\mathbb{R}$$$ and we employed an estimated phase $$$\phi_{est}$$$ from each reconstruction to compensate for model mismatches in phase.
The comparison was conducted between reconstruction-based only, model-based only, and the proposed framework coupling them. The reconstruction methods used for the experiment were SENSE (21), SENSE with joint total variation (SENSE-JTV) (22), SENSE with joint multi-contrast LORAKS (J-LORAKS) (20,23), and LORAKI (18,19).
Results
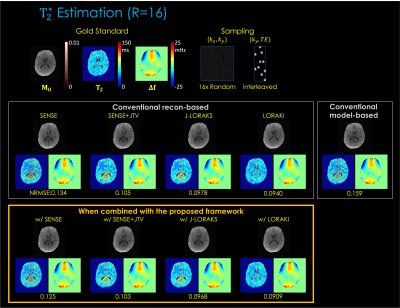
Fig. 3. shows T2 estimation from 1D R=5x uniform undersampling. The results indicate that, compared to reconstruction-based only or model-based only, the proposed framework provides improved parameter estimation. Among the multiple reconstruction methods, LORAKI presented the lowest NRMSE error, with up to 3.6- and 1.3-fold improvement in NRMSE over reconstruction- and model-based approaches, respectively.Fig. 4. displays T2* estimation using 2D R=16x random undersampling. The results are consistent, with up to 1.5- and 1.7-fold improvement in NRMSE over reconstruction- and model-based approaches, respectively.
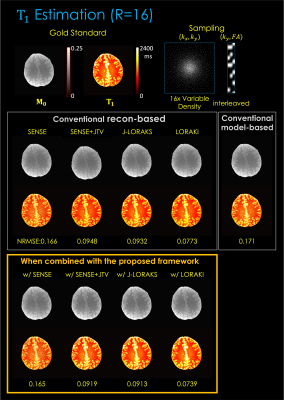
Fig 5. illustrates T1 estimation using 2D R=16x variable density undersampling. The results are consistent, with up to 2.2- and 2.3-fold gain, respectively.
Discussion and Conclusion
We introduced a novel framework for improved MR parameter mapping that can jointly optimize reconstruction- and model-based methods, taking advantage of both. The proposed framework is flexible enough to accommodate different physics models, reconstruction methods and various MR signal relaxation types (T1, T2, T2*, etc). The training was conducted automatically through deep learning toolboxes without having to explore complicated optimization algorithms (when the signal model is differentiable), where it also conveniently admits additional regularization. Accordingly, we could incorporate the scan-specific unsupervised network LORAKI with the model-based parameter mapping, demonstrating improved performance without requiring external training data.Acknowledgements
This work was supported by research grants NIH R01 EB028797, U01 EB025162, P41 EB030006, U01 EB026996, R03 EB031175 and the NVidia Corporation for computing support.References
1. Wang L, Schweitzer ME, Padua A, Regatte RR. Rapid 3D-T1 mapping of cartilage with variable flip angle and parallel imaging at 3.0T. J. Magn. Reson. Imaging 2008;27:154–161 doi: 10.1002/jmri.21109.
2. Doneva M, Börnert P, Eggers H, Stehning C, Sénégas J, Mertins A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magn. Reson. Med. 2010;64:1114–1120 doi: 10.1002/mrm.22483.
3. Huang C, Graff CG, Clarkson EW, Bilgin A, Altbach MI. T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing. Magn. Reson. Med. 2012;67:1355–1366 doi: 10.1002/mrm.23128.
4. Velikina JV, Alexander AL, Samsonov A. Accelerating MR parameter mapping using sparsity-promoting regularization in parametric dimension. Magn. Reson. Med. 2013;70:1263–1273 doi: 10.1002/mrm.24577.
5. Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn. Reson. Med. 2015;73:655–661 doi: 10.1002/mrm.25161.
6. Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang Z-P. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn. Reson. Med. 2015;74:489–498 doi: 10.1002/mrm.25421.
7. Sumpf TJ, Uecker M, Boretius S, Frahm J. Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI. J. Magn. Reson. Imaging 2011;34:420–428 doi: 10.1002/jmri.22634.
8. Sumpf TJ, Petrovic A, Uecker M, Knoll F, Frahm J. Fast T2 Mapping With Improved Accuracy Using Undersampled Spin-Echo MRI and Model-Based Reconstructions With a Generating Function. IEEE Trans. Med. Imaging 2014;33:2213–2222 doi: 10.1109/TMI.2014.2333370.
9. Zhao B, Lam F, Liang Z-P. Model-Based MR Parameter Mapping With Sparsity Constraints: Parameter Estimation and Performance Bounds. IEEE Trans. Med. Imaging 2014;33:1832–1844 doi: 10.1109/TMI.2014.2322815.
10. Roeloffs V, Wang X, Sumpf TJ, Untenberger M, Voit D, Frahm J. Model-based reconstruction for T1 mapping using single-shot inversion-recovery radial FLASH. Int. J. Imaging Syst. Technol. 2016;26:254–263 doi: 10.1002/ima.22196.
11. Wang X, Roeloffs V, Klosowski J, et al. Model-based T1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH. Magn. Reson. Med. 2018;79:730–740 doi: 10.1002/mrm.26726.
12. Hilbert T, Sumpf TJ, Weiland E, et al. Accelerated T2 mapping combining parallel MRI and model-based reconstruction: GRAPPATINI. J. Magn. Reson. Imaging 2018;48:359–368 doi: 10.1002/jmri.25972.
13. Maier O, Schoormans J, Schloegl M, et al. Rapid T1 quantification from high resolution 3D data with model-based reconstruction. Magn. Reson. Med. 2019;81:2072–2089 doi: 10.1002/mrm.27502.
14. Cohen O, Zhu B, Rosen MS. MR fingerprinting Deep RecOnstruction NEtwork (DRONE). Magn. Reson. Med. 2018;80:885–894 doi: 10.1002/mrm.27198.
15. Liu F, Feng L, Kijowski R. MANTIS: Model-Augmented Neural neTwork with Incoherent k-space Sampling for efficient MR parameter mapping. Magn. Reson. Med. 2019;82:174–188 doi: 10.1002/mrm.27707.
16. Liu F, Kijowski R, El Fakhri G, Feng L. Magnetic resonance parameter mapping using model-guided self-supervised deep learning. Magn. Reson. Med. 2021;85:3211–3226 doi: 10.1002/mrm.28659.
17. Jun Y, Shin H, Eo T, Kim T, Hwang D. Deep model-based magnetic resonance parameter mapping network (DOPAMINE) for fast T1 mapping using variable flip angle method. Med. Image Anal. 2021;70:102017 doi: 10.1016/j.media.2021.102017.
18. Kim TH, Garg P, Haldar JP. LORAKI: Autocalibrated Recurrent Neural Networks for Autoregressive MRI Reconstruction in k-Space. ArXiv:1904.09390. 2019.
19. Kim TH, Zhang Z, Cho J, Gagoski B, Haldar J, Bilgic B. Robust Multi-shot EPI with Untrained Artificial Neural Networks: Unsupervised Scan-specific Deep Learning for Blip Up-Down Acquisition (BUDA). In: International Society for Magnetic Resonance in Medicine Annual Meeting (ISMRM). ; 2021. p. 224.
20. Bilgic B, Kim TH, Liao C, et al. Improving parallel imaging by jointly reconstructing multi-contrast data. Magn. Reson. Med. 2018;80:619–632 doi: 10.1002/mrm.27076.
21. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn. Reson. Med. 1999;42:952–962 doi: 10.1002/(SICI)1522-2594(199911)42:5<952::AID-MRM16>3.0.CO;2-S.
22. Chen C, Li Y, Huang J. Calibrationless Parallel MRI with Joint Total Variation Regularization. In: Medical Image Computing and Computer-Assisted Intervention – MICCAI 2013. Berlin, Heidelberg: Springer; 2013. pp. 106–114. doi: 10.1007/978-3-642-40760-4_14.
23. Kim TH, Setsompop K, Haldar JP. LORAKS makes better SENSE: Phase-constrained partial fourier SENSE reconstruction without phase calibration. Magn. Reson. Med. 2017;77:1021–1035 doi: 10.1002/mrm.26182.
Figures
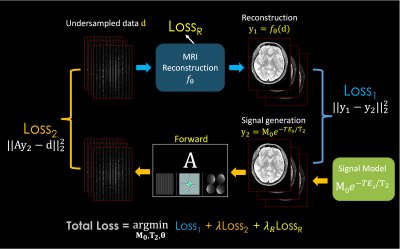
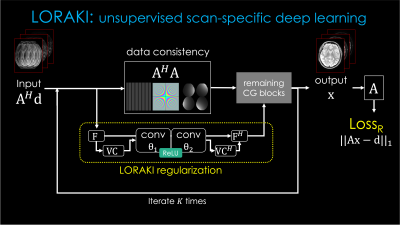
Fig. 2. LORAKI reconstruction pipeline for multi-echo MRI reconstruction, based on an unrolled conjugate gradient (CG) of the SENSE-LORAKS reconstruction. A: the forward model as in Fig. 1, d: the undersampled multi-echo data, F: Fourier transform, VC: Virtual conjugate coils, H: Hermitian adjoint, conv: convolution layers parameterized by θ = [θ1T, θ2T]T which are subject to be trained.
This LORAKI reconstruction was integrated into the “MRI Reconstruction” block in Fig. 1 and the parameters (e.g. M0, T2, θ) were optimized jointly using the total loss with the Adam optimizer.
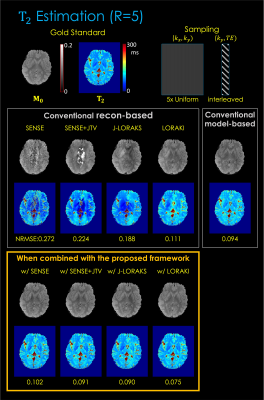
Fig. 3. T2 estimation results. The top row displays the gold standard M0 and T2 parameter maps estimated from fully sampled (R=1) data using the least-squares fitting. The middle row displays the conventional reconstruction-based and model-based MR parameter mapping approaches. The button row displays the proposed method combined with each reconstruction technique. The NRMSE was taken between the fully sampled data and the synthetic data generated from the estimated parameter maps.