4400
A Review and Comparison of Unwrapping Methods in Dual Velocity-Encoding MRI1Biomedical Imaging Center, School of Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile, 2Millennium Nucleus for Cardiovascular Magnetic Resonance, Santiago, Chile, 3Electrical Engineering Department, School of Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile, 4Department of Biomedical Engineering, McCormick School of Engineering, Northwestern University, Chicago, IL, United States, 5Department of Radiology, Feinberg School of Medicine, Northwestern University, Chicago, IL, United States, 6Institut für Physik, Universität Greifswald, Greifswald, Germany, 7Bernoulli Institute, University of Groningen, Groningen, Netherlands, 8Radiology Department, School of Medicine, Pontificia Universidad Católica de Chile, Santiago, Chile
Synopsis
4D flow MRI data may be inaccurate due to phase wrapping when using lower VENC than the maximum actual velocity. Accuracy can also be affected by reduced velocity-to-noise ratio (VNR) when using a too high VENC. Dual-VENC approaches have been proposed to unwrap velocity-aliasing artifacts and increase VNR, providing more reliable measurements and allowing more flexibility in the selection of VENC. Dual-VENC methods enable acquisitions of 4D flow MRI data with high dynamic range and without velocity aliasing. The purpose of this study is to compare the performance of some of these methods.
Introduction
4D flow MRI enables velocity quantification by subtracting two measured phases of the complex transverse magnetization in MRI1-5. However, it is inherently limited by the need to set a velocity-encoding sensitivity (VENC). VENC is inversely proportional to the Velocity-to-Noise-Ratio in the final measured velocity map. Therefore, setting up the VENC is important to obtain velocity data with high VNR without wrapping artifacts6. Moreover, even for VENC values slightly larger than the true velocity, velocity aliasing may occur due to measurement noise7-9. Furthermore, for some applications, it is essential to obtain quantitative information of low and high blood flow velocities simultaneously, which can differ by orders of magnitude, even in normal subjects. Images obtained with low VENC and the use of an unwrapping method can be applied. However, this approach sometimes fails to properly unwrap all aliased voxels. To solve this issue, dual-VENC approaches have been proposed10. Schnell et al. previously developed a dual-VENC 4D flow MRI sequence using a shared reference scan followed by two successive interleaved, as shown in Figure 1a, which allowed for the encoding of 3D blood flow velocities with 7-point encoding11. Other dual-VENC methods include the Standard Dual-VENC (SDV)11-13, Optimal Dual-VENC (ODV)14, and triple-VENC (TV)15 (Figure 1b). Nevertheless, noise, processing errors, undersampling, and spurious artifacts make the unwrapping of the data sometimes difficult. This work aims to perform a one-to-one comparison of the unwrapping methods (SDV, ODV, and TV) using in-vitro and in-vivo datasets, including an assessment of noise in the final results.Methods
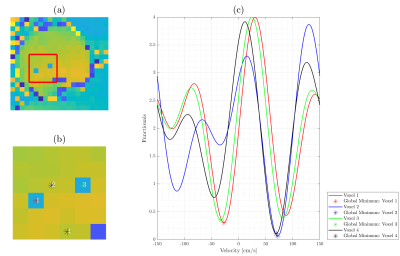
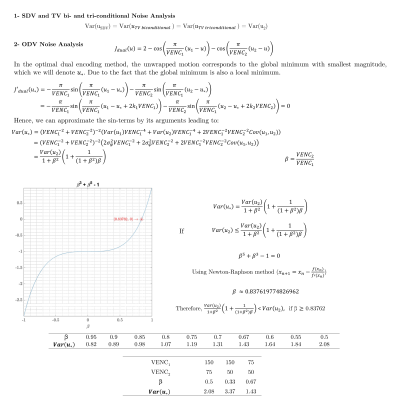
Multi-VENC 4D flow MRI data were acquired in a constant rotation and pulsatile flow phantoms using a 1.5T MAGNETOM Aera System (Siemens Healthineers, Erlangen, Germany). Additionally, 2D PC-MRI data were acquired in eight healthy volunteers using a clinical 1.5T MR Scanner (Philips). The raw data was obtained, and the reconstruction of each bipolar gradient was performed offline using MATLAB16. Data from the multiple coils were combined using the proposed method17. We used VENCs of 50, 75, and 150 cm/s for the in-vitro and in-vivo datasets. We implemented and compared the SDV, ODV, and TV methods. Furthermore, we developed a new correction method for ODV. For ODV, the presence of noise deforms the dual-VENC function, as in Figure 2(c). The global minima with the smallest absolute value may be incorrect, and velocity aliasing occurs, such as it happens in points 1 and 3. Nevertheless, due to the ODV formulation, we can correct it using the cost function values as explained next. For every pixel of the image, we found 8-connected pixels, calculating the mean velocity of the neighborhood. If the mean value has the same sign as a central pixel. Then, we found a local minimum (positive or negative, according to the case). And finally, replace the velocity value in the pixel image. Finally, we also present an analytical noise analysis of the velocity estimates of the different methods.Results
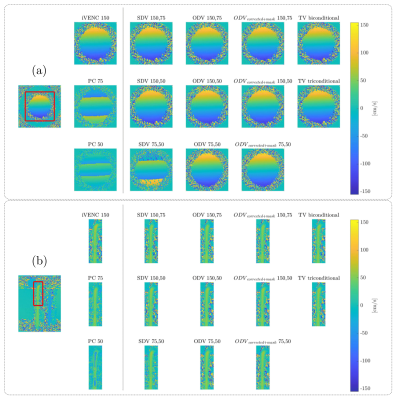
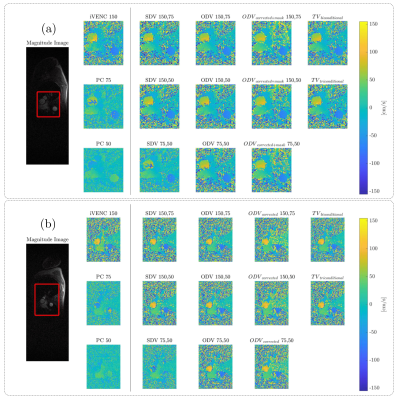
The unwrapping results for the constant rotation and pulsatile flow phantoms are presented in Figure 3. The ODV and TV algorithms successfully unwrapped all voxels without any residual velocity aliasing. Figures 4 shows the velocity profiles on the ascending and descending aorta in two volunteers, using the same VENC combinations and reconstruction methods. The SDV cannot handle the aliasing when both VENC values are lower than the true velocity (i.e., 75,50). In contrast, ODV and TV can successfully reconstruct unaliased images from two aliased ones. Nevertheless, TV triconditional outperformed TV biconditional method. Furthermore, the ODV corrected unwrapping algorithm successfully unwrapped all voxels without any residual velocity aliasing. Regarding the computational time, ODV was slower than TV and SDV (ODV: ≈ 96.0 s, TV-biconditional: ≈ 1.8 s, TV-triconditional: ≈ 3.6 s, and SDV: ≈ 0.4 s). For noise analysis, we analytically computed the velocity estimate variance (Var(u)), as shown in Figure 5. The SDV and TV methods led to Var(uSDV) = Var(uTV) = Var(u2) when the unwrapping was successful. Nonetheless, in the classical ODV method – when both VENC images share the background phase – only if β ≥ 0.8376, then Var(u*) ≤ Var(u2).Conclusions
The ODV and TV unwrapping methods outperformed SDV and led to comparable results in both phantom and volunteers. While the ODV technique required longer computational times, it demonstrated the potential of correcting wrong unwrapping results at isolated voxels thanks to its mathematical formulation.Acknowledgements
This publication was funded by ANID – Millennium Science Initiative Program – NCN17_129. Also, has been supported by CONICYT - PIA - Anillo ACT1416, CONICYT FONDEF Concurso I+D ID18I10064, FONDECYT #1181057. Franco P. thanks to ANID – PCHA/ Doctorado-Nacional/2018-21180391, and National Institutes of Health (1F30HL137279, NIH 1R01HL149787).References
1.- Wu SP, Ringgaard S, Pedersen EM, Three-dimensional phase contrast velocity mapping acquisition improves wall shear stress estimation in vivo. Magn Reson Imaging. 2004; 22(3):345-351.
2.- Wigstrom L, Ebbers T, Fyrenius A, Karlsson M, Engvall J, Wranne B, Bolger AF. Particle trace visualization of intracardiac flow using time-resolved 3D phase contrast MRI. Magn Reson Med. 199; 41(4):793-799.
3.- Markl M, Harloff A, Bley TA, Zaitev M, Jung B, Weigang E, Langer M, Hennig J, Frydrychowicz A. Time-resolved 3D MR velocity mapping at 3T: improved navigator-gated assessment of vascular anatomy and blood flow. J Magn Reson Imaging. 2007; 25(4):824-831.
4.- Kvitting JP, Ebbers T, Wigstrom L, Engvall J, Olin CL, Bolger AF. Flow patterns in the aortic root and the aorta studied with time-resolved, 3-dimensional, phase-contrast magnetic resonance imaging: implications for aortic valve-sparing surgery. J Thorac Cardiovasc Surg. 2004; 127(6): 1602-1607.
5.- Stalder AF, Russe MF, Frydrychowicz A, Bock J, Henning J, Markl M. Quantitative 2D and 3Dphase contrast MRI: Optimized analysis of blood flow and vessel wall parameters. Magn Reson Med. 2008; 60(5):1218-1231.
6.- Markl M, Frydrychowicz A, Kozerke S, Hope M, Wieben O. 4D flow MRI, J Margn Reson Imaging. 2012; 36(5):1015-36.
7.- Ha H, Kim GB, Kweon J, Lee SJ, Kim YH, Lee DH, Yang DH, Kim N. Hemodynamic Measurement Using Four-Dimensional Phase-Contrast MRI: Quantification of Hemodynamic Parameters and Clinical Applications, Korean J Radiol. 2016; 17(4): 445.62.
8.- Pelc NJ, Bernstein MA, Shimakawa A, Glover GH, Encoding strategies for three-direction phase-contrast MR imaging of flow, Journal of Magnetic Resonance Imaging. J Magn Reson Imaging. 1991;1(4), 405-413
9.- Yang GZ, Burger P, Kilner PJ, Karatowski SP, Firmin DN. Dynamic range extension of cine velocity measurements using motion-registered spatiotemporal phase unwrapping. J Magn Reson Imaging. 1996; 6(3): 495-502.
10.- Johnson M and Markl M, Improved SNR in Phase Contrast Velocimetry with 5-Point Balanced Flow Encoding. Magn Reson Med. 2010; 63(2): 349-355.
11.- Schnell S, Ansari SA, Wu C, Garcia J, Murphy IG, Rahman OZ, Rshsepar AA, Aristova M, Collins JD, Carr JC, and Markl M, Accelerated Dual-VENC 4D flow MRI for neurovascular applications, J Magn Reson Imaging. 2017; 46(1): 102-114.
12. - Ghiglia D and M. Pritt D, Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software (Wiley, 1998).
13.- Lee AT, Pike B and Pelc NJ, Three-Point Phase-Contrast Velocity Measurements with Increased Velocity-to-Noise Ratio,Magn Reson Med. 1995; 33(1):122-6.
14.- Carrillo H, Osses A, Uribe S and Bertoglio C. Optimal Dual-VENC (ODV) Unwrapping in Phase-Contrast MRI. IEE Trans Med Imaging. 2019; 38(5):1263-1270.
15. – Ma LE, Markl M, Chow K, Vali A, Wu C, Schnell S. Efficient triple-VENC phase-contrast MRI for improved velocity dynamic range. Magn Reson Med.
16.- Lorenz R, Benk C, Bock J, et al. Closed circuit MR compatible pulsative pump system using a ventricular assist device and pressure control unit. Magn Reson Med. 2012; 67:258-268.
17.- Bernstein MA, Grgic Mladen, Brosnan TJ, Pelc NJ. Reconstructions of Phase Contrast, Phased Array Multicoil Data. Magn Reson Med. 1994; 32(3):330-4.
Figures