Introduction

In fetal brain MRI, the fetal motions are commonly seen within the 2D multi-slice stacks_¹. The conventional volume reconstruction method for T1/T2-weighted fetal brain MRI consists of motion correction based on slice-to-volume registration (SVR) and super-resolution reconstruction (SRR). In these processes, a reference stack with minimal motion needs to be determined as the template for initial volume-to-volume registration, and also as the template for SVR after being interpolated into isotropic volume^2-4. Previously, the reference stack was determined manually or through a flattening-based method with lower sensitivity to motion. In this paper, we proposed two methods to quantitatively assess motion across slices within stack based on singular value decomposition (SVD) and CANDECOMP/PARAFAC decomposition (CP), and tested their performance on both simulated and real-world fetal brain motions.

Methods

Data acquisition: A total of 110 fetal brain MRI (gestational age: 21-40 weeks) with three orthogonal orientations (axial/coronal/sagittal) were collected on a 3T Siemens Skyra scanner with an abdominal coil using T2-weighted half-Fourier single-shot turbo spin-echo (HASTE) with the following protocol: TR/TE=800/97ms, in-plane resolution=1.09×1.09mm, FOV=256×200mm, thickness=2mm, GRAPPA factor=2.
Data preprocessing and motion simulation: We first used the NiftyMIC toolkit⁵ to reconstruct 3D volume at 0.8*0.8*0.8 resolution, through bias field correction, motion correction and SRR, which was used as ground truth. The motion was randomly simulated by six degree of freedom (6-dof) with translation and rotation between the slices to obtain motion-corrupted stacks (Fig. 2).
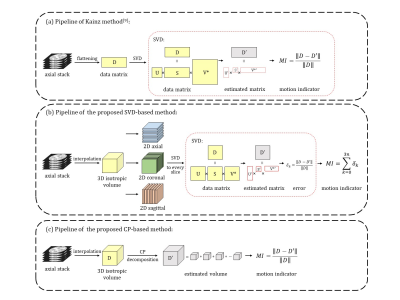
SVD-based method: MRI 2D data matrix (D) can be divided into a low-rank component and a sparse component that corresponds to high-frequency noise caused by motion and structural difference^6,7. The 2D matrix can be decomposed using SVD, and the first r singular values and singular vectors can be selected to obtain the estimation matrix (D’) as the low-rank component of D with rank r⁸. Fetal motion results misaligned slices and an increase in the number of linearly independent slices. Therefore, the sparse components, so-called error, will increase with motion if the matrix rank is fixed. The error between origin data and low-rank estimated data can be used as a motion indicator (MI). In this work, we used the ratio of motion-corrupted indicator to motion-free indicator, namely, the relative MI (RMI), to access motion.
Previous method flattened slices into vectors as rows of data matrix (Figure 1a) to assess motion as SVD is only applied to 2D matrix⁹, which lose the spatial information, and the stack in different orientations cannot be guaranteed to have similar baseline MI because of the inherent structural difference. Considering the inter-slice motion mainly result in slice misalignment and the image features along the non-principle axes provide important motion information, we performed SVD on re-sliced 2D images along all three axes and calculated the sum of errors to represent the fetal motion. To ensure all stacks have similar baseline MI, we interpolate each stack into isotropic volume before re-slicing. (Figure 1b).
CP-based method: CP decomposition is a tensor decomposition method that allows principal component analysis of 3D volumes¹⁰. It transforms a tensor into a sum of rank-one tensor, which can be expressed as the outer product of three vectors. For a given small rank r, the difference between the original tensor and r rank-one tensors gives the sparse component containing motion information for MI calculation (Figure 1c).

Results

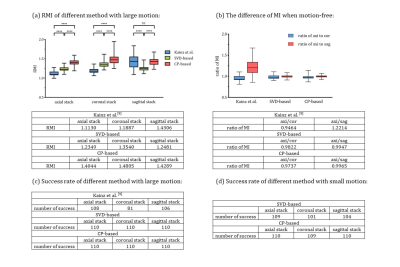
Simulation experiments: We simulated two groups of motions, with 5° rotation/1mm translation (large motion) and 2° rotation/0.4mm translation (small motion) between adjacent slices (Figure 2). The SVD-based and CP-based methods proposed here showed higher RMI than Kainz method, indicating higher sensitivities using our methods. Moreover, the proposed method had less bias and baseline error between different stacks (Figure 3b), which is important for determining the minimal-motion stack.
We then tested the successful detection rate by distinguishing one motion-free stack from two motion-corrupted stacks. The success rate of SVD-based and CP-based method was 100%, better than Kainz method of 89.4%. In the small motion group, the success rate of SVD-based and CP-based method were 95.2% and 99.7%, respectively (Figure 3c, 3d).
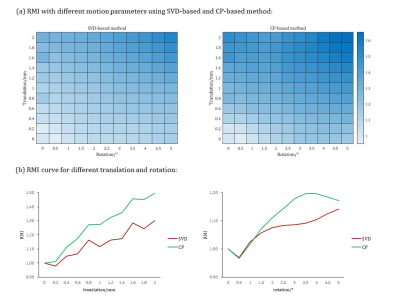
We also simulated various motion parameters (T∈[0,2]mm, R∈[0,5]°) to test the performance under different motions. The result showed RMI became larger with the increase of motion amplitude, and CP-based method had maximum sensitivity to motion among the three methods (Figure 4).
Real-world fetal MRI experiments: We combined the CP-based motion assessment algorithm with the NiftyMIC pipeline as a prior step to automatically determined the reference stack, and compared the final reconstruction results with the default pipeline that always take the first input stack (axial stack) as a reference. The volume reconstructed with motion assessment provides better quality with the lower normalized root mean square error (NRMSE) of 0.149 and higher structural similarity (SSIM) of 0.985 than using the default pipeline (Figure 5).

Discussion and conclusion

The proposed SVD-based method and CP-based method showed better performance in motion assessment than previous work, as they were more sensitive to motion and provide higher success rate in detecting minimal-motion slice and more consistent baseline MI among different stacks. The motion assessment method can be used to automatically select the minimal motion stack as a reference for the SVR-SRR fetal brain reconstruction pipeline, which improved the reconstruction stability.