4386

Ultrafast B₁ Mapping with RF-Prepared 3D FLASH Acquisition: Correcting the Bias due to T₁-Induced k-Space Filtering Effect

Dan Zhu^1,2 and Qin Qin^1,2
¹F.M. Kirby Research Center for Functional Brain Imaging, Kennedy Krieger Institute, Baltimore, MD, United States, ²The Russell H. Morgan Department of Radiology and Radiological Science, Johns Hopkins University School of Medicine, Baltimore, MD, United States

Synopsis

The traditional RF-prepared B₁ mapping technique consists of one scan with an RF preparation module for FA-encoding and a second scan without this module for normalizing. To reduce the T₁-induced k-space filtering effect, this method is limited to 2D FLASH acquisition with a two-parameter method. Based on the point spread function analysis of FLASH readout, a novel 3D RF-prepared three-parameter method for B₁-mapping is proposed to correct the T₁-induced quantification bias. The proposed technique was compared with existing methods in the brain, breast, and abdomen and demonstrated with high accuracy for ultrafast B₁ mapping.

Introduction

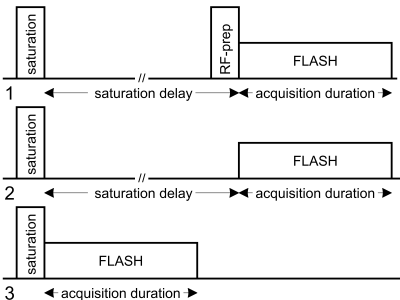
Rapid measurement of the spatial variation of the flip angles (FA) for the organs of interest is desired for many MRI applications. The RF-prepared two-parameter method^1,2 starts with a B₁-insensitive saturation module and a fixed saturation delay, then applies an RF preparation module for B₁-encoding in the first scan and removes this module for normalizing in the second scan, both followed with FLASH acquisition. To reduce the T₁-induced k-space filtering effect, this method is limited to a short 2D readout. In this work, a novel 3D RF-prepared method for ultrafast B₁-mapping is proposed with a third scan to record and correct the bias from the k-space filtering effect (three-parameter method). We compared the 3D RF-prepared method with existing B₁ mapping methods in the brain, abdomen and breast with different RF-shim settings at 3T.

Theory

The proposed protocol is illustrated in Figure 1. The ratio between the longitudinal magnetization after an RF-prep pulse ($$$M_{FA}$$$) with FA=$$$\alpha$$$ and the normalizing magnetization without this RF-prep pulse ($$$M_{norm}$$$) is:$$\frac{M_{FA}}{M_{norm}}=\frac{M_{norm}\cdot\cos{(\alpha)}}{M_{norm}}=\cos{(\alpha)}.\tag{1}$$
The point spread function analysis of FLASH shows that the prepared longitudinal magnetization before the FLASH acquisition ($$$M_{FA}$$$, or $$$M_{norm}$$$) and the image signal ($$$S_{FA}$$$, or $$$S_{norm}$$$) obeys a linear (not proportional) relationship (slope=$$$a$$$, intercept=$$$b$$$). $$S_{norm}=a\cdot M_{norm}+b\tag{2}$$$$S_{FA}=a\cdot M_{FA}+b\tag{3}$$
In this work, we propose to obtain the intercept b via a third image, by acquiring the signal immediately after the saturation module: $$S_{sat}=a\cdot 0+b=b.\tag{4}$$
Using a three-parameter method, the bias in FA estimation can thus be corrected:$$\frac{S_{FA}-S_{sat}}{S_{norm}-S_{sat}}=\frac{a\cdot M_{norm}\cdot\cos{(\alpha)}+b-b}{a\cdot M_{FA}+b}=\cos{(\alpha)}.\tag{5}$$
The relationship of the actual FA ($$$\alpha$$$) and the nominal FA ($$$\alpha^{nom}$$$) is usually described with a scale factor $$$\kappa$$$ (with 100% as consistent between the two): $$\kappa=\frac{\alpha}{\alpha^{nom}}\times100\%=\frac{\cos^{-1}{\left(\frac{S_{FA}-S_{sat}}{S_{norm}-S_{sat}}\right)}}{\alpha^{nom}}\times100\%.\tag{6}$$
It is important to note that subtractions between $$$S_{FA}$$$, $$$S_{norm}$$$ and $$$S_{sat}$$$ should consider opposite polarities and complex subtraction is preferred in this case.

Methods

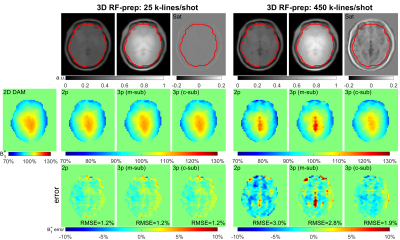
In vivo datasets of three brains, three breasts and five abdomens were obtained from six volunteers (4 females, 25-45yrs), performed on a 3T Philips Ingenia scanner with a dual-source parallel RF excitation system. A 32-channel head coil, a 16-channel bilateral breast coil and a 32-channel chest coil were used for signal reception, respectively.

For the three-parameter method, the RF-prep utilized $$$\alpha^{nom}$$$=60°. The FLASH acquisition had a low-high ordering. For brain scans: TR/TE=3.4/2.3ms, FOV=220×220×120mm³, resolution=4×4×4mm³, readout bandwidth(BW)=2975Hz/pixel. The number of k-lines per shot were varied: 25,50,100,225,450. Corresponding FA=18°,13°,9°,6°,5° for optimal signal contrast. Different saturation delays=0.75,2.0,5.0,10.0,20.0s. For breast and abdomen scans, FOV=350×350×180mm³, resolution=6×6×6mm³, BW=2854Hz/pixel. Compressed-sensing factor=3 in all scans. Abdomen scans were acquired during one breath-hold.

Five other B₁ mapping methods for comparison: 1) Single-slice double-angle method (DAM) with 60°/120° excitation FA with TR=20s; 2) Single-slice Saturated DAM (SDAM)^3,4 with a saturation delay of 0.5s and TR=0.58s; 3) Multi-slice SDAM with 30 slices; 4) Multi-slice DREAM^5-8 with 30 slices, TR/TE_STE/ TE_FID=4.5/1.7/2.3ms, STEAM/FLASH FA=60°/15°, TR extension=8.5s; 5) 3D AFI⁹ with TR₁/TR₂/TE=20/100/4.6ms, FA=60°.

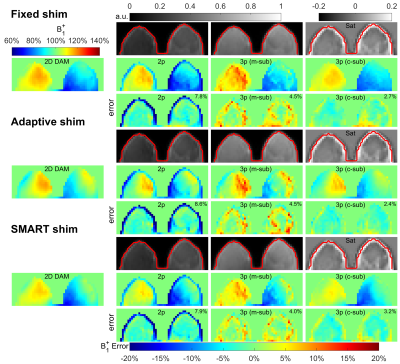
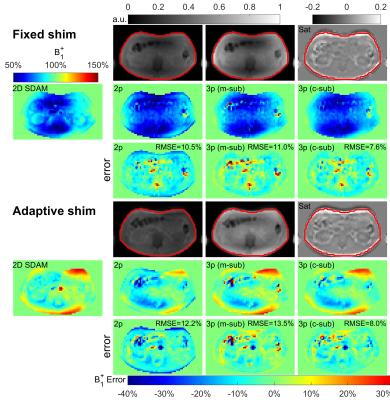
Standard single-source B₁ shimming (“Fixed”) was used for all three organs. For breast and abdomen scans, a dual-source B₁ shimming (“Adaptive”) was also performed. A vendor-provided B₁ shimming method based on geometries of individual breasts (“SMART”) was also applied for breast scans.

B₁⁺ maps of the proposed method were calculated with Eq. (6) with both magnitude and complex subtractions. A mask for each B₁ map was manually drawn from respective raw images. Within the mask area, the B₁ maps were quantitatively compared with the DAM (SDAM for abdomen scans) using four metrics: 1) root mean square error (RMSE), 2) error mean, 3) error standard deviation (SD), 4) concordance correlation coefficients (CCC).

Results

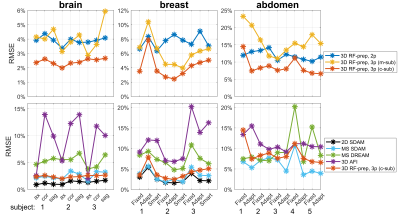
Figures 2,3,4 shows the results of an axial slice of a subject’s brain, breast, and abdomen with the calculated B₁⁺ scale maps from the 2D DAM method, the 3D RF-prepared two-parameter method and the proposed three-parameter method using both magnitude- and complex-subtractions, and their respective difference maps, under different shim settings respectively.

When combining comparison results from all three organs of all the subjects, including three orientations for each of the three brains, three shimming conditions for each of three breasts, two shimming conditions for each of the five abdomens, the RMSE, error mean, error SD, and CCC values of each B₁ mapping method comparing to 2D DAM or SDAM methods for each organ are plotted in Figure 5.

Compared to the 3D RF-prepared two-parameter method, the three-parameter method using complex-subtraction yielded the averaged RMSE 38% lower in the brain (2.4% vs. 3.9%), 45% lower in the breast (4.2% vs. 7.7%), and 27% lower in the abdomen (8.7% vs. 11.9%); its CCC values were 5.9% higher in the brain (95.9% vs. 90.6%), 22% higher in the breast (83.0% vs. 68.1%), and 28% higher in the abdomen (68.2% vs. 53.1%). Based on these quantitative metrics, the 3D RF-prepared three-parameter method with complex-subtraction delivered consistently lower RMSE, error mean, error SD, and higher CCC values than multi-slice DREAM and 3D AFI, and were close to the results of 2D or multi-slice SDAM (Figure 5).

Conclusion

The proposed 3D RF-prepared three-parameter method with complex-subtraction was demonstrated with high accuracy for B₁ mapping in brain, breast, and abdomen, while only taking a fraction of time of existing methods.

Acknowledgements

No acknowledgement found.

References

1. Chung S, Kim D, Breton E, Axel L. Rapid B1+ Mapping Using a Preconditioning RF Pulse with TurboFLASH Readout. Magn Reson Med. 2010;64(2):439-446.

2. Breton E, McGorty K, Wiggins GC, Axel L, Kim D. Image-guided radio-frequency gain calibration for high-field MRI. NMR Biomed. 2010;23(4):368-374.

3. Cunningham CH, Pauly JM, Nayak KS. Saturated double-angle method for rapid B1+ mapping. Magn Reson Med. 2006;55(6):1326-1333.

4. Sung K, Nayak KS. Measurement and characterization of RF nonuniformity over the heart at 3T using body coil transmission. Journal of Magnetic Resonance Imaging. 2008;27(3):643-648.

5. Nehrke K, Bornert P. DREAM-a novel approach for robust, ultrafast, multi-slice B1 mapping. Magn Reson Med. 2012;68(5):1517-1526.

6. Nehrke K, Versluis MJ, Webb A, Bornert P. Volumetric B1+ mapping of the brain at 7T using DREAM. Magn Reson Med. 2014;71(1):246-256.

7. Hooijmans MT, Dzyubachyk O, Nehrke K, et al. Fast multistation water/fat imaging at 3T using DREAM-based RF shimming. J Magn Reson Imaging. 2015;42(1):217-223.

8. Nehrke K, Sprinkart AM, Bornert P. An in vivo comparison of the DREAM sequence with current RF shim technology. MAGMA. 2015;28(2):185-194.

9. Yarnykh VL. Actual flip-angle imaging in the pulsed steady state: a method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn Reson Med. 2007;57(1):192-200.

Figures

Figure 1: Pulse sequence of the 3D RF-prepared B₁ mapping technique for the proposed three-parameter method. The 3D FLASH acquisition with low-high profile ordering is applied. In the first scan, an RF-prep module with a short hard pulse (FA=α) is followed by FLASH readout to generate an FA-encoded image; In the second scan, a normalizing image without applying the RF-prep module is acquired; In the third scan, the FLASH acquisition is applied immediately after the B₁-insensitive saturation module in order to obtain the imaging bias induced by the T₁ relaxation during the long readout.

Figure 2: Evaluating the 3D RF-prepared B₁ mapping in the brain. (top): the FA-encoded (FA), the normalizing (norm), and the saturated (sat) images acquired with 25 and 450 k-lines per shot for 3D FLASH acquisition and a saturation delay of 3.0s, with the tissue masks labeled in solid red lines; (middle): the B₁⁺ maps using the 2D DAM, the RF-prepared two-parameter method (2p), and the three-parameter method (3p) with both magnitude-subtraction (m-sub) and complex-subtraction (c-sub); (bottom): their corresponding error maps with root mean square error (RMSE) labeled at the bottom.

Figure 3: Evaluating the 3D RF-prepared B₁ mapping in the breast under fixed, adaptive, and SMART shims, respectively. For each shim condition, (top): the FA-encoded (FA), the normalizing (norm), and the saturated (sat) images, with the tissue masks labeled in solid red lines; (middle): the B₁⁺ maps using the 2D DAM, the 3D RF-prepared two-parameter method (2p), and the three-parameter method (3p) with both magnitude-subtraction (m-sub) and complex-subtraction (c-sub); (bottom): corresponding error maps with root mean square error (RMSE) indicated at the top right corners.

Figure 4: Evaluating the 3D RF-prepared B₁ mapping in the abdomen under fixed and adaptive shims, respectively. For each shim condition, (top): the FA-encoded(FA), the normalizing (norm), and the saturated (sat) images, with the tissue masks labeled in solid red lines; (middle): the B₁⁺ maps using the 2D DAM, the 3D RF-prepared two-parameter method (2p), and the three-parameter method (3p) with both magnitude-subtraction (m-sub) and complex-subtraction (c-sub); (bottom): corresponding error maps with averaged root mean square error (RMSE) indicated at the top right corners.

Figure 5: The root mean square error (RMSE) values of each method compared to 2D DAM or SDAM with three orientations for each of the three brains, three shimming conditions for each of three breasts, two shimming conditions for each of the five abdomens. Total scan times (brain/breast/abdomen) are 40/40/NA s for 2D DAM, 1/1/1s for 2D SDAM, 35/35/17s for MS SDAM (Abdomen FH resolution=12mm), 17/17/17s for MS DREAM, 148/148/15s for 3D AFI (Abdomen FH FOV=18mm), 7/7/7s for 2p RF-prep, and 8.6/8.6/8.6s for 3p RF-prep. FOV and resolutions not specified are identical to the RF-prep scans.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

4386

DOI: https://doi.org/10.58530/2022/4386