Introduction

There is an increasing interest in ultra-low-field (ULF) MRI for low-cost, low-power and point-of-care clinical applications [1-4]. The Halbach magnet array features low-cost, lightweight and easy-to-maintain advantages, making it an ideal choice for portable ULF magnets [1-3]. However, all rare earth magnet materials are sensitive to temperature. Temperature-induced B0 drifting and inhomogeneity can easily arise during scanning due to environments or gradient coil heating.

One may use more temperature-insensitive materials for Halbach array construction [5-7]. However, such rare earth materials are difficult to access and expensive. Here we present a temperature-insensitive Halbach array design, which can provide a stable B0 field in presence of global or local temperature changes.

Theory and Method

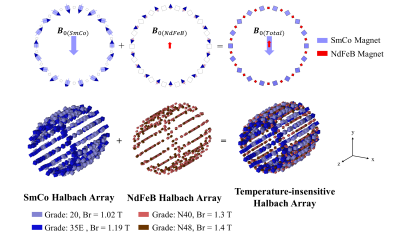
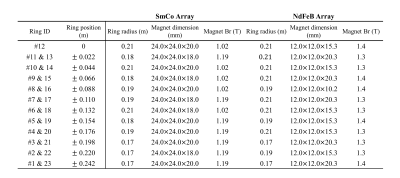
The field strength of magnets generally behaves as a linear function of temperature, as determined by a negative reversible temperature coefficient α (unit: ppm/ºC). The temperature compensation approach [4] is adopted here. This design interleaves two Halbach arrays that are constructed by two rare earth magnet materials of very different temperature coefficients and with opposite magnetization directions. This is to cancel out the temperature-induced changes in B0 at a minor cost to magnet efficiency. In this study, SmCo magnets (primary array) and NdFeB magnets (compensation array) are chosen for their large difference in temperature coefficient ( α_SmCo is -300 ppm/ºC and α_NdFeB is -1400 ppm/ºC). Consequently, the two arrays’ ratio of B0 is determined based on their material’s temperature coefficient, satisfying that B0_SmCo/B0_NdFeB=α_NdFeB/α_SmCo.

The proposed cylindrical array consists of 23 rings. In each ring, 18 SmCo magnets and 18 NdFeB magnets are alternately arranged (FIGURE 1). To improve homogeneity, genetic algorithm (GA) is applied here to find optimal choices of magnet grades, sizes of individual magnet elements, and their ring radii. SmCo and NdFeB arrays are optimized by GA independently. Halbach array length is chosen to be ~50 cm. The individual element volume is empirically chosen to be 10.4-11.5 cm³ and 2.19-2.92 cm³ and for SmCo and NdFeB elements, respectively. See TABLE1 for other key design parameters.

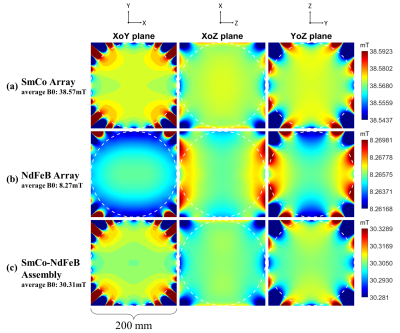
At 26.85°C (300 K), the SmCo array generates a B0 at ~38mT in the -y direction (see FIGURE 2a), and the NdFeB array generates a B0 at ~8mT in the +y direction (see FIGURE 2b). B0 strength of the final assembly is ~30 mT (see FIGURE 2c). The overall inhomogeneity is ~1500 ppm. For comparison, a pure SmCo Halbach is designed by modifying the SmCo array of the temperature-sensitive design. The only difference is that the size of each magnet element is scaled by a factor of 0.8, so this array also generates a B0 field along the -y direction at about 30 mT. Its inhomogeneity is ~1200 ppm. The weight of the proposed design is 49.4 kg (SmCo array 40.8 kg, NdFeB array 8.6 kg). In comparison, the weight of pure SmCo Halbach array is 32 kg.

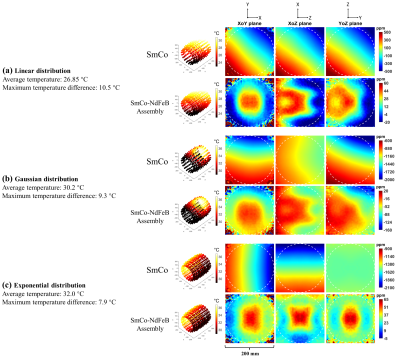
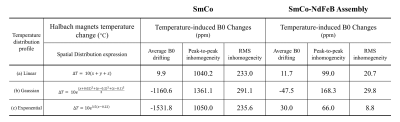
Finite element simulation using CST is conducted to study the design performance with regard to spatially uniform and non-uniform temperature changes. Three types of non-uniform temperature profiles (linear distribution along x, y and z directions; spatially isotropic Gaussian distribution; and exponential distribution along x direction) are simulated. Their temperature distributions or maps are shown in FIGURE 3 (left) and simulation details are given in TABLE 2. B0 changes are acquired by comparing Halbach arrays in presence of these temperature distributions with Halbach arrays at 26.85°C (uniform).

Results

Numerical simulation indicates that the overall B0 drifting due to global uniform temperature changes is generally removed in the proposed design, while small B0 drifting still can be observed when non-uniform temperature changes occur. In cases of three non-uniform temperature change profiles, the drifting of average B0 is suppressed to <50 ppm. The temperature-induced inhomogeneity in the proposed design is ~10% of that in the pure SmCo Halbach array. The B0 changes caused by non-uniform temperature changes are shown in FIGURE 3 (right). They are quantified and summarized in TABLE 2.

Discussion and Conclusions

This temperature-insensitive Halbach array design features significantly improved stability to both spatially uniform and non-uniform temperature changes, yielding a very stable B0 field under various temperature change profiles. With such high immunity to temperature changes, the proposed temperature-insensitive design is made suitable for air-conditioning-free or/and outdoor scenarios. The configuration of the SmCo and NdFeB arrays can be optimized. For example, a more uniform distribution of SmCo and NdFeB magnets may further reduce the intrinsic B0 inhomogeneity (in absence of any temperature changes) and temperature-induced B0 inhomogeneity. In this design, SmCo and NdFeB magnets are chosen for Halbach array construction. Without loss of generality, one can choose other materials to build temperature-insensitive arrays in the same scheme. A further improvement of magnet efficiency is possible when materials with higher temperature coefficient differences are available.

Acknowledgements

This work was supported in part by Hong Kong Research Grant Council (R7003-19F, HKU17112120 and HKU17127121 to E.X.W., and HKU17103819, HKU17104020 and HKU17127021 to A.T.L.L.), Lam Woo Foundation, and Guangdong Key Technologies for Treatment of Brain Disorders (2018B030332001) to E.X.W..