INTRODUCTION

Spectroscopic research plays an important role in both NMR and MRI fields. NMR Spectroscopy is widely used in life sciences, drug treatments, petroleum, and petroleum¹. And in vivo MRS allows noninvasive analysis of metabolites and can provide information on pathogenesis, monitoring metabolite responses, and clinical diagnosis of cancers. MR Spectroscopy is mainly presented in its absorption mode, which has advantages over amplitude mode or power mode in terms of higher resolution and more accurate quantitative information about spin concentration². However, the spectrum after fourier transform is not always absorbed for many reasons, including the misalignment of the reference phase relative to the receiver phase detector, amplifier dead time, and phase shift of digital filters used to reduce noise³. Therefore, phasing the spectrum is one of the necessary procedures for the post-processing of Spectroscopy. Although manual phase correction can obtain a generally satisfying result by carefully tuning the Ph0 and Ph1, it is very time-consuming, especially in the batch processing of NMR spectra. Moreover, in vivo MRS subject motion often leads to changes in the quality of water suppression and excitation of subcutaneous lipid signals, resulting in artifacts⁴.
Many automatic phase correction methods have been published over the years^5,6. The search-based phase correction algorithms are developing towards increasing constraints and finer steps. Still, these algorithms have some defects in some aspects, such as dependence on linearity⁵, sensitivity to signal-to-noise ratio, and baseline distortion⁷. Moreover, these methods often have poor correction effects for spectra with complex peak shapes and baseline changes, such as metabolomics spectra⁴. We fuse traditional methods and neural network to propose a more robust and accurate method based on predicted Ph0 and Ph1. This method significantly improves performance, which is very close to the level of manual correction, and it is also resistant to interference factors such as baseline distortion and noise.

METHODS

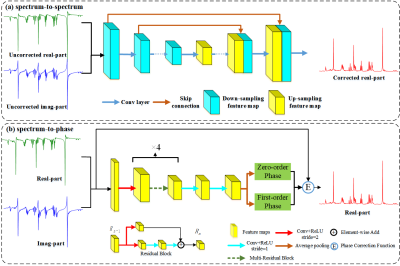
The architecture of the spectra-to-spectra/spectrum-to-phase correction method is shown in Figure 1.
1) The spectrum-to-spectrum correction method constructs a CNN to train the end-to-end mapping using the manually corrected spectrum as the ground truth and the uncorrected spectrum as the input. The network adopts an Unet-like encoder-decoder structure. The structure consists of an encoder to obtain fine-grained multi-scale features by down-sampling and then a decoder to gradually restore the feature details at different scales. The skip connections retain the feature details lost in the down-sampling process. The main process is shown in Figure 1 (a). The overall architecture of Unet includes down-sampling, up-sampling, and jump connection. The red, green, and orange arrows indicate downsampling, upsampling, and jump connection, respectively.
2) The architecture of the spectral-to-phase correction network is shown in Figure 1(b), and the design idea is derived from ResNet. The overall model consists of an initial one-dimensional convolutional layer, four residual blocks and the last two one-dimensional convolutional layers. The first convolutional layer obtains enough local information through a large perceptual field, then uses multiple residual blocks stacked to obtain information of different layers to enhance feature extraction, and finally uses the real part of the output and the ground truth to calculate the loss.
We used a variety of metabolomics data to test the spectrum to spectrum algorithm. Datasets include supernatants of different brain tissue extracts from rats (hereafter referred to as rat brain tissue) and mouse urine collected using a Bruker wave spectrometer. The number of rat brain tissue data is 308, and the original number of sampling points is 8K (8*1024), which is later supplemented to 32K after zero-filling and other operations. 70% of our training is used as the training set, 20% as the validation set, and 10% as the test set. The number of mouse urine data is 470, the original number of sampling points is 8K, and then it is supplemented to 32K after filling zeros and other operations, and the same 70%, 20%, and 10% are divided into training and validation test sets. The true values of all data were manually corrected by experienced operators.

RESULTS

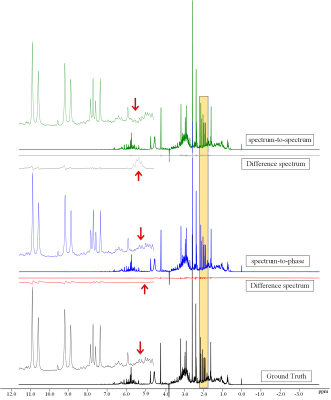
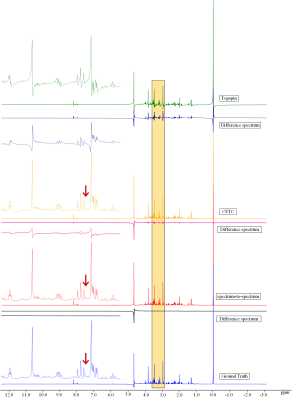
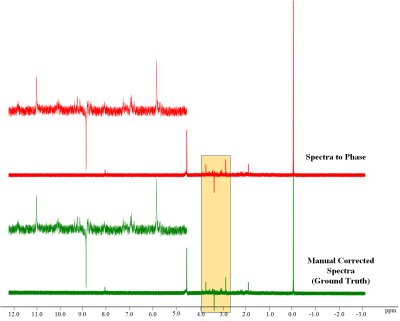
Figure 2 shows the comparison of the spectrum-to-spectrum method and the spectrum-to-phase method. The Figure illustrates that the proposed spectrum-to-phase method can achieve more accurate results, particularly from the difference spectrum.
Figure 3 shows the comparison of the proposed spectrum-to-phase method and other methods (Topspin software and CFTC, a baseline correction algorithm with coarse and fine tuning⁴). It indicates the spectrum-to-phase method achieve better performance. In order to examine the effect of baseline distortion and noise on the algorithm, we simulated a series of baseline distortion data and noisy spectral data to test the robustness of the spectral-to-phase algorithm.
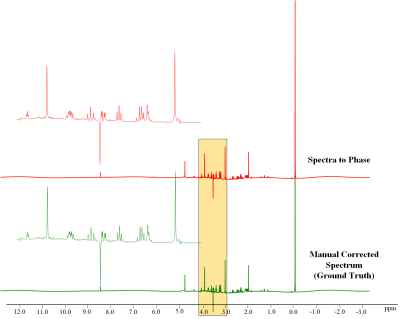
Figure 4 and 5 demonstrate the robustness of the spectrum-to-phase approach in the face of baseline distortion and noise. The results indicate the proposed method can accurately predict the zero- and first-order phases with baseline distortion and noise amplitudes.

DISCUSSION & CONCLUSION

A novel deep learning network (spectral-to-phase method) was proposed for phase correction from magnetic resonance spectrum. The proposed network could achieve phase correction by predicting Ph0 and Ph1. Besides, the method has high robustness. The proposed spectral-to-phase method offered a promising deep learning framework for phase correction benefit from its high quality and high robustness.

Acknowledgements

We gratefully acknowledge the financial support by National Major Scientific Research Equipment Development Project of China (81627901), the National key of R&D Program of China (Grant 2018YFC0115000, 2016YFC1304702), National Natural Science Foundation of China (11575287, 11705274), and the Chinese Academy of Sciences (YZ201677).