4348
Rapid reconstruction of Blip up-down circular EPI (BUDA-cEPI) for distortion-free dMRI using an Unrolled Network with U-Net as Priors1Department of Radiologic Technology, Faculty of Associated Medical Science, Chiang Mai University, Chiang Mai, Thailand, 2National Nanotechnology Center (NANOTEC), National Science and Technology Development Agency (NSTDA), Pathum Thani, Thailand, 3Department of Radiology, Stanford University, Stanford, CA, United States, 4Department of Radiology, Stanford University, Stanford, Stanford, CA, United States, 5Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 6Athinoula A. Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 7Department of Radiology, Harvard Medical School, Boston, MA, United States, 8Department of Electrical Engineering, Stanford University, Stanford, CA, United States, 9Department of Bioengineering, Stanford University, Stanford, CA, United States
Synopsis
Blip-up and Blip-down EPI (BUDA) is a rapid, distortion-free imaging method for diffusion-imaging and quantitative-imaging. Recently, we developed BUDA-circular-EPI (BUDA-cEPI) to shorten the readout-train and reduce T2* blurring for high-resolution applications. In this work, we further improve encoding efficiency of BUDA-cEPI by leveraging partial-Fourier in both phase-encode and readout directions, where complimentary conjugate k-space information from the blip-up and blip-down EPI-shots and S-LORAKS constraint are used to effectively fill-out missing k-space. While effective, S-LORAKS is computationally expensive. To enable clinical deployment, we also proposed a machine-learning reconstruction derived from RUN-UP (unrolled K-I network) that accelerates reconstruction by >300x.
INTRODUCTION
Blip-up and Blip-down EPI acquisition (BUDA)1 is a rapid distortion-free imaging method that has been successfully utilized in diffusion imaging2 and quantitative imaging3. The joint reconstruction in BUDA-EPI across the two blip-up and -down EPI-shots is performed using structured low-rank constraint4,5 to provide robustness to shot-to-shot phase variation, at a cost of lengthy reconstruction. Recently, fast deep-learning reconstruction approaches have been proposed for conventional multi-shot EPI and demonstrated to provide high quality reconstructions6,7. In this work, the RUN-UP7, which utilizes an unrolled K-I network with U-Net as priors, is adopted and modified for use in BUDA-EPI as well as in a new BUDA-circular-EPI (BUDA-cEPI) acquisition8,9. BUDA-cEPI employs circular k-space sampling for a shorter readout train, to reduce T2* blurring for sharper high-resolution imaging. A method for further readout shortening is also proposed in this work using a combined PE&RO partial Fourier (pF) encoding, where complimentary conjugate k-space information from the blip-up and blip-down EPI-shots and S-LORAKS constraint are used to effectively fill-out missing k-space to generate ground-truth data for training our modified RUN-UP reconstruction. Our proposed BUDA-cEPI with RUN-UP reconstruction was demonstrated to enable sharp and distortion-free EPI-based imaging with fast and robust reconstruction.METHODS
I.Single Polarity Circular EPI Signal Model: With a short echo-spacing ($$$T_{es}$$$) the off-resonance effects is primarily along the phase-encoding (PE) direction. After odd-even echo phase shift correction, the signal at readout $$$m\in[0\;M\!-1]$$$ of PE line $$$n\in[0\;N\!-\!1]$$$ can be modeled as:$$g_{c}[m,n]=\sum_{l=0}^{N\!-\!1}\left\{\sum_{p=0}^{P\!-1}\sum_{q=0}^{Q\!-1}s_c[p,q]u[p,q]e^{(-j(k_{x}[m]p+k_{y}[n]q)}\right\}+ε_{c}[m,n]\;\;\;\;(1)$$
$$$p\in[0\;P\!-1]$$$ and $$$q\in[0\;Q\!-1]$$$ are pixel indices. $$$u$$$ is the underlying image, $$$k_{x}$$$ and $$$k_{y}$$$ are the k-space coordinates in the readout and phase-encoding dimensions. $$$s_c$$$ is the sensitivity profile for coil $$$c\in[0\;C\!-1]$$$, $$$Δw_0$$$ is the off-resonance, and $$$ε$$$ is white Gaussian noise. Defining Defining $$$W_l=diag\{e^{-j(Δw_0[p,q]{l-[\frac{N\!-1}{2}]}T_{es}}\}$$$ and $$$S=[diag{S_0}⋯diag{S_{C\!-1}}]^T$$$, Eq. (1) abstracts to:
$$G=\left(I\otimes\sum_0^{N-1}FW_l\right)Su+\epsilon=Au+\epsilon\;\;\;\;(2)$$where is the Fourier transform $$$F$$$ and $$$\otimes$$$ is Kronecker’s product
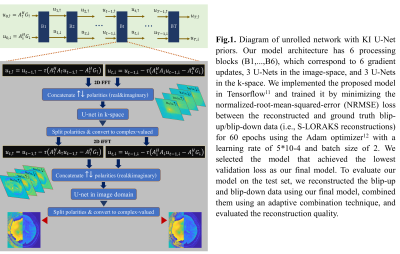
II.Joint Blip-up and Blip-down Reconstruction with Unrolled Network: As opposed Eq. (2) which has a single matrix $$$A$$$, BUDA circular EPI can be described using two forward matrices: $$$A_\uparrow$$$ for the blip-up and $$$A_\downarrow$$$ for the blip-down acquisitions. To reconstruct the underlying data $$$u_\uparrow$$$ and $$$u_\downarrow$$$ from the corresponding acquired k-space data $$$A_\uparrow$$$ and $$$A_\downarrow$$$, we solve the following optimization problem:
$$\min_{u_\uparrow,u_\downarrow}\frac{1}{2}\left\|\begin{bmatrix}A_\uparrow&0\\0&A_\downarrow\end{bmatrix}\begin{bmatrix}u_\uparrow\\u_\downarrow\end{bmatrix}-\begin{bmatrix}G_\uparrow\\G_\downarrow\end{bmatrix}\right\|_2^2+R(u_\uparrow,u_\downarrow)\;\;\;\;(3)$$
where $$$R(u_\uparrow,u_\downarrow)$$$ is a regularization term that is modeled using multiple U-Nets10. Extending the KI-Net method in the RUN-UP7 to the BUDA circular EPI formulation, we develop a joint reconstruction algorithm (Fig.1) that has two main components: simple gradient updates in the image-space and a regularization in both k- and image-spaces. While we use complex-valued operations for the gradient updates, we use real-valued operations for the regularization component. We represent the complex-valued data pair ($$$u_\uparrow,u_\downarrow$$$)as single real-valued data with 4 artificial channels, corresponding to $$$Re\{u_\uparrow\}$$$, $$$Im\{u_\uparrow\}$$$, $$$Re\{u_\downarrow\}$$$ and $$$Im\{u_\downarrow\}$$$, before passing them to the U-Nets. As shown in Fig.1.
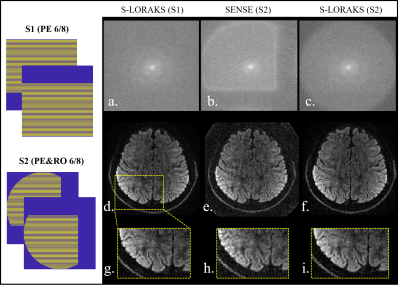
III.Data Acquisition and Processing: In-vivo experiments were performed on a 3T GE Premier equipped with a 48-channel receiver head coil (SVD-compressed to12-channel). Six healthy volunteers were scanned after informed consent according to IRB protocol. In one volunteer, BUDA-EPI data were acquired at 1.25×1.25×2.00 mm. resolution with pF 6/8 and b-value-1000. To characterize the achievable reconstruction of BUDA-cEPI, the reconstruction of this BUDA-EPI data was compared to one from a synthesized BUDA-cEPI data with 6/8 pF along both RO & PE obtained from cropping this dataset, where S-LORAKS was used for both reconstructions. On the other five volunteers, BUDA-cEPI DWI data (10-NEX of b-value 0, 1-NEX with 50 directions of 1000 mm.2/sec.) were acquired with following parameters: matrix 300×300 pixels, resolution 0.73×0.73×5.00 mm., 16 slices, SENSE-factor of 4, and partial Fourier of 5/8 along both RO and PE. Low resolution gradient echo imaging was also performed to acquire calibration data, which is used for estimating coil sensitivity maps using ESPIRiT13. The ground-truth data were prepared from 4 subjects using S-LORAKS. Preliminarily, only 587 and 120 slices whole brain coverage from 4 subjects were used to train and validate the network, respectively. Data from the 5th subject were used for testing.
RESLUTS
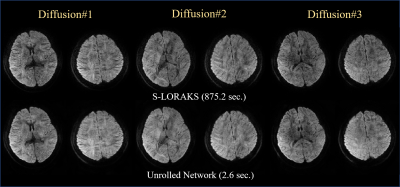
Fig. 2 shows the comparison between BUDA-EPI and synthesized BUDA-cEPI, where Naïve SENSE reconstruction of BUDA-cEPI resulted in the inability to recover the missing pF data (2b) and blurry image (2h). S-LORAKS enables to recover such missing k-space data efficiently as illustrated in the enlarged image (2i). Fig. 3 shows preliminary results comparing S-LORAKS vs. RUN-UP reconstructions of BUDA-cEPI data at 0.73 in-plane resolution across different diffusion encodings at b1000 mm2/sec, where similarly high-quality reconstructions can be obtained. The S-LORAKS reconstruction took 872s while RUNUP took 2.6s, which represent > 300x speedup.DISCUSSIONS
In this work, we developed a new reconstruction approach based on S-LORAKS and RUNUP unrolled-reconstruction, to enable high quality reconstruction of BUDA-cEPI with dual RO&PE pF encodings in the present of shot-to-shot phase variations in diffusion imaging. Preliminary results indicate that high-quality sharp diffusion images free of distortion can be obtained in a fast reconstruction time. Future work will focus on further training and validation of the proposed reconstruction on a larger dataset and rigorous quantification of the reconstruction performance on error metrics derived from the reconstructed images as well as extracted diffusion parameters.Acknowledgements
This study is supported in part by GE Healthcare research funds and NIH R01EB020613, R01MH116173, R01EB019437, U01EB025162 , P41EB030006.References
1. Bilgic B, Chatnuntawech I, Manhard MK, et al. Highly accelerated multishot echo planar imaging through synergistic machine learning and joint reconstruction. Magn Reson Med. 2019; 82:1343- 1358
2. Liao C, Bilgic B, Tian Q, Stockmann JP, Cao X, Fan Q, Iyer SS, Wang F, Ngamsombat C, Lo WC, Manhard MK, Huang SY, Wald LL, Setsompop K. Distortion-free, high-isotropic-resolution diffusion MRI with gSlider BUDA-EPI and multicoil dynamic B0 shimming. Magn Reson Med. 2021; 86(2): 791-803.
3. Cao X, Wang K, Liao C, Zhang Z, Srinivasan Iyer S, Chen Z, Lo WC, Liu H, He H, Setsompop K, Zhong J, Bilgic B. Efficient T2 mapping with blip-up/down EPI and gSlider-SMS (T2 -BUDA-gSlider). Magn Reson Med. 2021; 86(4): 2064-2075
4. Haldar JP. Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI. IEEE Trans Med Imaging. 2014; 33(3): 668-81.
5. Mani M, Jacob M, Kelley D, Magnotta V. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn Reson Med. 2017; 78(2): 494-507.
6. Aggarwal H, Mani M, and Jacob M. Multi-shot sensitivity-encoded diffusion MRI using model-based deep learning (MODL-MUSSELS). arXiv preprint arXiv:1812.08115, 2018.
7.Hu, Y, Xu, Y, Tian, Q, et al. RUN-UP: Accelerated multishot diffusion-weighted MRI reconstruction using an unrolled network with U-Net as priors. Magn Reson Med. 2020; 85: 709– 72.
8. Congyu ISMRM 2022
9. Rettenmeier C, Maziero D, Qian Y, Stenger VA. A circular echo planar sequence for fast volumetric fMRI. Magn Reson Med. 2019; 81(3):1685-1698.
10. O. Ronneberger, P. Fischer, and T. Brox, “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical image computing and computer-assisted intervention, (2015), pp. 234–241.
11. Abadi M., Barham P., Chen J. et al. TensorFlow: A System for Large-Scale Machine Learning. OSDI , 16, page 265-283. (2016).
12. Kingma D, Ba J, Adam: a method for stochastic optimization, Proc. Int. Conf. Learn. Represent. 2015 1–41.
13. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014; 71: 990– 1001.
Figures