4347
Low-rank Parallel Imaging Reconstruction Imbedded with a Deep Learning Prior Module1Laboratory of Biomedical Imaging and Signal Processing, The University of Hong Kong, Hong Kong, China, 2Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong, China
Synopsis
Recently, deep learning methods have shown superior performance on image reconstruction and noise suppression by implicitly yet effectively learning prior information. However, end-to-end deep learning methods face the challenge of potential numerical instabilities and require complex application specific training. By taking advantage of the multichannel spatial encoding (as exploited by conventional parallel imaging reconstruction) and prior information (exploited by deep learning methods), we propose to embed a deep learning module into the iterative low-rank matrix completion based image reconstruction. Such strategy significantly suppresses the noise amplification and accelerates iteration convergence without image blurring.
Introduction
Existing parallel imaging often suffers from artifacts and severe noise amplification when reconstructing highly undersampled k-space. Certain prior information such as limited spatial support, transform sparsity representation (e.g., wavelet transform) and smoothness of coil sensitivity is commonly utilized to constrain the solution space for better reconstructions1,2. Recently, deep learning methods have shown superior performance on image reconstruction and noise suppression by implicitly yet effectively learning prior information3-6. However, end-to-end deep learning methods often face the challenge of potential numerical instabilities and require complex application specific training7. In this study, we propose to embed a deep learning prior module into the low-rank (LR) matrix completion based reconstruction to overcome the limitations of deep learning instabilities while preserving the LR reconstruction stability. The results demonstrate that this strategy can improve LR image reconstruction in terms of better recovering image details, significantly suppressing noise amplification and accelerating the iteration convergence.Method
Low-rank Reconstruction with an Embedded Deep Learning Prior ModuleFor LR reconstruction demonstration, we use the classic simultaneous autocalibrating and k-space estimation2 (SAKE) method to exploit the multi-channel information of k-space by enforcing the low-rankness of the constructed block-wise Hankel matrix. In this study, we embed a deep learning prior module to explore the redundant information and transform sparsity representation from single-channel MR images. As depicted in Figure 1(A), each iteration alternates between promoting low-rankness of constructed block-wise Hankel matrix in k-space and the proposed deep learning prior module. Such 2-step iteration aims to suppress the noise amplification while avoiding the potential numerical instabilities that can be associated with end-to-end deep learning methods. We term the proposed method as LR-DL.
Proposed Deep Learning Prior Module
The deep learning prior module builds a nonlinear mapping between the fully-sampled reference image and the fully-sampled noise corrupted image. It is trained on U-Net6,8 with information multi-distillation block9 (IMDB) shown in Figure 1(B). The U-Net contains four scales with an identity skip connection between 2×2 strided convolution (SConv) downscaling and 2×2 transposed convolution (TConv) upscaling for each. This four-scale convolution and deconvolution operation is supposed to extract prior information such as transform sparsity representations. Four successive IMDBs are used in each scale with three 3×3 convolutions followed by a Leaky ReLU in each IMDB. Two-part features are extracted by channel split. For simplicity and generalization, the noise corrupted images are simulated by adding complex-valued Gaussian noise with different levels.
In this study, 3T T1w 3D GRE brain data with 1mm isotropic resolution from Calgary-Campinas Public Brain MR Database10 were used for training and testing with compressed 6 channels11. The acquisition parameters were TR/TE/TI=6.3/2.6/400 ms and matrix size=226×218×170. Axial images from 57 and 10 subjects with a matrix size of 226×218 were employed for training and testing, respectively. Here, SNRs of simulated noisy images for training ranged from 15 to 20 dB. The real and imaginary parts of images were treated as two input channels of U-Net. The training was carried out by optimizing mean absolute error using Adam with a batch size of 16 and an initial learning rate of 1×10-4 over 30 iterations, which took approximately 6 hours on an NVIDIA RTX 8000 GPU.
Performance Evaluation
LR-DL was evaluated using retrospectively undersampled k-space with varying undersampling patterns and acceleration factors. The performance of both LR (SAKE) and LR-DL was evaluated by reconstructed images, error maps and their NRMSE, PSNR and SSIM values.
Results
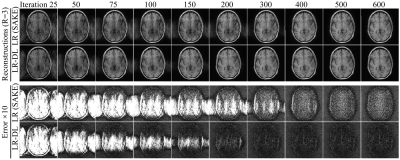
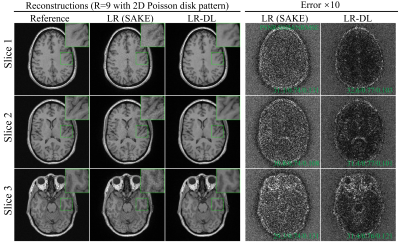
Figure 2 shows reconstructions by LR (SAKE) and LR-DL using 1D random undersampling patterns (without central consecutive lines) along phase encoding (PE) direction at R=2, 3, and 4 from 6-channel data, respectively. LR-DL significantly suppressed the overfitting to noise at high acceleration factors. Meanwhile, LR-DL could reconstruct images with significantly better image details. Noted that the deep learning prior module can be used for various undersampling patterns and acceleration factors without re-training. Figure 3 shows the typical reconstructions from three different slices at R=3 (undersampling pattern identical to that in Figure 2), consistently demonstrating better performance on recovering high-frequency information and suppressing noise amplification. Figure 4 illustrates the interim reconstruction results at different iteration stages. LR-DL clearly accelerated the iteration convergence, again indicating the effectiveness of the proposed deep learning prior module. Figure 5 presents results with 2D Poisson disk pseudo-random undersampling pattern along two PE directions at R=9, where LR-DL exhibited significantly better performance.Discussion and Conclusions
The proposed strategy improves the low-rank parallel imaging reconstruction by an embedded deep learning prior module. It effectively recovers image details and suppresses noise amplification. In contrast to many end-to-end deep learning methods, we use the deep learning network as a tool to learn general prior information and incorporate it to constrain the parallel imaging reconstruction. Furthermore, this strategy is simple since the prior module is trained with fully-sampled image data and can accommodate various 1D/2D undersampling and coil sensitivity variations without re-training. Future studies will explore the potential and benefits of such deep learning prior module in LR reconstruction of multi-slice, multi-contrast and dynamic imaging data12,13, and extend the concept to other iterative MRI reconstruction methods such as compressed sensing1.Acknowledgements
This work was supported in part by Hong Kong Research Grant Council (R7003-19F, HKU17112120 and HKU17127121 to E.X.W., and HKU17103819, HKU17104020 and HKU17127021 to A.T.L.L.), Lam Woo Foundation, and Guangdong Key Technologies for Treatment of Brain Disorders (2018B030332001) to E.X.W.References
[1] Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58:1182-1195.
[2] Shin PJ, Larson PEZ, Ohliger MA, Elad M, Pauly JM, Vigneron DB, Lustig M. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn Reson Med 2014;72:959-970.
[3] Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, Knoll F. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med 2018;79:3055-3071.
[4] Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS. Image reconstruction by domain-transform manifold learning. Nature 2018;555:487-492.
[5] Polak D, Cauley S, Bilgic B, Gong E, Bachert P, Adalsteinsson E, Setsompop K. Joint multi-contrast variational network reconstruction (jVN) with application to rapid 2D and 3D imaging. Magn Reson Med 2020;84:1456-1469.
[6] Zhang K, Li Y, Zuo W, Zhang L, Van Gool L, Timofte R. Plug-and-play image restoration with deep denoiser prior. IEEE T Pattern Anal 2021.
[7] Antun V, Renna F, Poon C, Adcock B, Hansen AC. On instabilities of deep learning in image reconstruction and the potential costs of AI. In: Proceedings of the National Academy of Sciences, 2020, p 30088.
[8] Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. In: International Conference on Medical image computing and computer-assisted intervention, 2015, Springer, p 234-241.
[9] Hui Z, Gao X, Yang Y, Wang X. Lightweight image super-resolution with information multi-distillation network. In: Proceedings of the 27th ACM International Conference on Multimedia, 2019, p 2024-2032.
[10] Souza R, Lucena O, Garrafa J, Gobbi D, Saluzzi M, Appenzeller S, Rittner L, Frayne R, Lotufo R. An open, multi-vendor, multi-field-strength brain MR dataset and analysis of publicly available skull stripping methods agreement. NeuroImage 2018;170:482-494.
[11] Buehrer M, Boesiger P, Kozerke S. Virtual body coil calibration for phased-array imaging. In: Proceedings of the 17th Annual Meeting ISMRM, Hawaii, USA, 2009, p 760.
[12] Liu Y, Yi Z, Zhao Y, Chen F, Feng Y, Guo H, Leong ATL, Wu EX. Calibrationless parallel imaging reconstruction for multislice MR data using low-rank tensor completion. Magn Reson Med 2021;85:897-911.
[13] Yi Z, Liu Y, Zhao Y, Xiao L, Leong ATL, Feng Y, Chen F, Wu EX. Joint calibrationless reconstruction of highly undersampled multicontrast MR datasets using a low-rank Hankel tensor completion framework. Magn Reson Med 2021;85:3256-3271.
Figures
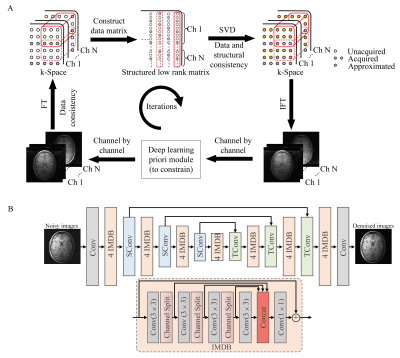
Figure 1 (A) Diagram of iterative low-rank reconstruction with an embedded deep learning prior module (LR-DL). (B) The deep learning prior module trained on U-Net with information multi-distillation block (IMDB). The U-Net contains four scales with 2×2 strided convolution (SConv) downscaling and 2×2 transposed convolution (TConv) upscaling for each. The number of channels for U-Net from the first to the fourth scale is 64,128, 256 and 512, respectively. The kernel size is 3×3 for all convolutions except for IMDBs. IMDB contains three 3×3 convolutions followed by a Leaky ReLU.
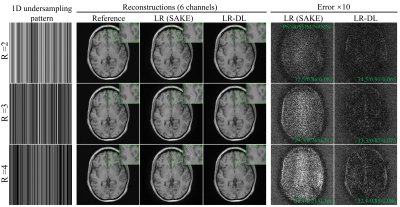
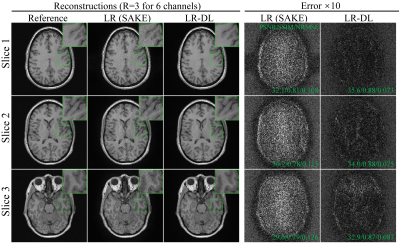
Figure 3 Typical reconstructions of 6-channel T1w GRE data from three different slices at R=3 along PE direction (undersampling pattern identical to that in Figure 2). LR-DL consistently demonstrated better performance on recovering high-frequency information and suppressing noise amplification.