4344
Fast and Calibrationless Low-Rank Reconstruction through Deep Learning Estimation of Multi-Channel Spatial Support1Laboratory of Biomedical Imaging and Signal Processing, The University of Hong Kong, Hong Kong SAR, China, 2Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong SAR, China, 3Department of Electrical and Electronic Engineering, Southern University of Science and Technology, Shenzhen, China
Synopsis
In traditional parallel imaging, calibration data need to be acquired, prolonging data acquisition time or/and sometimes increasing the susceptibility to motion. Low-rank parallel imaging has emerged as a calibrationless alternative that formulates reconstruction as a structured low-rank matrix completion problem while incurring a cumbersome iterative reconstruction process. This study achieves a fast and calibrationless low-rank reconstruction by estimating high-quality multi-channel spatial support directly from undersampled data via deep learning. It offers a general and effective strategy to advance low-rank parallel imaging by making calibrationless reconstruction more efficient and robust in practice.
Introduction
Calibrationless parallel imaging reconstruction, such as low-rank modeling of local k-space neighborhoods (LORAKS1) method, inherently exploits finite image support together with coil sensitivity information (characterized as multi-channel spatial support of MR images) by identifying null-space basis2,3 and approximating undersampled data within a structured low-rank matrix in a sequentially iterative manner. However, this slow iteration process is computationally demanding and can cause reconstruction inaccuracy at high acceleration, significantly compromising applications of calibrationless reconstruction especially for high-resolution imaging with a volume coverage. Using fully sampled multi-slice datasets from the same MR receiving coil system, we formulate a deep learning framework to directly estimate high-quality multi-channel spatial support from undersampled data, enabling an extremely rapid convergence in subsequent LORAKS reconstruction with more effective reductions of artifacts and noise amplification.Theory and Method
Structured Low-rank Matrix Estimation of Multi-channel Spatial SupportAs revealed in calibrationless low-rank reconstruction1,4,5, finite image support and smooth coil sensitivity modulation lead to the inherent low-rankness of constructed block-wise Hankel matrix. This can be characterized as multi-channel spatial support of MR images and explicitly estimated from the null-space of the structured low-rank matrix (Figure 1A). Specifically, the decomposed null-space vectors are reshaped to sets of convolutional filters, which can inherently null the k-space data. Transforming such nulling filters to image-space and performing the pixel-wise eigen-decomposition would estimate multi-channel spatial support, which contains both finite image support and coil sensitivity information of MR images6,7. Note that multi-channel spatial support derived from undersampled data would be corrupted by artifacts, and thus conventional low-rank reconstruction approach needs to approximate missing samples and estimate more accurate multi-channel spatial support in a cumbersome iterative process.
Deep learning estimation of multi-channel spatial support from undersampled data
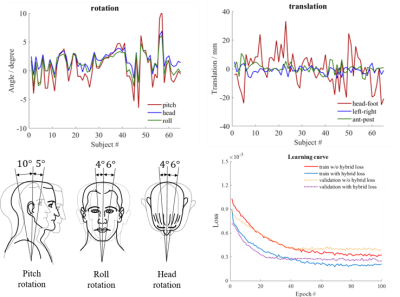
As shown in Figures 1B and 1C, a deep learning framework for directly estimating high-quality multi-channel spatial support is proposed and integrated with LORAKS reconstruction. To extract underlying spatial support from undersampled data, this study exploits correlations of datasets acquired by the same MR coil system through complex-valued convolutional neural networks8 (Figure 1D). To utilize coil-subject geometry parameters available for each dataset, complex-valued networks are trained by minimizing a hybrid loss9 on multi-channel spatial support derived from each dataset with and without spatial alignment to the coil system. Specifically, by performing rigid-body rotation and translation (Figure 2), multi-channel spatial support with minimized variations of coil sensitivity information referred to the same receiving coil system can be obtained for each dataset. Here, $$$λ_{1}$$$ and $$$λ_{2}$$$ are the learnable parameters that control the contributions of multi-channel spatial support $$$S$$$ and $$$S_{ref}$$$ derived from datasets with and without spatial alignment $$$M$$$ to the coil system.
$$ |\lambda_{1}(S_{DL}-S) + \lambda_{2}(MS_{DL}-S_{ref})| $$
Data Preparation
The performance of our proposed framework was evaluated using the publically available Calgary-Campinas MR database10, including fully sampled human brain T1-weighted GRE datasets from 67 healthy subjects collected on a 1.5T clinical scanner using a 12-channel head coil. The number of channels was reduced to 6 in implementation by coil combination11. 54, 7, and 6 subjects with 140 consecutive axial slices from each subject were divided as training, validation, and test sets.
Results
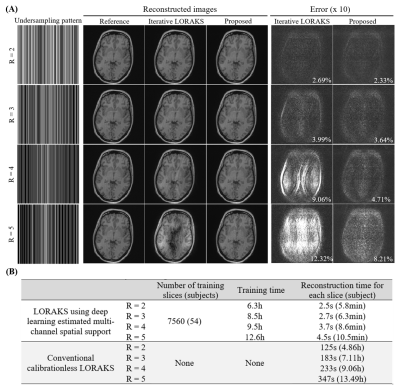
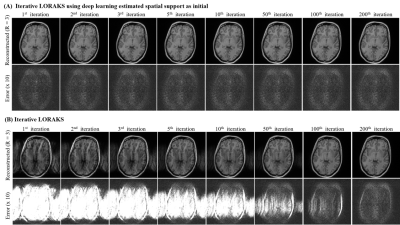
As shown in Figure 3, deep learning directly produced high-quality multi-channel spatial support from undersampled data, whereas those derived after iterative LORAKS reconstruction still exhibited estimation errors in terms of both the magnitude and phase. As a result, deep learning estimation of multi-channel spatial support led to a high-fidelity reconstruction of this slice with more effective artifact reduction at R=4 (Figure 4A). Such improvement was more prominent at even higher acceleration (R=5). Note that noise-like residuals associated with noise propagation and amplification were also significantly suppressed as the acceleration factor increased (R=3-5). For relatively low acceleration (R=2), estimating multi-channel spatial support via deep learning did not necessarily improve image quality but could substantially reduce the reconstruction time. In general, the proposed deep learning framework enabled almost real-time low-rank reconstruction with ~3s per slice as summarized in Figure 4B, whereas conventional iterative reconstruction required more than 2min for each slice. Figure 5 further illustrates interim results of LORAKS reconstruction with and without initial multi-channel spatial support estimated via deep learning. As demonstrated, extremely rapid convergence at first several iterations is possible by providing such a well-conditioned initial for solving the iterative reconstruction problem.Discussion and Conclusions
This study presents a novel and effective deep learning framework to estimate high-quality multi-channel spatial support for advancing calibrationless low-rank reconstruction while preserving its numerical stability. We expect that the general strategy for improving analytical reconstruction through deep learning is also compatible with other traditional parallel imaging approaches. For instance, the proposed framework can also extend to obtain accurate coil sensitivity maps from undersampled data for SENSE type of reconstruction7,12.Note that learning a nonlinear projection from undersampled data to multi-channel spatial support derived from fully sampled data is highly possible and reasonable due to the smoothness condition of multi-channel spatial support. Further, datasets from the same MR coil system exhibit inherent correlations in coil sensitivity information and can be captured more effectively and efficiently in our proposed framework by incorporating coil-subject geometry parameters, while the majority of existing deep learning reconstruction models have not exploited such spatial geometry information.
Acknowledgements
This work was supported in part by Hong Kong Research Grant Council (R7003-19F, HKU17112120 and HKU17127121 to E.X.W., and HKU17103819, HKU17104020 and HKU17127021 to A.T.L.L.), Lam Woo Foundation, and Guangdong Key Technologies for Treatment of Brain Disorders (2018B030332001) to E.X.W..References
[1] Haldar JP, Zhuo J. P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data. Magn Reson Med 2016;75(4):1499-1514.
[2] Haldar JP, Setsompop K. Linear Predictability in Magnetic Resonance Imaging Reconstruction: Leveraging Shift-Invariant Fourier Structure for Faster and Better Imaging. IEEE Signal Processing Magazine 2020;37(1):69-82.
[3] Zhang J, Liu C, Moseley ME. Parallel reconstruction using null operations: Parallel Imaging Reconstruction. Magn Reson Med 2011;66(5):1241-1253.
[4] Shin PJ, Larson PEZ, Ohliger MA et al. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn Reson Med 2014;72(4):959-970
[5] Lee D, Jin KH, Kim EY, Park SH, Ye JC. Acceleration of MR parameter mapping using annihilating filter-based low rank hankel matrix (ALOHA). Magn Reson Med 2016;76(6):1848-1864.
[6] Yi Z, Zhao Z, Liu Y et al. Fast Calibrationless Image-space Reconstruction by Structured Low-rank Tensor Estimation of Coil Sensitivity and Spatial Support. In: Proceedings of the 29th Annual Meeting of ISMRM, 2021, p 0067.
[7] Uecker M, Lai P, Murphy MJ et al. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71(3):990-1001.
[8] Xiao, L, Liu, Y, Yi, Z, et al. Partial Fourier reconstruction of complex MR images using complex-valued convolutional neural networks. Magn Reson Med. 2021; 00: 1– 16.
[9] Dosovitskiy A, Djolonga J. You only train once: Loss-conditional training of deep networks. In: International Conference on Learning Representations, 2019.
[10] Souza R, Lucena O, Garrafa J et al. An open, multi-vendor, multi-field-strength brain MR dataset and analysis of publicly available skull stripping methods agreement. Neuroimage 2018;170:482-494.
[11] Buehrer M, Pruessmann KP, Boesiger P, Kozerke S. Array compression for MRI with large coil arrays. Magn Reson Med 2007;57(6):1131-1139.
[12] Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med 1999;42(5):952-962.
Figures
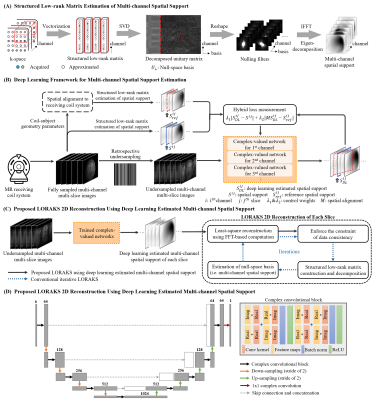
Figure 1. (A) Structured low-rank matrix estimation of multi-channel spatial support. (B) The proposed deep learning framework. To utilize coil-subject geometry parameters, complex-valued networks are trained by minimizing a hybrid loss on spatial support derived from datasets with and without spatial alignment to the coil system. These networks are trained separately for each channel to capture the distinct coil phase characteristic. (C) LORAKS using multi-channel spatial support estimated via deep learning. (D) Network achitecture.