4343
A Microstructural Estimation Transformer with Sparse Coding for NODDI (METSCN)
Tianshu Zheng1, Yi-Cheng Hsu2, Yi Sun2, Yi Zhang1, Chuyang Ye3, and Dan Wu1
1Department of Biomedical Engineering, College of Biomedical Engineering & Instrument Science, Zhejiang University, Hangzhou, Zhejiang, China, Hangzhou, China, 2MR Collaboration, Siemens Healthineers Ltd., Shanghai, China, Shanghai, China, 3School of Information and Electronics, Beijing Institute of Technology, Beijing, China, Beijing, China
1Department of Biomedical Engineering, College of Biomedical Engineering & Instrument Science, Zhejiang University, Hangzhou, Zhejiang, China, Hangzhou, China, 2MR Collaboration, Siemens Healthineers Ltd., Shanghai, China, Shanghai, China, 3School of Information and Electronics, Beijing Institute of Technology, Beijing, China, Beijing, China
Synopsis
Diffusion MRI (dMRI) models play an important role in characterizing tissue microstructures, commonly in the form of multi-compartmental biophysical models that are mathematically complex and highly non-linear. Fitting of these models with conventional optimization techniques is prone to estimation errors and requires dense sampling of q-space. Here we present a learning-based framework for estimating microstructural parameters in the NODDI model, termed Microstructure Estimation Transformer with Sparse Coding for NODDI (METSCN). We tested its performance with reduced q-space samples. Compared with the existing learning-based NODDI estimation algorithms, METSCN achieved the best accuracy, precision, and robustness.
Introduction
Diffusion MRI (dMRI) models are widely used to depict the tissue microstructure[1]. Advanced dMRI, such as NODDI[2], ActiveAX[3], AxCaliber[4] are highly non-linear with complex multi-compartmental configurations. Fitting of these models commonly requires hundreds of samples in the q-space with different b-values and diffusion directions leading to a long acquisition time and fitting is prone to error and instability. Deep learning (DL) techniques have been employed for dMRI model estimation with reduced q-space sampling[5]. However, the common learning-based structure is not related to the biophysical model and is therefore hard to interpret. In this work, we propose a Transformer based network Microstructure Estimation Transformer with Sparse Coding for NODDI (METSCN) to estimate the microstructural parameters. This network links the biophysical model by unfolding the optimization process and incorporating the strength of the Transformer structure in feature extracting. Its performance was compared with other state-of-the-art learning-based algorithms on the public Human Connectome Project (HCP) dataset[6].Methods
The METSCN framework can be divided into two parts: a Transformer encoder and a NODDI decoder.Transformer Encoder:
To accommodate 2D input, the image $$$\mathrm{x}_{0}\in\mathbb{R}^{H\times{W}\times{C}}$$$ (H and W are the height and width of the image, C is the number of channels) is split into smaller 2D patches $$$\mathrm{x}_{p}\in\mathbb{R}^{N\times({H}_{p}\times{W}_{p}\times{C})}$$$ (N is the number of patches) with a non-overlap design. Data are sent to a Layer Normalization (LN) Layer[7] and a multi-head self-attention (MSA) layer. The input of embedded patches and the output from MSA are connected through skip connection. The output is sent to the LN layer and two fully connected layers (Fig. 1a).
NODDI Decoder:
NODDI model: The NODDI model is defined as [2]:
$$A=(1-v_{iso})(v_{ic}A_{ic})+(1-v_{ic})A_{ec})+v_{iso}A_{iso}(1)$$
where A is the normalized diffusion signal, and $$$A_{ic}$$$, $$$A_{ec}$$$,and $$$A_{iso}$$$ represent the signal from the intra-cellular, extra-cellular, and CSF compartments.
Sparse coding: Inspired by AMICO[8], the NODDI model is linearized through sparse-coding:
$$y_{n}=\varphi_{n}x(2)$$
where $$$y_{n}$$$ are the observed signals in $$$y=\left(y_{1},\cdots,y_{n}\right)^{T}$$$ that are normalized with respect to the b0 signal; $$$\varphi_{n}$$$ is a dictionary vector ($$$\varphi_{n}\in\mathbb{R}^{1\times 2j+i}$$$, j corresponds to the length of the discretized $$$v_{ic}$$$ and $$$\kappa$$$ , and the length of $$$v_{iso}$$$ is i ), and x is a vector of the dictionary coefficients ($$$x^{T}\in\mathbb{R}^{1\times{2j+i}}$$$). The dictionary can be established as:
$$\varphi=[\varphi_{ic},\varphi_{\kappa},\varphi_{iso}](3)$$
$$x=[x_{ic},x_{\kappa},x_{iso}]^{T}(4)$$
According to (1), the three parameters can be reformulated:
$$v_{iso}=\sum{x}_{iso}^{i}(5)$$
$$v_{ic}=\frac{\sum\varphi_{ic}^{j}{x}_{i c}^{j}}{\sum{x}_{i c}^{j}}(6)$$
$$\kappa=\frac{\sum\varphi_{\kappa}^{j}x_{k}^{j}}{\sum{x}_{\kappa}^{j}}(7)$$
$$OD=\frac{2}{\pi}arctan(\frac{1}{\kappa})(8)$$
Network construction: The Iterative Hard Thresholding (IHT) method [9] is used to solve this sparse reconstruction problem based on an iterative process:
$$x^{n+1}=H_{M}[{\varphi}^{H}y+(I-{\varphi}_{n}^{H}{\varphi}_{n}){x}^{n}](9)$$
where, $$$H_{M}$$$ denotes the nonlinear operator. Then the NODDI decoder is constructed as Fig. 1b. The complete network is shown in Fig. 1c.
Materials: NODDI data were obtained from the HCP dataset, including 26 brains acquired with 3 b-shells (b=1000, 2000, 3000$$$s/mm^{2}$$$) and 90 directions per shell on 3T Connectome scanner. We selected a subset of 30 gradient directions per b-shell as the training data.
Training and testing: The dataset was split into 5 for training, 5 for validation, and 16 for testing. The gold standard was calculated by the NODDI Matlab toolbox [2] using all diffusion directions. The network was trained using Adam as the optimizer with the total epochs of 2000 and batch size of 512. A reducing learning rate was used with an initial learning rate of $$$1\times{10}^{-4}$$$.
Evaluation methods and criteria: We compared METSCN with other algorithms including 1 dictionary-based method AMICO and 3 learning-based methods q-DL[5], MEDN[10], and MEDN+[11] in terms of accuracy, precision, and robustness. Accuracy is evaluated by the estimation error with respect to the gold standard, while precision is defined as the standard deviation of the estimation results by 3 rounds of bootstrap of diffusion directions. Robustness is achieved by adding abnormal signals to the signal patch by smearing the patch or adding abrupt noise, and testing whether the METSCN will give fake outputs that are not supported by data[12].
Results
Accuracy test: METSCN estimated parameter maps and error maps respected to gold standard were compared with others in Fig. 2. The learning-based methods showed higher accuracy than AMICO, and the model-based structures MEDN, MEDN+, and METSCN showed higher accuracy than the model-free structure q-DL. Transformer-based structure METSCN outperformed the other structures (Table 1).Precision test: Among the model-based learning methods, METSCN showed higher precision than MEDN and MEDN+ based on the standard deviations from bootstrap. While the precision of METSCN was slightly lower than the model-free q-DL (Fig. 2).
Robustness test: Fig. 4 showed the smearing of the input signals resulted in smeared estimation results and abrupt noise added to the input signals led to noisy fitting results, indicating the METSCN-based estimation will not generate erroneous parameters.
Discussion and Conclusion
In this study, we showed that the proposed METSCN achieved accurate and precise NODDI parameters estimation with high robustness using only a subset of q-space data, and thus could be potentially used to accelerate NODDI acquisition. This is the first time the Transformer structure has been used for NODDI model parameter estimation which can enable the precision and accuracy of the estimation. The proposed model-driven network incorporated the underlying NODDI model in the network design, which enhances its performance. Further work should evaluate this structure on other advanced diffusion models, such as ActiveAX.Acknowledgements
Ministry of Science and Technology of the People’s Republic of China (2018YFE0114600), National Natural Science Foundation of China (61801424, 81971606, 82122032), and Science and Technology Department of Zhejiang Province (202006140).References
[1] S. Mori and J. Zhang, “Principles of Diffusion Tensor Imaging and Its Applications to Basic Neuroscience Research,” Neuron, vol. 51, no. 5, pp. 527–539, 2006, doi: 10.1016/j.neuron.2006.08.012.[2] H. Zhang, T. Schneider, C. A. Wheeler-Kingshott, and D. C. Alexander, “NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain,” Neuroimage, vol. 61, no. 4, pp. 1000–1016, 2012, doi: 10.1016/j.neuroimage.2012.03.072.
[3] D. C. Alexander et al., “Orientationally invariant indices of axon diameter and density from diffusion MRI,” Neuroimage, vol. 52, no. 4, pp. 1374–1389, 2010, doi: 10.1016/j.neuroimage.2010.05.043.
[4] Y. Assaf, T. Blumenfeld-Katzir, Y. Yovel, and P. J. Basser, “AxCaliber: A method for measuring axon diameter distribution from diffusion MRI,” Magn. Reson. Med., vol. 59, no. 6, pp. 1347–1354, 2008, doi: 10.1002/mrm.21577.
[5] V. Golkov et al., “q-Space Deep Learning : Twelve-Fold Shorter and Model-Free Diffusion MRI Scans,” vol. 35, no. 5, pp. 1344–1351, 2016.
[6] D. C. Van Essen, S. M. Smith, D. M. Barch, T. E. J. Behrens, E. Yacoub, and K. Ugurbil, “The WU-Minn Human Connectome Project: An overview,” Neuroimage, vol. 80, pp. 62–79, 2013, doi: https://doi.org/10.1016/j.neuroimage.2013.05.041.
[7] J. L. Ba, J. R. Kiros, and G. E. Hinton, “Layer Normalization,” 2016, [Online]. Available: http://arxiv.org/abs/1607.06450.
[8] A. Daducci, E. J. Canales-Rodríguez, H. Zhang, T. B. Dyrby, D. C. Alexander, and J. P. Thiran, “Accelerated Microstructure Imaging via Convex Optimization (AMICO) from diffusion MRI data,” Neuroimage, vol. 105, pp. 32–44, 2015, doi: 10.1016/j.neuroimage.2014.10.026.
[9] T. Blumensath and M. E. Davies, “Iterative hard thresholding for compressed sensing,” Appl. Comput. Harmon. Anal., vol. 27, no. 3, pp. 265–274, 2009, doi: 10.1016/j.acha.2009.04.002.
[10] C. Ye, “Estimation of Tissue Microstructure Using a Deep Network Inspired by a Sparse Reconstruction Framework,” in Information Processing in Medical Imaging, 2017, pp. 466–477.
[11] C. Ye, “Tissue microstructure estimation using a deep network inspired by a dictionary-based framework,” Med. Image Anal., vol. 42, pp. 288–299, 2017, doi: 10.1016/j.media.2017.09.001.
[12] D. Karimi et al., “Deep learning-based parameter estimation in fetal diffusion-weighted MRI,” Neuroimage, vol. 243, no. August, p. 118482, 2021, doi: 10.1016/j.neuroimage.2021.118482.
Figures
Fig.1 Architecture of the proposed Microstructure Estimation Transformer with Sparse Coding for NODDI (METSCN). (a) The Transformer encoder is constructed without position encoding but additional skip connections. (b) The NODDI decoder is designed by unfolding the optimization process corresponding to the IHT process. (c) Network overview.
Fig.2 The gold standard, estimated parameter maps, and error map of Vic (a), Viso (b), and OD (c). The gold standard was estimated by Matlab NODDI toolbox with the full-dataset and the estimated parameters were obtained from AMICO, q-DL, MEDN, and MEDN+, respectively, using reduced q-space samples (30 out of 90). The proposed algorithm demonstrated a more accurate fitting with lower errors than other algorithms.
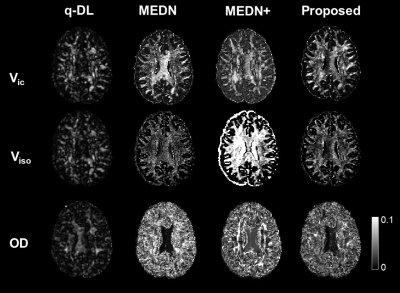
Fig.3 Evaluation of precision on four learning-based algorithms. The proposed method showed higher precision than the other model-based methods MEDN and MEDN+, indicated by the lower standard deviation from bootstrap; but slightly lower than the end-to-end q-DL method.
Fig. 4 Evaluation of robustness by testing whether the proposed method will generate fake output that is not supported by the data. The signal patch in the red rectangle is smeared (a) or noised corrupted (b). Both results demonstrated the network will not produce the unsupported estimation.
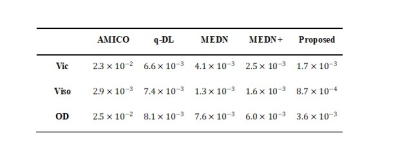
Table 1 The mean square errors (MSE) of four state-of-the-art algorithms AMICO, q-DL, MEDN, and MEDN+ in estimating NODDI parameters compared to the proposed method. The proposed method resulted in lower MSE and thus higher estimation accuracy.
DOI: https://doi.org/10.58530/2022/4343