4338
Noise2Average: deep learning based denoising without high-SNR training data using iterative residual learning1Department of Biomedical Engineering, Tsinghua University, Beijing, China, 2Athinoula A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital, Charlestown, MA, United States, 3Harvard Medical School, Boston, MA, United States, 4Nuffield Department of Clinical Neurosciences, Oxford University, Oxford, United Kingdom, 5Department of Engineering Physics, Tsinghua University, Beijing, China
Synopsis
The requirement for high-SNR reference data reduces the feasibility of supervised deep learning-based denoising. Noise2Noise addresses this challenge by learning to map one noisy image to another repetition of the noisy image but suffers from image blurring resulting from imperfect image alignment and intensity mismatch for empirical MRI data. A novel approach, Noise2Average, is proposed to improve Noise2Noise, which employs supervised residual learning to preserve image sharpness and transfer learning for subject-specific training. Noise2Average is demonstrated effective in denoising empirical Wave-CAIPI MPRAGE T1-weighted data (R=3×3-fold accelerated) and DTI data and outperforms Noise2Noise and state-of-the-art BM4D and AONLM denoising methods.
Introduction
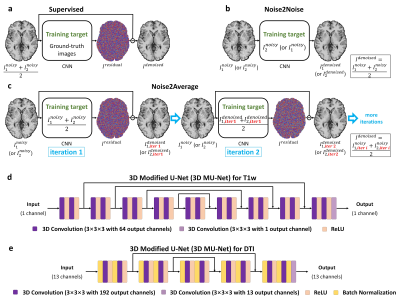
Image denoising benefits MRI data acquired with high acceleration factor and spatial resolution which suffer from intrinsic low signal-to-noise ratio (SNR). Supervised deep learning-based denoising using convolutional neural networks (CNNs) (Fig.1a) has been demonstrated to outperform conventional benchmark methods1,2. Nevertheless, the requirement for high-SNR data as the training target significantly reduces their practical feasibility and generalizability.Noise2Noise3 was recently proposed to address this challenge, which trains a CNN by learning to map one noisy image to another repetition of the noisy image (Fig. 1b). The learned CNN parameters remain unchanged if certain statistics of noisy target values match those of clean target values (e.g., the expectation for L2 minimization).
Noise2Noise has a wide range of applications in MRI where repeated data are often acquired (e.g., two repetitions for averaging). Nonetheless, an essential assumption of Noise2Noise, i.e., the two noisy images only differ due to noise, cannot be satisfied in practice due to imperfect image alignment and intensity mismatch, which leads to image blurring, a well-known problem associated with using voxel-wise errors as the loss for training CNNs4.
We propose “Noise2Average” to improve Noise2Noise, which employs residual learning to preserve image sharpness. Noise2Average maps each noisy image to their average by predicting and subtracting residual values (containing noise and differences from all sources) (Fig.1c). Since each denoised image is highly similar to the averaged image, the quality of the average of denoised images is therefore improved (i.e., similar to averaging 2×2 noisy images). The CNN of Noise2Average is trained by fine-tuning a pre-trained CNN using only two noisy images of each individual subject to further increase the feasibility. The subject-specific supervised residual learning is performed iteratively, using the resultant image from the previous iteration as the training target for the current iteration.
We quantitatively evaluate the performance of Noise2Average using simulated and empirical T1-weighted data. We also propose to generate two repetitions of diffusion-weighted images (DWIs) from multi-directional DTI data through diffusion tensor modeling for self-supervised DTI denoising using Noise2Average.
Methods
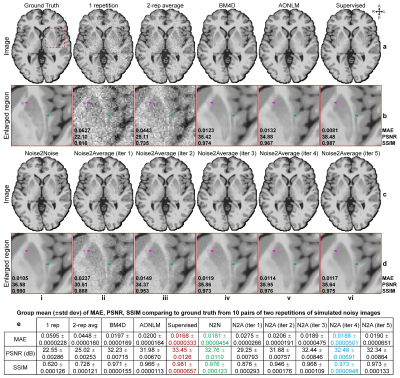
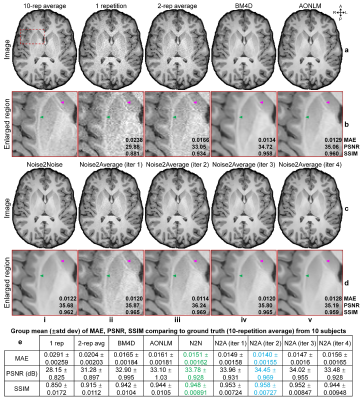
T1-weighted Data. Simulated noisy volumes (30×2 repetitions) were generated by adding Gaussian noise (μ=0, σ=0.5×standard deviation of intensities from brain voxels) to a synthetic T1-weighted MRI volume (1×1×1 mm3, noise-free) obtained from BrainWeb5,6.Wave-CAIPI MPRAGE7-9 data (0.8×0.8×0.8 mm3, 10 repetitions, R=3×3) of 10 healthy subjects (five on Skyra scanner, five on Prisma scanner, Siemens Healthineers) were acquired using 32-channel head coils, with TR/TI/TE=2530/1100/3.65 ms, acquisition time=10×97 s. The 10 repetitions were co-registered and averaged using FreeSurfer’s “mri_robust_template” function as ground-truth data. The first two repetitions were used for denoising.
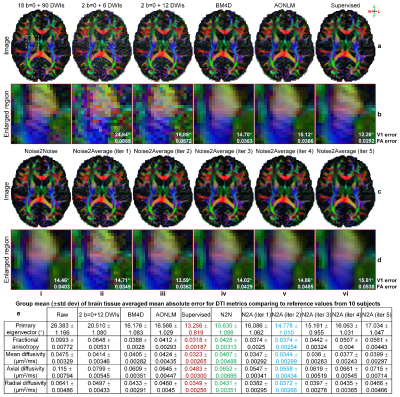
Diffusion data. Pre-processed diffusion data (1.25×1.25×1.25 mm3, 18×b=0, 90×b=1000 s/mm2) of 30 healthy subjects from the Human Connectome Project (HCP)10,11, WU-Minn-Ox Consortium were used. For each subject, 2 b=0 images and 2 subsets of 6 DWIs (i.e., 12 DWIs along uniform directions) were extracted as a DTI dataset for denoising. For each subset of DWIs, diffusion tensors were fitted with the two b=0 volumes and used to synthesize DWIs along all 12 directions. The image synthesis did not amplify noise since diffusion-encoding directions of each subset were optimized to minimize the condition number of diffusion tensor transformation12,13. Thus, two repetitions of 1 b=0 image and 12 DWI volumes were generated. Ground-truth b=0 images were generated as the average of all b=0 images while ground-truth DWIs were synthesized from diffusion tensors fitted using all data.
Denoising. For supervised denoising, MU-Nets (Fig.1d,e) were trained on 20×2 repetitions of simulated T1-weighted volumes and diffusion data from 20 HCP subjects. For Noise2Noise and Noise2Average, MU-Nets (Fig.1d,e) were trained for each pair of noisy images by fine-tuning MU-Nets pre-trained on large datasets (i.e., MPRAGE data at 0.7×0.7×0.7 mm3 with simulated Gaussian noise of 20 subjects from WU-Minn-Ox HCP, and diffusion data at 1.5×1.5×1.5 mm3 of 35 subjects from MGH-USC HCP14) for 10 epochs (per iteration). Training was performed using Tensorflow software with Adam optimizers (L2 loss for T1w and L1 loss for DTI) on 80×80×80 image blocks.
Data were also denoised using conventional benchmark methods (BM4D15,16, AONLM17).
Evaluation. The mean absolute error (MAE), peak SNR (PSNR) and structural similarity index (SSIM) were used to quantify the image similarity comparing to ground-truth images. Averaged MAEs within the brain tissue of five DTI metrics (primary eigenvectors, fractional anisotropy, mean/axial/radial diffusivity) comparing to ground-truth values from tensors fitted using all data were computed.
Results
Supervised denoising performed best for all evaluated data (Figs.2,4,5).Noise2Noise and Noise2Average outperformed BM4D and AONLM (Figs.2-5). Noise2Noise outperformed Noise2Average for simulated T1-weighted data (Fig.2) where two noisy images were perfectly co-registered, as expected. For empirical T1-weighted and DTI data, Noise2Noise-denoised images were blurry, much smoother than those from Noise2Average (Figs.3-5), with lower image similarity comparing to ground-truth images and lower accuracy in DTI metrics (Fig.5).
The results of Noise2Average from the 2nd iteration were the best for empirical data and became more blurry and less accurate from more iterations since the error in target images at each iteration accumulated.
Discussion and Conclusion
Noise2Average performs effective denoising without need for reference high-SNR data or training data from many subjects, which can be easily and widely used for various MRI applications if two or more repetitions of noisy data are available.Acknowledgements
The T1w data at 0.7 mm isotropic resolution and diffusion data at 1.25 mm isotropic resolution were provided by the Human Connectome Project, WU-Minn-Ox Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; U54-MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University. The diffusion data at 1.5 mm isotropic resolution were provided by the Human Connectome Project, MGH-USC Consortium (Principal Investigators: Bruce R. Rosen, Arthur W. Toga and Van Wedeen; U01-MH093765) funded by the NIH Blueprint Initiative for Neuroscience Research grant; the National Institutes of Health grant P41-EB015896; and the Instrumentation Grants S10-RR023043, S10-RR023401, S10-RR019307.
This work was supported by the National Institutes of Health (grant numbers P41-EB015896, P41-EB030006, U01-EB026996, U01-EB025162, S10-RR023401, S10-RR019307, S10-RR023043, R01-EB028797, R03-EB031175, K99-AG073506), the NVidia Corporation for computing support, and the Athinoula A. Martinos Center for Biomedical Imaging.
References
1. Tian Q, Bilgic B, Fan Q, et al. Improving in vivo human cerebral cortical surface reconstruction using data-driven super-resolution. Cerebral Cortex. 2020;31(1):463-482.
2. Zhang K, Zuo W, Chen Y, Meng D, Zhang L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Transactions on Image Processing. 2017;26(7):3142-3155.
3. Lehtinen J, Munkberg J, Hasselgren J, et al. Noise2Noise: Learning Image Restoration without Clean Data. The International Conference on Machine Learning. 2018:2965-2974.
4. Ledig C, Theis L, Huszár F, et al. Photo-realistic single image super-resolution using a generative adversarial network. Proceedings of the IEEE conference on computer vision and pattern recognition. 2017:4681-4690.
5. Cocosco CA, Kollokian V, Kwan RK-S, Pike GB, Evans AC. Brainweb: Online interface to a 3D MRI simulated brain database. NeuroImage. 1997.
6. Cocosco CA, Kollokian V, Kwan RK-S, Pike GB, Evans AC. BrainWeb: Simulated MRI Volumes for Normal Brain. https://brainweb.bic.mni.mcgill.ca/brainweb/selection_normal.html. Accessed.
7. Polak D, Cauley S, Huang SY, et al. Highly‐accelerated volumetric brain examination using optimized wave‐CAIPI encoding. Journal of Magnetic Resonance Imaging. 2019;50(3):961-974.
8. Polak D, Setsompop K, Cauley SF, et al. Wave‐CAIPI for highly accelerated MP‐RAGE imaging. Magnetic Resonance in Medicine. 2018;79(1):401-406.
9. Longo MGF, Conklin J, Cauley SF, et al. Evaluation of Ultrafast Wave-CAIPI MPRAGE for Visual Grading and Automated Measurement of Brain Tissue Volume. American Journal of Neuroradiology. 2020;41(8):1388-1396.
10. Glasser MF, Sotiropoulos SN, Wilson JA, et al. The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage. 2013;80:105-124. 11. Glasser MF, Smith SM, Marcus DS, et al. The human connectome project's neuroimaging approach. Nature Neuroscience. 2016;19(9):1175-1187.
12. Skare S, Hedehus M, Moseley ME, Li T-Q. Condition number as a measure of noise performance of diffusion tensor data acquisition schemes with MRI. Journal of Magnetic Resonance. 2000;147(2):340-352.
13. Tian Q, Bilgic B, Fan Q, et al. DeepDTI: High-fidelity six-direction diffusion tensor imaging using deep learning. NeuroImage. 2020;219:117017.
14. Fan Q, Witzel T, Nummenmaa A, et al. MGH–USC Human Connectome Project datasets with ultra-high b-value diffusion MRI. NeuroImage. 2016;124:1108-1114.
15. Maggioni M, Katkovnik V, Egiazarian K, Foi A. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE transactions on image processing. 2012;22(1):119-133.
16. Maggioni M, Foi A. Nonlocal transform-domain denoising of volumetric data with groupwise adaptive variance estimation. Computational Imaging X. 2012;8296:82960O.
17. Manjón JV, Coupé P, Martí‐Bonmatí L, Collins DL, Robles M. Adaptive non‐local means denoising of MR images with spatially varying noise levels. Journal of Magnetic Resonance Imaging. 2010;31(1):192-203.
Figures