4336
High efficient Bloch simulation of MRI sequences based on deep learning1Department of Electronic Science, Xiamen University, Xiamen, China, 2MSC Clinical & Technical Solutions, Philips Healthcare, Shenzhen, China, 3Department of Magnetic Resonance Imaging, the First Affiliated Hospital of Zhengzhou University, Zhengzhou University, Zhengzhou, China
Synopsis
To overcome the difficulty of obtaining a large number of real training samples, the utilization of synthetic training samples based on Bloch simulation has become more and more popular in deep learning based MRI reconstruction. However, a large amount of Bloch simulation is usually very time-consuming even with the help of GPU. In this study, a simulation network that receives sequence parameters and contrast templates, was proposed to simulate MR images from different imaging sequences. The reliability and flexibility of the proposed method were verified by distortion correction for GRE-EPI images and T2 maps obtained with overlapping-echo detachment planar imaging.
Introduction
Utilizing synthetic data to train deep neural network (DNN) has been widely employed in the MRI field to alleviate the problem of insufficient real training samples.1-5 However, a large amount of data synthesis based on Bloch simulation often involves a huge amount of calculation, especially for the simulation of a MRI sequence that needs to consider a variety of non-ideal experimental conditions, such as GRE-EPI sequence under an inhomogeneous field. Even for some MRI simulators (such as MRiLab6 and SPROM7) using the parallel computing technology of GPU, the time consumed can still be huge. Herein, Simu-Net, a more efficient Bloch simulation method based on deep learning (DL) for different MRI sequences was proposed. After training, the Simu-Net can simulate the MRI sequence within 9 ms for different sequence parameters, while the conventional method usually takes 10 s or even longer, depending on the complexity of the pulse sequence and the demanded accuracy of simulation.Methods
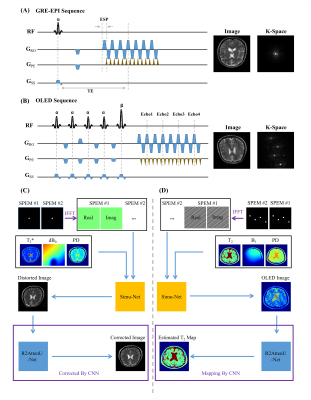
Sequence Parameter Encoding: Different sequence parameters will produce the different MR images. Therefore it is necessary to tell the neural network all the related sequence information. For a specific sequence, it may include dozens of parameters, such as flip angles and phases of RF pulses, evolution durations, and gradient intensities along three directions. How to encode the parameters with high efficiency is rather important for DNN training. We introduced a sequence parameter encoding matrix (SPEM), and then put all the parameters (including flip angles, gradients, echo time, etc.) into the raw SPEM. Inverse Fourier Transform was performed on the raw SPEM to share the encoded sequence parameters in every pixel of image domain, which provided the feasibility for the cropping strategy in data augmentation of DL.Distortion Correction: In GRE-EPI experiments, the inhomogeneous field can distort images in shape and signal intensity. Referenceless distortion correction based on DL has been proposed recently.2 However, generating enough synthetic training samples may take days for a specific sequence with specific parameters. This will greatly impair the flexibility of this correction method. Simu-Net was utilized to speed up this process, as shown in Figure 1C. After the general GRE-EPI Simu-Net was trained, a large number of synthetic training samples quickly produced by Simu-Net was used to train the distortion correction network for the specific sequence parameters.
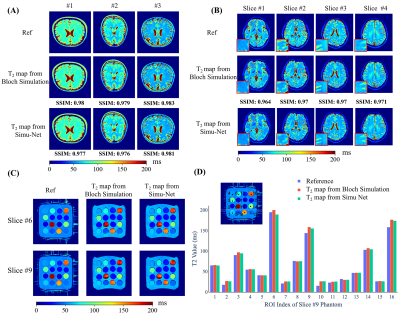
T2 Mapping: The overlapping echo detachment planar imaging (OLED) is a recently proposed single-shot T2 mapping method.1 Because of the complexity of OLED signal, the reconstruction depends on DL technology greatly. After the OLED Simu-Net was trained, a reconstruction network receiving the simulated images from OLED Simu-Net was trained to estimate the T2 maps.
Results and Discussion
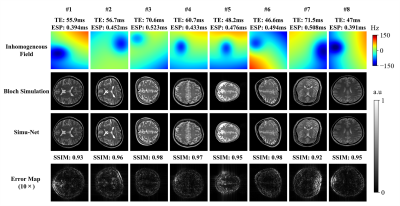
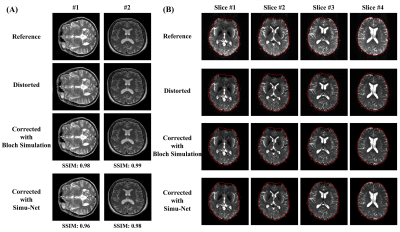
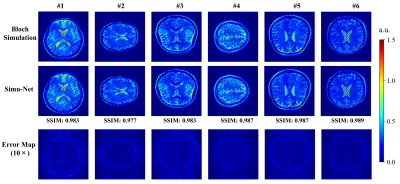
Distortion Correction: Figure 2 shows the simulated results from GRE-EPI Simu-Net under different inhomogeneous fields and sequence parameters. The results from GRE-EPI Simu-Net are quite consistent with the ones by traditional Bloch simulation. To verify the effectiveness of synthetic training samples from GRE-EPI Simu-Net, the distortion correction results of numerical simulation and in vivo human brain experiment are shown in Figure 3. It can be seen that GRE-EPI Simu-Net performs quite well. The corrected results via GRE-EPI Simu-Net are quite consistent with those via traditional Bloch simulation. To produce 20,000 training samples, GRE-EPI Simu-Net took about 4 min, while the traditional Bloch method took about 56 h with the help of GPU, where the acquisition matrix was 128×128 and the numerical template was 512×512.T2 Mapping: Figure 4 shows that the simulated results from OLED Simu-Net are also quite consistent with those from traditional Bloch method. Further, Figure 5 shows the validation of synthetic training samples from OLED Simu-Net via numerical simulation, and water phantom and in vivo human brain experiments. The reconstructed T2 maps from OLED Simu-Net are quite consistent to those from traditional Bloch method, where the SSIM is 0.97. To produce 10,000 training samples, OLED Simu-Net took about 2 min, while the traditional Bloch method took about 47 h with the help of GPU, where the acquisition matrix was 128×128 and numerical template was 512×512.
Conclusion
The proposed DL-based MRI simulator shows high efficiency and excellent performance for two different MRI sequences. Compared with traditional Bloch simulation method, Simu-Net can generate a synthetic training sample in a few milliseconds for different imaging parameters.Acknowledgements
This work was supported in part by the National Natural Science Foundation of China under Grant 82071913 and Grant 11775184, and Science and Technology Project of Fujian Province 2019Y0001.References
1. Cai CB, Wang C, Zeng YQ, et al. Single-shot T2 mapping using overlapping-echo detachment planar imaging and a deep convolutional neural network. Magn Reson Med. 2018;80(5):2202-2214.
2. Liao P, Zhang J, Zeng K, et al. Referenceless distortion correction of gradient-echo echo-planar imaging under inhomogeneous magnetic fields based on a deep convolutional neural network. Comput Biol Med. 2018;100:230-238.
3. Gavazzi S, van den Berg CAT, Savenije MHF, et al. Deep learning-based reconstruction of in vivo pelvis conductivity with a 3D patch-based convolutional neural network trained on simulated MR data. Magn Reson Med. 2020;84(5):2772-2787.
4. Della Maggiora G, Castillo-Passi C, Qiu W, et al. DeepSPIO: Super paramagnetic iron oxide particle quantification using deep learning in magnetic resonance imaging. IEEE Trans Pattern Anal Mach Intell. 2020;PP:1-1.
5. Chen RJ, Lu MY, Chen TY, Williamson DFK, Mahmood F. Synthetic data in machine learning for medicine and healthcare. Nat Biomed Eng. 2021;5(6):493-497.
6. Liu F, Velikina JV, Block WF, Kijowski R, Samsonov AA. Fast realistic MRI simulations based on generalized multi-pool exchange tissue model. IEEE Trans Med Imaging. 2017;36(2):527-537.
7. Cai CB, Lin MJ, Chen Z, Chen X, Cai SH, Zhong JH. SPROM–an efficient program for NMR/MRI simulations of inter- and intra-molecular multiple quantum coherences. C R Phys. 2008;9(1):119-126.
Figures