Introduction

CS using DGM (CS-DGM) emerges as a competitive untrained method for signal reconstruction. Instead of relying on sparse nature, CS-DGM captures the low-level statistics priors of sought solution (i.e., the true signal) by parameterizing it through a carefully designed mapping (generator network) from a low dimensional space to a high dimensional space [1]. In other word, CS-DGM is regularized by the architectures of generator [2]. Theoretically, [3] showed that the recovery error of CS-DGM can be tightly bounded if the coding matrix meets the sub-Gaussian assumption. Most of the time, however, these conditions cannot be met for accelerated MRI, and corresponding theoretical results in CS-DGM are not supported for direct migration to accelerated MRI.
On the other hand, the key to success of CS-DGM is due to its ability to capture image statistics priors. However, in MRI, since there exist basis mismatches between the singularities of true continuous image and discrete grid caused by the discrete or truncated sampling in k-space [4], [5], [6], the image domain statistics priors extraction has deviation. Recent works on k-space interpolation methods have shown that regularization on the true continuous image can be converted to structural low-rank (SLR) regularization in k-space due to the duality between the continuous image domain and k-space [7]. However, the SLR regularization has two shortcomings: firstly, it suffers from high computational burden caused by the singular value decomposition (SVD) of SLR matrices; secondly, it only relies on image structure priors (including multichannel prior, smooth phase and sparsity, e.t.c.) through domain dual transformation without using the statistics priors of k-space. Recent works on DGM have shown that statistics priors can be implicitly captured by the architecture of a carefully designed generator [1], which motivates us to study the k-space DGM.

Theory and method

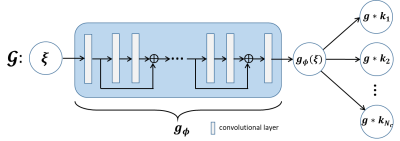
Method: In MRI, the forward model of multichannel k-space data acquisition can be formulated as $$y=\mathcal{M}x+n$$ where $$$y$$$ is under-sampled k-space data and $$$\mathcal{M}$$$ is the sampling pattern. Above problem is attributed to the missing value interpolation problem. Since it is usually ill-conditioned, regularization is essential. Landweber iterative regularization is a effective approach for such problem, which starts from an arbitrary initial point $$${\xi}_{0}$$$ and executes:\begin{equation}\left\{\begin{aligned}{\xi}_{k+1}=&{\xi}_{k}-\mathcal{M}^*(\mathcal{M}x_k-y)\\x_{k+1}=&P_{U}({\xi}_{k+1})\end{aligned}\right.\end{equation}where $$$P_{U}$$$ denotes the orthogonal projection onto subspace $$$U$$$ to capture structure priors of sought solution. In particular, the MR image from the $$$i$$$th coil can be formulated as the product of the coil sensitivities $$${s}_i$$$ and true image $$${f}$$$ and its Fourier transform reads:$$x_i=\widehat{{s}_i{f}}=\widehat{{f}}*\widehat{{s}_i}$$where $$$\widehat{\cdot}$$$ denotes the Fourier transform, $$$*$$$ denotes the convolution operation. Since $$${s}_i$$$ is smooth generally, its Fourier transform $$$\widehat{{s}_i}$$$ decays rapidly. Then, the sought solution $$$x$$$ belongs to a subspace spanned by a vector taken convolution with some small size kernels, i.e.,\begin{equation*}\begin{aligned}U:=\{[x_1,\ldots,x_{N_c}]\in\mathbb{C}^{N\times N_c}|x_i={z}*{k}_i,\forall {z}\in \mathbb{C}^N, {k}_i\in \mathbb{C}^k, k\ll N\}.\end{aligned}\end{equation*} Unfortunately, since $$${z}$$$ and $$${k}_i$$$ are unknown variables, the projection $$$P_{U}$$$ is too computationally expensive to perform.
Inspired by the DGM, we generalize the Landweber iteration to a generator network. Specifically, according to the iterative architecture of Landweber, we generalize the first iteration into a residual network and absorb the unknown variables $$${z}$$$ and $$${k}_i$$$ into network parameters to realize subspace $$$U$$$ projection inexpensively. In particular, the architecture of the generator is depicted in Figure 1. The network $$$\mathcal{G}$$$ is not pre-trained. To make the generated data $$$\mathcal{G}(\xi)$$$ matches the true k-space data, we minimize the following loss function:$$\min_{\mathcal{G}}\|\mathcal{M}\mathcal{G}(\xi)-y\|_F^2.$$
Theory: Let $$$\mathring{\mathcal{G}}:B(s)\rightarrow \mathbb{C}^{N\times N_c}$$$ denote the generator derived from above minimization with architecture depicted in Figure 1. Suppose generator $$$\mathring{\mathcal{G}}$$$ is bounded over $$$B(s)$$$ and the pattern $$$\mathcal{M}$$$ is generated by deterministic or uniformly random sampling. For any $$$x^*\in \mathbb{C}^{N\times N_c}$$$ and observation $$$y = \mathcal{M}x^*+n$$$, let $$$\mathring{\xi}$$$ minimize $$$\|\mathcal{M}\mathring{\mathcal{G}}(\xi)-y\|_F$$$ over $$$B(s)$$$.Then, there exists a constant $$$c>0$$$ such that the reconstruction $$$\mathring{\mathcal{G}}(\mathring{{\xi}})$$$ satisfies:$$\|\mathring{\mathcal{G}}(\mathring{{\xi}})-x^*\|_F\leq\|\widetilde{x}-x^*\|_F+\frac{2\|\mathcal{M}(\widetilde{x}-x^*)\|_F+2\|n\|_F}{c}$$where $$$\widetilde{x}\in \arg\min_{x\in \mathring{\mathcal{G}}(B(s))}\|x-x^*\|_F$$$.

Experiment

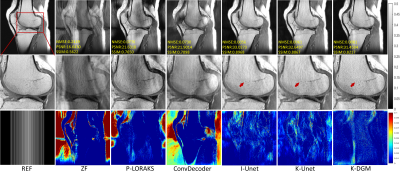
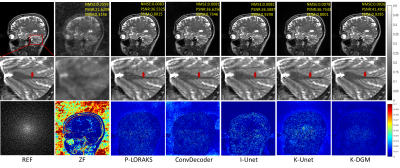
To demonstrate the effectiveness of proposed method,termed k-DGM for simplicity, a series of extensive comparative experiments were studied. We compared our K-DGM with traditional calibration-free SLR regularization method, i.e., P-LORAKS (LORAKS-type=S, algorithm=1 and rank=55) [8],image domain DGM, i.e., ConvDecoder [9], supervised k-space deep learning, i.e., K-Unet [10] and supervised imagedomain deep learning, i.e., I-Unet [11]. The architecture of K-Unet follows that in literature [10] completely. I-Unet is the image domain version of K-Unet where learning is performed on image domain. Comparative experimental results on deterministic and random Patterns are shown in Figure 2 and 3, respectively.
From experimental results, we can know that K-DGM without training is competitive with trained k-space deep learning (K-Unet), image domain deep learning (I-Unet), traditional k-space SLR method (P-LORAKS) and image domain DGM (ConvDecoder) under deterministic and random trajectories.

Conclusion

In this paper, we proposed a novel untrained calibration-free method for k-space interpolation using DGM. Experimentally, we verified that the proposed method outperforms other k-space interpolation method. Theoretically, we proved that our method suffices to guarantee enough accurate interpolations under commonly used sampling patterns. We believe that our method can be a powerful framework for MRI reconstruction when full-sampled data are unaccessible, and its further development of this kind of methods may enable even bigger gains in the future.

Acknowledgements

This work was supported in part by the National Key R&D Program of China (2020YFA0712202, 2017YFC0108802 and 2017YFC0112903); China Postdoctoral Science Foundation under Grant (2020M682990 and 2021M693316); National Natural Science Foundation of China (61771463, 81830056, U1805261, 81971611,61871373, 81729003, 81901736); Natural Science Foundation of Guangdong Province (2018A0303130132); Shenzhen Key Laboratory of Ultrasound Imaging and Therapy (ZDSYS20180206180631473); Shenzhen Peacock Plan Team Program (KQTD20180413181834876); Innovation and Technology Commission of the government of Hong Kong SAR (MRP/001/18X); Strategic Priority Research Program of Chinese Academy of Sciences (XDB25000000).