4332
Residual Non-local Attention Graph Learning (PNAGL) Neural Networks for Accelerating 4D-MRI1School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China
Synopsis
Residual non-local attention graph learning neural networks are proposed for accelerating 4D-MRI. Stack-of-star GRE radial sequence with self-navigator is used to acquire the data. We explore non-local self-similarity features in 4d-MR images by using residual non-local attention methods, and we use a graph convolutional network with an adaptive number of neighbor nodes to explore graph edge features. A global residual connection of graph learning model is used to further improve the performance. Through exploring non-local prior, the proposed method has the potential to be used in clinical applications such as MRI-guided real-time surgery.
Introduction
4D-MRI has the potential to be used in clinical applications, such as MR-guided surgery, and has shown clinical values in motion-corrected reconstruction in PET-MR1. However, there are some limitations of 4D-MRI, including intrinsically slow data acquisition and long reconstruction time. With the development of compressed sensing (CS) theory2, several methods have been used for MRI acceleration3-5. However, CS-based methods are computationally expensive. With the recent development of deep learning methods, several deep neural networks6-8 have demonstrated great potential to improve reconstruction quality and reduce reconstruction time. However, most deep learning methods are restricted by local convolutional operation and equal treatment of spatial and temporal elements. Graph-convolutional networks9 have been proposed to learn non-local self-similarity. In this study, we propose Residual Non-local Attention Graph Learning (PNAGL) neural networks for 4D-MRI reconstruction. We explore non-local self-similarity features in 4D-MR images by using residual non-local attention methods10. Patch-wise graph-convolution network with an adaptive number of neighbor nodes is used to further improve the performance. Through exploring non-local prior, our proposed method can achieve superior reconstruction quality compared to several state-of-the-art reconstruction methods.Theory
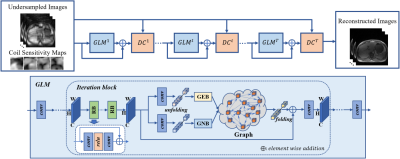
Non-local attention learns the correlations in the whole feature map, the PNAGL neural network learns the self-similarity among structures in the 4D-MR images using residual non-local attention. However, most existing non-local methods assign a fixed number of neighbors. In this study, we use a patch-wise graph-convolution network with an adaptive number of neighbor nodes to balance over-smooth and artifacts in 4D-MRI. The flowchart of the PNAGL neural network is illustrated in Figure 1, which is composed of several iterations of graph learning model (GLM) blocks and data consistency (DC) blocks. the input of the initial iteration is composed of under-sampled k-space data and sensitivity maps. The graph learning model is mainly composed of residual blocks (RB) and graph convolutional blocks. Residual blocks are used for extracting non-local features. Graph convolutional blocks are composed of graph edge blocks (GEB) and graph node blocks (GNB). Feature maps are unfolded into feature patches, different feature patches are represented as different graph nodes. Graph edge features show the connection between graph nodes, and we use a graph convolutional network with an adaptive number of neighbor nodes to explore graph edge features. A global residual connection of GLM blocks is used to further improve the performance. The data consistency blocks maintain consistency with the measured k-space data to ensure the stability of training results.Methods
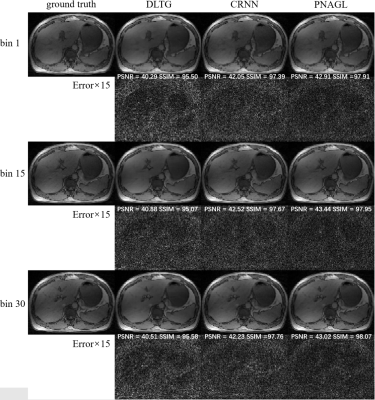
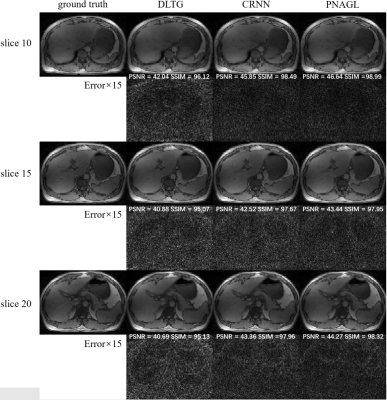
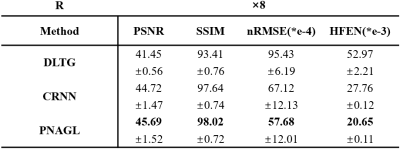
Eight healthy subjects (males, age 25.1 ± 0.6 years) were scanned on a 3 Tesla MRI scanner (uMR790; United Imaging Healthcare, Shanghai, China) with body array coil and spine coil. The acquisition method used the golden angle stack-of-stars radial GRE sequence. Each subject signed a consent form before the scan. The scan parameters for a 40-slice axial slab were FOV = 330 × 330 mm2, TR = 3.1 ms, TE = 1.49 ms, flip angle = 10°, and slice thickness = 5 mm. The number of sampling points in each spoke was 512, and the image size was 256 × 256. Each slice contained 1600 spokes. The total scanning time was 198 seconds. The center of the radial k-space line was used for self-navigation. The ground truth images were reconstructed using the XD-GRASP method. Abdominal images were reconstructed at an acceleration rate R=8. The total training data sets included 1200 = 30 × 5 × 8 (slice-motion-subject) samples, and the size of each sample was 256 × 256 × 30 (width-height-bin). The performance of the proposed method was compared to several state-of-the-art reconstruction methods with DLTG11and CRNN6.Results and Discussion
Figure 1 presents the reconstruction images in different frames of a slice with DLTG and CRNN methods at R=8 in the test datasets, Figure 2 shows the reconstruction images of different slices with other methods. The means and standard deviations of the reconstruction metrics (PSNR/SSIM/nRMSE/HFEN) are summarized in Table 1. The performance of the proposed network is improved compared with DLTG and CRNN. Compared to other deep learning based reconstruction methods, PNAGL explores the non-local self-similarity features of the whole feature patches by the graph-convolution network. Graph learning is used for 4D-MRI reconstruction for the first time, and we also introduce the residual non-local attention mechanism to explore non-local self-similarity features in 4D-MR images. Further improvement in the reconstruction quality can be expected by using a larger dataset for training.Conclusion
In this study, we propose residual non-local attention graph learning neural networks for accelerating 4D-MRI. Unlike previous local convolutional operation reconstruction methods, our network explores non-local prior information in the whole feature patches using the graph-convolution network. This proposed method has demonstrated improved reconstruction performance compared to several state-of-the-art methods. The proposed method has the potential to be used in clinical applications such as MR guided radiation therapy.Acknowledgements
This study is supported by the National Key Research and Development Program (2016YFC0103905) and the National Natural Science Foundation of China (81627901).References
1. Kustner T, Schwartz M, Martirosian P, et al. MR-based respiratory and cardiac motion correction for PET imaging. Med Image Anal. 2017;42:129-144.
2. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182-95.
3. Otazo R, Kim D, Axel L, Sodickson DK. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn Reson Med. 2010;64(3):767-76.
4. Lingala SG, Jacob M. Blind compressive sensing dynamic MRI. IEEE Trans Med Imaging. 2013;32(6):1132-45.
5. Otazo R, Candes E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn Reson Med. 2015;73(3):1125-36.
6. Qin C, Schlemper J, Caballero J, Price AN, Hajnal JV, Rueckert D. Convolutional Recurrent Neural Networks for Dynamic MR Image Reconstruction. Ieee T Med Imaging. 2019;38(1):280-290.
7. Aggarwal HK, Mani MP, Jacob M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Trans Med Imaging. 2019;38(2):394-405.
8. Zhang Y, She H, Du YP. Dynamic MRI of the abdomen using parallel non-Cartesian convolutional recurrent neural networks. Magn Reson Med. 2021;86(2):964-973.
9. Valsesia D, Fracastoro G, Magli E. Deep Graph-Convolutional Image Denoising. IEEE Trans Image Process. 2020; 8226-8237
10. Zhang Y, Li K, Li K, Zhong B, Fu Y. Residual non-local attention networks for image restoration. arXiv preprint arXiv:190310082. 2019;
11. Caballero J, Price AN, Rueckert D, Hajnal JV. Dictionary learning and time sparsity for dynamic MR data reconstruction. IEEE Trans Med Imaging. 2014;33(4):979-94.
Figures