4320
Accurate parameter estimation using scan-specific unsupervised deep learning for relaxometry and MR fingerprinting1Department of Precision Instrument, Tsinghua University, Beijing, China, 2State Key Laboratory of Modern Optical Instrumentation, College of Optical Science and Engineering, Zhejiang University, Hangzhou, China, 3Harvard Medical School, Boston, MA, United States, 4Athinoula A. Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 5School of Electrical Engineering, Korea Advanced Institute of Science and Technology, Daejeon, Korea, Republic of
Synopsis
We propose an unsupervised convolutional neural network (CNN) for relaxation parameter estimation. This network incorporates signal relaxation and Bloch simulations while taking advantage of residual learning and spatial relations across neighboring voxels. Quantification accuracy and robustness to noise is shown to be significantly improved compared to standard parameter estimation methods in numerical simulations and in vivo data for multi-echo T2 and T2* mapping. The combination of the proposed network with subspace modeling and MR fingerprinting (MRF) from highly undersampled data permits high quality T1 and T2 mapping.
Introduction
Parameter estimation methods e.g. dictionary-matching (1), variable projection (Varpro) (2) and least-squares solvers estimate relaxation parameters on a voxel-by-voxel basis, but fail to exploit spatial relations between voxels, resulting in poor estimates in acquisitions with low signal differentiation or high acceleration.Prior work on deep learning based relaxation parameter quantification aimed to learn a direct mapping from contrast-weighted images to parameter maps (3–6), which required large datasets and high-quality reference parameter maps. Such pre-trained networks may fail to generalize to new protocols with different parameter settings and to the presence of out-of-distribution features e.g. pathology.
A recent unsupervised network eliminated the need for high-quality reference maps incorporating the Bloch signal model into the network’s loss function (7). This reduced the computational burden of parameter estimation in CEST, and relied on a dataset consisting of multiple subjects.
Herein, we propose an unsupervised convolutional neural network (CNN) for parameter estimation by learning a mapping from contrast-weighted images to the desired parameter maps. This is flexible enough to incorporate Bloch- as well as subspace-modeling in the loss function, and operates in a scan-specific manner by only using data from an individual subject.
Code/data: https://cloud.tsinghua.edu.cn/d/2f732b25f34a4840b90e/
Methods
In vivo data were acquired using a Siemens Prisma system with 32ch reception.T2* mapping. Multi-echo 2D gradient echo (2D-GRE) acquisition was performed on a volunteer with matrix size=224×210×58, 10 echo times (TE1=6ms, ΔTE=6ms) and TR=5s.
T2 mapping. Single-echo spin-echo acquisitions were made on a volunteer with 4 echo times (TE1= 43ms, ΔTE=24ms), matrix size=348×384×58 and TR= 7s.
Numerical simulation: To test the robustness to noise, M0 and T2 data were generated using the output of the network, which were then used to synthesize multi-echo images. Gaussian noise with variance=0.001 was added to these multi-echo data to generate noisy inputs.
MRF acquisition. A 2D FISP sequence (8) was used to acquire ground-truth MRF data. The acquisition was repeated 6-times to collect 6 interleaves to alleviate aliasing. 30 slices with 4 mm thickness at matrix size=220×220 required 6 min/interleaf. Data were reconstructed using sliding window processing (9) with window of size=6. Parameter maps from this 6-interleaf data were used as reference. The proposed reconstruction used only a single interleaf’s data.
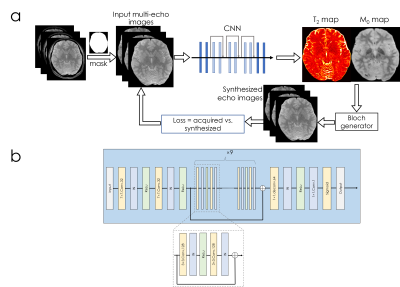
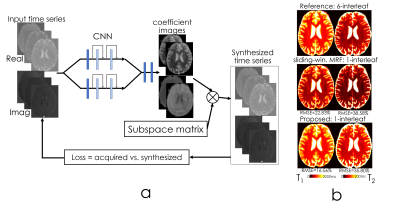
Network structure [Fig1]: A combination of convolutional, instance normalization and activation layers (ReLu) are used in the beginning, followed by nine residual blocks. SSIM loss was employed in T2 and T2* mapping, and L1 was used for MRF.
Synthesizing multi-echo data for T2 (and T2*) mapping. The output M0 and T2 maps from the network were used for synthesizing multi-echo image ⍴TE due to: $$⍴TE=M0\times\exp\left(-TE/T2\right)$$
Synthesizing time-series data for MRF. To circumvent the utilization of a non-differentiable Bloch dictionary-matching, we employed a subspace approach where the MRF dictionary was compressed to 6 coefficients (to reach 95% power in singular values). The output of the network were these coefficient maps c, which were multiplied with the subspace matrix 𝚽 (size=6×600) to obtain the synthetic MRF time-series ⍴TR due to $$⍴TR=c\times𝚽$$
Results
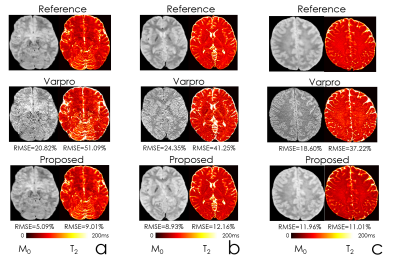
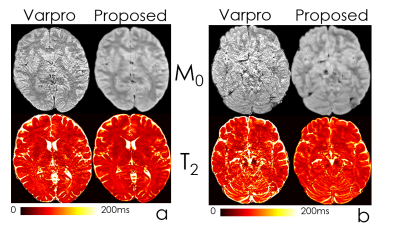
Fig2 shows the estimated parameter maps after adding Gaussian noise to the input echoes. Proposed unsupervised network was able to obtain 6-fold lower RMSE than the conventional method, Varpro.Fig3 compares the performance of Varpro and the proposed network for in vivo T2 mapping. Network’s output retains more high-frequency features, e.g. in the cerebellum, and noise amplification is largely mitigated.
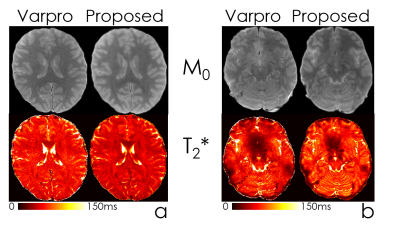
Fig4 compares the performance of Varpro and the network to estimate T2* maps, with similarly improved SNR and visualization of fine scale detail, especially in the lower slices with poor B0 inhomogeneity.
Fig5 shows the CNN structure for MRF subspace coefficient estimation. On the right, we compared T1 and T2 maps synthesized by coefficient images and standard sliding-window reconstruction using the same 1-interleaf data, and compared with the 6-interleaf acquisition. Up to 1.4-fold RMSE improvement was obtained.
Discussion
The proposed scan-specific network can leverage similarities across voxels during parameter estimation, and provides improved accuracy and robustness to noise than voxel-by-voxel estimation techniques. Incorporating Bloch modeling into the loss function allowed us to use deep learning libraries’ automatic differentiation ability, which would lend itself to additional nonlinear models e.g. free-water mapping (10).For MRF, we utilized a subspace approach to linearize the Bloch model while retaining high signal representation accuracy. This facilitated the optimization, and bypassed non-differentiable operators in dictionary-matching. Combining subspace modeling (11) with an unsupervised network allowed us to take advantage of temporal and spatial priors simultaneously.
A limitation is the training time (~12 hours/dataset). This can be improved using fine-tuning by pre-training the model, and rapidly refining in a few epochs on each individual subject’s data.
Conclusion
We demonstrated the ability of the proposed scan-specific, unsupervised network to improve the quantitative estimation accuracy over standard approaches. While using convolutional layers allowed for capitalizing on spatial relations between voxels during parameter estimation, utilizing a subspace approach for MRF facilitated the optimization with a differentiable loss function.Acknowledgements
No acknowledgement found.References
1. Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature 2013;495:187–192 doi: 10.1038/nature11971.
2. Haldar JP, Anderson J, Sun SW. Maximum likelihood estimation of T1 relaxation parameters using VARPRO. In: Proceedings of the 15th Annual Meeting of ISMRM, Berlin, Germany. ; 2007. p. 41.
3. Golkov V, Dosovitskiy A, Sperl JI, et al. q-Space Deep Learning: Twelve-Fold Shorter and Model-Free Diffusion MRI Scans. IEEE Trans. Med. Imaging 2016;35:1344–1351.
4. Aliotta E, Nourzadeh H, Patel SH. Extracting diffusion tensor fractional anisotropy and mean diffusivity from 3-direction DWI scans using deep learning. Magn. Reson. Med. 2021;85:845–854.
5. Sveinsson B, Chaudhari AS, Zhu B, et al. Synthesizing Quantitative T2 Maps in Right Lateral Knee Femoral Condyles from Multicontrast Anatomic Data with a Conditional Generative Adversarial Network. Radiology: Artificial Intelligence 2021;3:e200122 doi: 10.1148/ryai.2021200122.
6. Qiu S, Chen Y, Ma S, et al. Multiparametric mapping in the brain from conventional contrast-weighted images using deep learning. Magn. Reson. Med. 2021 doi: 10.1002/mrm.28962.
7. Kang B, Kim B, Schär M, Park H, Heo H-Y. Unsupervised learning for magnetization transfer contrast MR fingerprinting: Application to CEST and nuclear Overhauser enhancement imaging. Magn. Reson. Med. 2021;85:2040–2054.
8. Jiang Y, Ma D, Seiberlich N, Gulani V, Griswold MA. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magn. Reson. Med. 2015;74:1621–1631.
9. Cao X, Liao C, Wang Z, et al. Robust sliding-window reconstruction for Accelerating the acquisition of MR fingerprinting. Magnetic Resonance in Medicine 2017;78:1579–1588 doi: 10.1002/mrm.26521.
10. Pasternak O, Sochen N, Gur Y, Intrator N, Assaf Y. Free water elimination and mapping from diffusion MRI. Magn. Reson. Med. 2009;62:717–730.
11. Zhao B, Setsompop K, Adalsteinsson E, et al. Improved magnetic resonance fingerprinting reconstruction with low-rank and subspace modeling. Magn. Reson. Med. 2018;79:933–942.
Figures