4313

Calibrationless Reconstruction of Uniformly Undersampled Multi-channel MR data with Deep learning Estimation of ESPIRiT Maps
Junhao Zhang1,2, Zheyuan Yi1,2, Yujiao Zhao1,2, Linfang Xiao1,2, Jiahao Hu1,2, Christopher Man1,2, Yujiao Zhao3, and Ed X. Wu1,2
1Laboratory of Biomedical Imaging and Signal Processing, The University of Hong Kong, Hong Kong, China, 2Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong, China, 3The University of HongKong, HongKong, China

Synopsis

Conventional ESPIRiT reconstruction requires accurate estimation of ESPIRiT maps from autocalibration samples or signals but acquiring such autocalibration signals takes time and may not be straightforward in some situations. This study aims to deploy deep learning to directly estimate ESPIRiT maps from uniformly undersampled multi-channel 2D MR data that contain no autocalibration signals. Results show that the estimated ESPIRiT maps could be reliably obtained and they could be used for ESPIRiT and SENSE reconstruction with high acceleration.

Introduction

Conventional parallel imaging technique requires the explicit knowledge of coil sensitivities[3] or corresponding relations in k-space from either calibration scans or autocalibration signals (ACS) for reconstruction. These methods suffer from subject’s motion and additional imaging time. ESPIRiT[1], one of parallel imaging techniques in practice, could reconstruct the images from undersampled MR data through estimated ESPIRiT maps (EMS). However, the accurate estimation of ESPIRiT maps of dominant eigen values requires additional autocalibration signals[2], which takes time and may not be straightforward in some situations. The EMS are coil-dependent and each subject has slightly different coil-subject geometry in MR receiving coil system, leading to small variations in EMS. It is necessary to minimize such variations by spatial alignment and then exploit the data correlations from the same MR receiving coil system. This study aims to estimate the ESPIRiT maps directly from uniformly undersampled multi-channel 2D MR data through a 2D convolutional neural network with the U-Net architecture and apply the maps for ESPIRiT image reconstruction.

Theory and Method

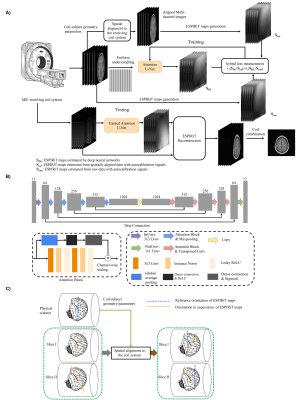
Proposed framework
EMS explicitly characterizes coil sensitivity function of MR receiving system using autocalibration signals and apply to reconstruct undersampled data in image space. EMS are coil-dependent information and different subjects may have different coil-subject geometry. This inevitably brings variations in shareable EMS among different subjects. Therefore, there is necessity to incorporate coil-subject geometry parameters to carry out spatial alignment to minimize the variations of EMS among different subjects. The framework of the proposed method is summarized in Figure 1A.
Experiment Preparation
Multi-channel coil data used in this study comes from Calgary-Campinas Public Database[4], including fully sampled human brain datasets from 67 healthy subjects collected on a 1.5T clinical scanner (GE Healthcare, Waukesha, WI). T1-weighted (T1W) acquisition parameter was TE/TR/TI = 6.3/2.6/650 ms or TE/TR/TI = 7.4/3.1/400 ms. The datasets were reduced to 6 channels by coil combination[5]. The matrix size of each channel is Nx×Ny×Nz = 128×128×100. Two parts of complex data were treated as two channels. All the data were randomly partitioned into a training/validation/test set. The multi-channel MR data are spatially aligned by performing a rigid-body rotation and translation to minimize the coil sensitivity variations. The details of data alignment were demonstrated in Figure 1C. 24 fully sampled central k-space lines were used to estimate reference ESPIRiT maps. The kernel size was set to 6×6. The k-space data were uniformly undersampled at different acceleration factors (Rs=2, 3 and 4). The model used is modified from typical U-Net[6] and attention module was introduced to effectively combine information from different channels[7].

Results

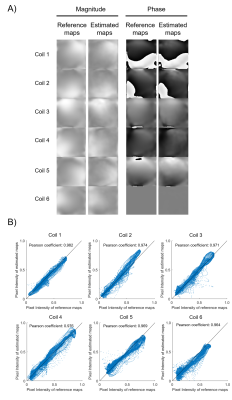
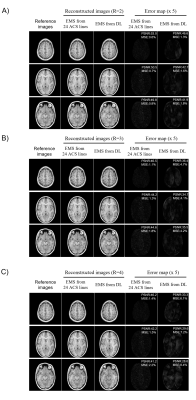
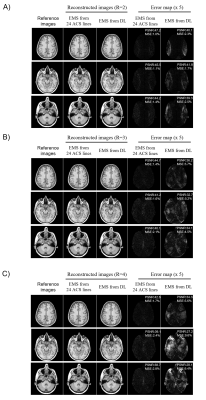
As shown in Figure 2A, EMS estimated from uniformly undersampled data (R = 4) via deep learning were comparable to reference EMS derived from 24 ACS lines and the correlation analysis also demonstrated that the estimated EMS are in good agreement with the reference EMS (shown in Figure 2B). Under the acceleration factor R=2, 3 and 4, the estimated EMS were used for ESPIRiT image-space reconstruction and the reconstructed images showed slight residual errors without pronounced artifacts compared with fully-sampled reference. Images reconstructed using estimated EMS were almost comparable to the images reconstructed using EMS from 24 ACS lines. The PSNR and MSE of reconstructed images using EMS estimated by deep learning or EMS from 24 ACS lines got worse with acceleration factor increasing from 2 to 4 as shown in Figure 3. Additionally, the estimated EMS were used for SENSE image space reconstruction and similar results as ESPIRiT reconstruction were observed as shown in Figure 4. In Figure 5, the reconstructed images with large head rotation in MR coil receiving system were shown.

Discussion and Conclusions

Without autocalibration signals, the EMS could be directly estimated from uniformly undersampled MR data by deep learning and applied to ESPIRiT/SENSE image reconstruction. The estimated EMS show high correlations to the reference EMS from 24 ACS lines. Images reconstructed using EMS based on ESPIRiT and SENSE reconstruction at high acceleration did not show apparent artifacts.
The EMS are coil-dependent and each subject has different coil-subject geometry, resulting in variation in the coil-specific EMS. Thus, we exploit the coil-subject geometry information to minimize the variations in ESPIRiT maps. Such prior information is conventionally neglected. Phase variations would also exist in scans among different subjects. Such phase changes were well preserved to some extent in our deep learning model by using a hybrid loss, one was related to minimizing the variations in coil-specific ESPIRiT sensitivity maps and another was related to preserve the phase variations.
ESPIRiT maps of dominant eigen values are estimated and used for MR image reconstruction. ESPIRiT maps corresponding to smaller eigen values can also be estimated and employed for MR image reconstruction in future study, which may further improve the image reconstruction performance, especially for ultra-high-field MRI with rapid phase variations.

Acknowledgements

This work was supported in part by Hong Kong Research Grant Council (R7003-19F, HKU17112120 and HKU17127121 to E.X.W., and HKU17103819, HKU17104020 and HKU17127021 to A.T.L.L.), Lam Woo Foundation, and Guangdong Key Technologies for Treatment of Brain Disorders (2018B030332001) to E.X.W..

References

[1] Uecker, M., et al., ESPIRiT-An Eigenvalue Approach to Autocalibrating Parallel MRI: Where SENSE Meets GRAPPA. Magnetic Resonance in Medicine, 2014. 71(3): p. 990-1001.

[2] Sodickson, D., Parallel magnetic resonance imaging (or, scanners, cell phones, and the surprising guises of modern tomography). Medical Physics, 2007. 34(6): p. 2598-2598.

[3] Pruessmann, K.P., et al., SENSE: Sensitivity encoding for fast MRI. Magnetic Resonance in Medicine, 1999. 42(5): p. 952-962.

[4] Warfield, S.K., K.H. Zou, and W.M. Wells, Simultaneous truth and performance level estimation (STAPLE): An algorithm for the validation of image segmentation. Ieee Transactions on Medical Imaging, 2004. 23(7): p. 903-921.

[5]Buehrer, M., et al., Array compression for MRI with large coil arrays. Magnetic Resonance in Medicine, 2007. 57(6): p. 1131-1139.

[6] Ronneberger, O., P. Fischer, and T. Brox, U-Net: Convolutional Networks for Biomedical Image Segmentation. Medical Image Computing and Computer-Assisted Intervention, Pt Iii, 2015. 9351: p. 234-241.

[7] Hu, J., L. Shen, and G. Sun, Squeeze-and-Excitation Networks. 2018 Ieee/Cvf Conference on Computer Vision and Pattern Recognition (Cvpr), 2018: p. 7132-7141.

Figures

Figure 1. The pipeline of the study and the involved architecture of the model and data spatial alignment. A. The pipeline of ESPIRiT maps (EMS) estimation and ESPIRiT/SENSE reconstruction. B. The architecture of the Attention U-Net. C. The illustration of data spatial alignment.

Figure 2. Comparison of the estimated ESPIRiT maps with the reference ESPIRiT maps (R=4, Coil=6). A. The magnitude and phase of reference maps (from fully sampled data) and deep learning estimated maps (from undersampled data). The phase difference maps (from channel 6) are normalized to [-pi, pi] B. The correlations between estimated and reference magnitude maps.

Figure 3. Comparison of ESPIRiT reconstructed images using estimated ESPIRiT maps (EMS) from 24 ACS lines and deep learning (R=2, 3, and 4; 6-channel coil). PSNR: peak signal to noise ratio. MSE: mean squared error.

Figure 4. Comparison of SENSE reconstructed images using estimated ESPIRiT maps (EMS) from 24 ACS lines and deep learning (R=2, 3, and 4; 6-channel coil). PSNR: peak signal to noise ratio. MSE: mean squared error.

Figure 5. Results of ESPIRiT reconstructed images from two subjects with the largest head rotations (top and bottom two rows, respectively) using estimated ESPIRiT maps (EMS) from 24 ACS lines and deep learning (R=4; 6-channel coil). PSNR: peak signal-to-noise ratio. MSE: mean squared error.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
4313
DOI: https://doi.org/10.58530/2022/4313