4186
Dynamic MRI Reconstruction of the Whole Liver with High Acceleration using Low Rank Tensor and Weighted Group Sparsity1School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China
Synopsis
We propose an algorithm for dMRI reconstruction from highly under-sampled k-space data acquired during free breathing. Stack-of-star GRE radial sequence with self-navigator is used to acquire the data. We explore spatial and temporal redundancy for the reconstruction by using weighted group sparsity, weighted sparsity, and low-rank tensor. Additionally, a tensor total variation is used to ensure spatial and temporal smoothness. By applying a weighting function to the sparsity and group sparsity, the subtle structural sparsity features in the sparse domain can be better utilized. The proposed algorithm has the potential to be used in clinical applications such as MR-guided surgery.
Introduction
Dynamic Magnetic Resonance Imaging (dMRI) of the liver during free-breathing has potential applications in MRI-guided radiotherapy and motion-corrected reconstruction in PET-MR. However, dMRI is limited by intrinsically slow data acquisition. It is desirable to improve reconstruction quality from highly under-sampled k-space data. Compressed sensing (CS)1,2 based algorithms have been used for accelerated reconstruction. Previous studies use low rank constraints or combine rank deficiency and transform domain sparsity3-5 to achieve superior performance. in this study, we propose a Low Rank plus Weighted Group Sparse Tensor decomposition (LRWGST) algorithm for dMRI reconstruction without the need for reference images. We explore spatial and temporal redundancy by using the low rank, weighted group sparsity, and weighted sparsity. Additionally, a tensor total variation is used to ensure spatial and temporal smoothness. Through exploring prior information in the data, the proposed algorithm can achieve superior reconstruction quality compared to several state-of-the-art reconstruction algorithms in dMRI of the whole liver.Theory
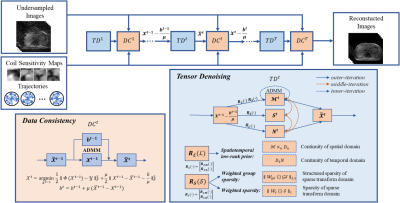
Weighted group sparsity6 is an extension to sparse representation and explores similar information in different groups of data. The low rank and sparsity explore both spatial and temporal prior information in dMRI. We combine the weighted group sparsity and low-rank tensor decomposition into the reconstruction framework, and the proposed LRWGST can be expressed as: $$\min _{\mathcal{M}, N, \mathcal{S}, \mathcal{X}} \|\boldsymbol{\Phi}(\mathcal{X})-\mathcal{Y}\|_{F}^{2}+\alpha\left\|\mathcal{X}-\mathcal{M} \times{ }_{3} N-\mathcal{S}\right\|_{F}^{2}+\beta\left\|D_{3} N\right\|_{F}^{2}+\gamma\left\|\mathcal{W}_{n} \odot\left(\mathcal{M} \times_{n} D_{n}\right)\right\|_{2,1}+\lambda\left\|\mathcal{W}_{s} \odot \mathcal{S}\right\|_{1}$$ where $$$\mathcal{Y}$$$ represents acquired k-space data, $$$\mathcal{X}$$$ is the desired image series, $$$\boldsymbol{\Phi}$$$ is the NUFFT operator. $$$\mathcal{M}$$$ represents the spatial prior factor, $$$N$$$ denotes temporal prior factor, $$$\mathcal{S}$$$ represent sparse prior. $$$D_{n} (n = 1,2)$$$ and $$$D_{3}$$$ are first-order difference matrices along different dimensions, $$$\mathcal{W}_{n} (n = 1,2)$$$ and $$$\mathcal{W}_{s}$$$ are weighted tensors of the weighted group sparsity term and the weighted sparsity term respectively. $$$\alpha, \beta, \gamma, \lambda$$$ are regularization parameters. The flowchart of LRWGST algorithm is illustrated in Figure 1. The reconstruction based on LRWGST can be split into two sub‐problems by the ADMM algorithm: the data consistency step and tensor denoising step using low-rank plus weighted group sparse regularized constraints. The data fidelity term maintains consistency with the measured non-Cartesian k-space data, and the tensor denoising term is solved by proximal alternating minimization algorithm alternately through three iterative steps: the $$$\mathcal{M}^{t}$$$-step, $$$N^{t}$$$-step and $$$\mathcal{S}^{t}$$$-step.Methods
Eight healthy subjects (males, age 25.1±0.6 years) were scanned on a 3T MRI scanner (uMR790; United Imaging Healthcare, Shanghai, China). A golden angle stack-of-stars GRE radial sequence was used for acquisition. Each subject signed a consent form before the scan. The scan parameters for a 40-slice axial slab were FOV=330×330mm2, TR=3.1ms, TE=1.49ms, flip angle=10°, and slice thickness=5mm. The number of sampling points in each spoke was 512, and the image size was 256×256. Each slice contained 1600 spokes. The total scanning time was 198 seconds. The center of the radial k-space line was used for self-navigation. The ground truth images were reconstructed by the XD-GRASP algorithm. Abdominal images were reconstructed at different acceleration rates R=4/8/16/25. Abdominal dynamic contrast-enhanced (DCE) MRI data were obtained from a public dataset5. The imaging parameters of the DCE dataset include: 12-element receiver coil, FOV=380×380mm2, image size of 384×384, the number of sampling points in each spoke was 384. The performance of the proposed algorithm was compared to that of the state-of-the-art reconstruction algorithms with L+S5, BCS4, SRTPCA7, PROST8,9, and deep learning algorithm with 3D-CNN, and PNCRNN10,11.Results
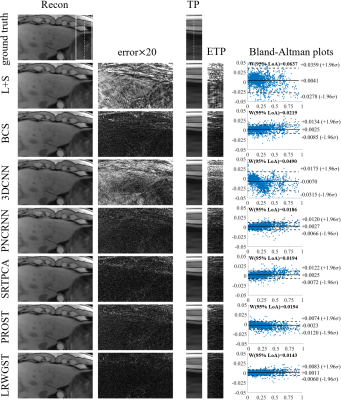
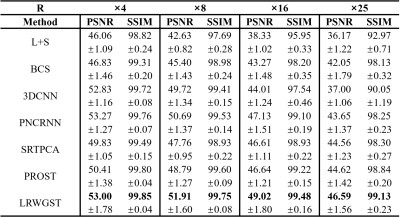
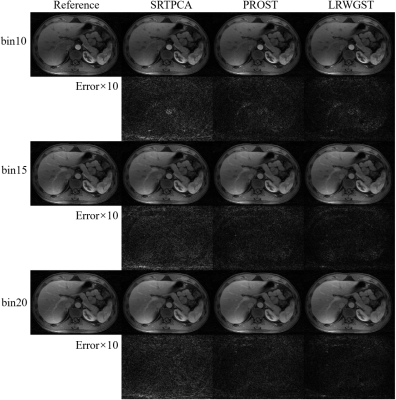
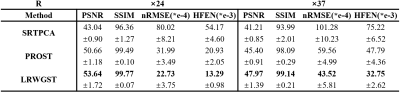
The means and standard deviations of the reconstruction metrics (PSNR/SSIM) across 8 subjects are summarized in Table 1. The comparison shows that LRWGST improves the reconstruction quality compared to L+S, BCS, 3D-CNN, PNCRNN, SRTPCA, and PROST. The performance of LRWGST is substantially improved compared with other algorithms, especially at high acceleration factors. Figure 2 presents the difference between the reconstructions and the ground truth images with the Bland-Altman plots at R=25 in a typical subject. The spatial structures and the temporal profiles are more accurately reconstructed with LRWGST. The Bland-Altman analysis shows that LRWGST results in the narrowest width of 95% limits of agreement. Figure 3 presents the comparison of images reconstructed with different algorithms with the ground truth images at R=37 in the DCE data. The means and standard deviations of the reconstruction metrics (PSNR/SSIM/nRMSE/HFEN) in the DCE data are summarized in Table 2. The comparison shows that LRWGST achieves superior performance compared to SRTPCA and PROST.Discussion and Conclusion
We present an algorithm to utilize weighted group sparsity, weighted sparsity, tensor total variation, and low-rank tensor for the reconstruction of dMRI of the whole liver from highly under-sampled k-space data acquired during free breathing. By using group sparsity, the structural features in the sparse domain can be better preserved. By applying a weighting function to the sparsity and group sparsity, the subtle structural sparsity features in the sparse domain can be better utilized. The proposed algorithm does not require reference images. As such, this algorithm can be used in scenarios when fully sampled reference images are not available. The results demonstrate that the proposed algorithm can achieve superior reconstruction quality compared to several state-of-the-art reconstruction algorithms especially at R=16 and 25. The proposed algorithm has the potential to be used in clinical applications such as MR-guided surgery.Acknowledgements
This study is supported by the National Key Research and Development Program (2016YFC0103905) and the National Natural Science Foundation of China (81627901).References
1. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182-95.
2. Donoho DL. Compressed sensing. IEEE Transactions on information theory. 2006;52(4):1289-1306. 3. Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated dynamic MRI exploiting sparsity and low-rank structure: k-t SLR. IEEE Trans Med Imaging. 2011;30(5):1042-54.
4. Lingala SG, Jacob M. Blind compressive sensing dynamic MRI. IEEE Trans Med Imaging. 2013;32(6):1132-45.
5. Otazo R, Candes E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn Reson Med. 2015;73(3):1125-36.
6. Tang X, Feng G, Cai J. Weighted group sparse representation for undersampled face recognition. Neurocomputing. 2014;145:402-415.
7. Liu Y, Liu T, Liu J, Zhu C. Smooth robust tensor principal component analysis for compressed sensing of dynamic MRI. Pattern Recognition. 2020;102
8. Bustin A, Voilliot D, Menini A, et al. Isotropic Reconstruction of MR Images Using 3D Patch-Based Self-Similarity Learning. IEEE Trans Med Imaging. 2018;37(8):1932-1942.
9. Bustin A, Lima da Cruz G, Jaubert O, Lopez K, Botnar RM, Prieto C. High-dimensionality undersampled patch-based reconstruction (HD-PROST) for accelerated multi-contrast MRI. Magn Reson Med. 2019;81(6):3705-3719.
10. Qin C, Schlemper J, Caballero J, Price AN, Hajnal JV, Rueckert D. Convolutional Recurrent Neural Networks for Dynamic MR Image Reconstruction. Ieee T Med Imaging. 2019;38(1):280-290.
11. Zhang Y, She H, Du YP. Dynamic MRI of the abdomen using parallel non-Cartesian convolutional recurrent neural networks. Magn Reson Med. 2021;86(2):964-973.
Figures