Introduction

Traditional cardiac CINE MR imaging provides an averaged heart beat movie by segmenting the acquisition, and is sensitive to patient arrhythmia and incomplete breath-control. Real-time dynamic imaging techniques based on low rank matrix decomposition can provide continuous cardiac images under free-running conditions^[1]. However, these techniques suffer from long reconstruction time (usually >10min)^[2,3]. Deep-learning based techniques lack ground-truth images for training in this scene, and the need for GPU resources also limits their application in clinical practice. In this work, we proposed an improved real-time cardiac imaging technique, which keeps the merits of high temporal resolution (~10ms), free-running without ECG or breath-control, continuous frames without averaging, and achieves an ultra-fast reconstruction speed. The whole process of acquisition and reconstruction can be finished in only 1 minute.

Methods

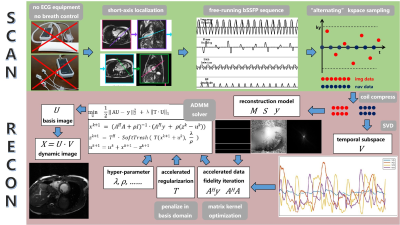
Imaging Model
We use the regularized partial separable model^[3] as the basic imaging model:
$$ \min_U{\frac{1}{2}\left \| M\odot FS(VU) -y \right \|_2^2 +R(U) } $$
where the symbols represent: spatial subspace U, temporal subspace V, coil sensitivity maps S, Fourier transform F, under-sampling mask M, and acquired k-space data y. $$$\odot$$$ denotes element-wise multiplication.

Intuition
In previous work, the regularization term $$$ R(\cdot ) $$$ usually forces some kind of sparsity (transform T) in dynamic image domain:
$$ R(U)=\left \| T(VU) \right \| _1 $$
Optimization of this term usually requires iterative soft-thresholding of thousands of time frames, which is computational expensive. Thus, we seek to find a constraint which directly penalize in some domain which has the same size of U, while also provides a good regularization effect.

Regularization Term
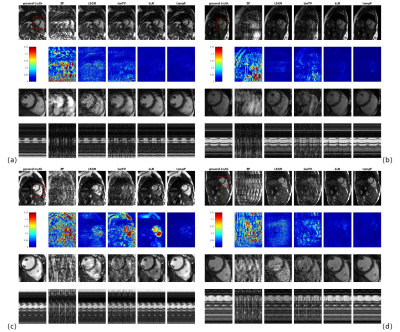
We test 3 constraints in this work: isotropic total variation (isoTV)^[4], local low rank (LLR)^[5], and the Frobenius norm of temporal difference (tempF):
$$ isoTV(U)=\sum_{i,j} \sqrt{\left | (D_{x}\cdot U)_{i,j} \right |^2 + \left | (D_{y}\cdot U)_{i,j} \right |^2} $$
$$ LLR(U)= \sum_{i} \left \| T_{LLR}(U)_{i} \right \|_{*} $$
$$ tempF(U)=\frac{1}{2} \left \| \Phi \cdot VU \right \|_{F}^2 $$
where $$$D_{x}$$$ and $$$D_{y}$$$ denotes first order difference operator^[4], $$$T_{LLR}$$$ denotes the patch extraction operator^[5], $$$\Phi$$$ denotes temporal first order difference matrix.

Data Consistency Term
The optimization of data consistency term relies on the gradient:
$$ \frac{\partial }{\partial U} \left ( \frac{1}{2}\left \| M\odot FS(VU) -y \right \|_2^2 \right )= V^HS^HF^HM\odot FS VU-V^HS^HF^Hy $$
It can be proved that the operator position between V and S, V and F can be exchanged^[6], giving:
$$ S^HF^H(V^HM\odot V)FSU-V^HS^HF^Hy $$
It can be further proved that the operator $$$V^HM\odot V$$$ can be substituted by a matrix kernel^[7], which totally remove time dimension in the expression.

The overall pipeline from data acquisition to image reconstruction is shown in Figure 1.

Retrospective Experiment
We use the online OCMR cardiac CINE k-space dataset^[8] for retrospective undersampling and simulate the real-time scan and reconstruction. A total of 49 slices of short axis CINE images is selected from 17 subjects.

Prospective Experiment
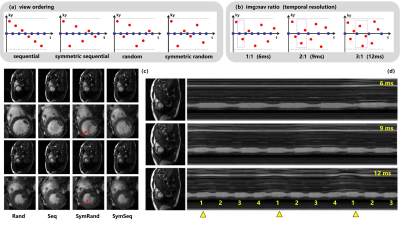
Realtime free-running cardiac imaging sequence was implemented on a 3T clinical scanner (Philips IngeniaCX R5.7.1; Best, Netherlands). To optimize the technique, three different img:nav ratios and four different phasing encoding view order settings are tested.
The final optimized realtime free-running cardiac imaging technique is compared to clinical CINE sequence on the scanner under quite similar scan parameters:FOV = 300mm x 300mm, voxel size = 2mm x 2mm, matrix size = 152 x 150, slice thickness = 8mm, flip angle = 45 degree, TR$$$\approx $$$3ms, TE$$$\approx $$$1.5ms
The cardiac phases of CINE imaging is 22, equivalent to temporal resolution of 45 ms, which requires a total acquisition time of 11s.The acquisition time of realtime cardiac imaging is 30s, which produces 2250 time frames.

Experiments and Results

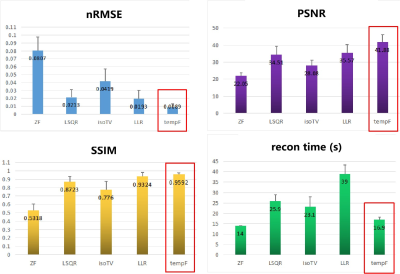
Retrospective Experiment
The result is shown in Figure 2. In addition to the three constrained reconstruction algorithms listed above, zero-filling and least-square reconstruction are also implemented for comparison. The quantitative comparison is given in Figure 3. It is demonstrated that tempF produce the best performance and is used for the following prospective experiments.

Prospective Experiment
The comparative result is given in Figure 4. As a conclusion, random view order is demonstrated to produce the best image quality. And img:nav = 3:1 is prefered because total acquisition time is reduced due to less nav acquisition.
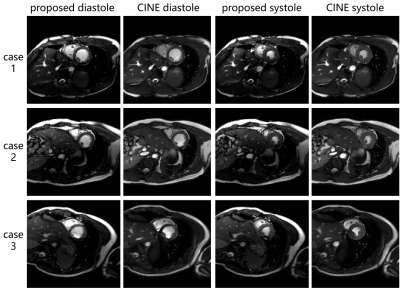
As shown in Figure 5, the proposed technique produces comparable image quality with clinical standard CINE images, and achieves 12ms temporal resolution, free-running without ECG or breath-control, and displays a continuous movie of the heart during the whole acquisition period. Most significantly, the acquisition and reconstruction can be finished within just 1 minute.

Discussion and Conclusion

The main contribution of this work is successfully reducing the reconstruction time of realtime cardiac imaging to a clinically acceptable level. We noticed that a significant dimensionality reduction is achieved by modeling dynamic images as low-rank (such as partial separable model). This should not only help with recovering signal from undersampled observations, but also help to reduce the computational cost. By elaborately designing regularization term and optimizing the implementation, the whole iterative process can be performed in the low-dimensional domain, which is the key of reducing reconstruction time.
Combining the merits of realtime free-running imaging with fast acquisition and reconstruction efficiency, this technique has great potential for the cardiac imaging for patients with arrhythmia.

Acknowledgements

Special thanks to Dr. Zhensen Chen for his help with sequence development coding.