4092
Iterative decomposition of multi-compartment relaxometry with least square estimations (IDMCR) for UTE relaxometry in brain
Jingwen Yao1, Nikhil Deveshwar1,2, and Peder E. Z. Larson1
1Department of Radiology and Biomedical Imaging, University of California, San Francisco, San Francisco, CA, United States, 2Graduate Program in Bioengineering, UCSF/UC Berkeley, San Francisco, CA, United States
1Department of Radiology and Biomedical Imaging, University of California, San Francisco, San Francisco, CA, United States, 2Graduate Program in Bioengineering, UCSF/UC Berkeley, San Francisco, CA, United States
Synopsis
To improve the fitting performance of a UTE relaxometry model, we proposed an iterative decomposition method of multi-compartment relaxometry with least square estimations (IDMCR), based on Gauss-Newton estimations and incorporating spatial constraints. Monte Carlo simulation showed that IDMCR provided robust and unbiased estimation of ultra-short T2* myelin fraction, which was further improved by adding spatial constraints. We examined the fitting algorithm in one healthy volunteer UTE relaxometry data and showed clear contrast of gray and white matter on the fitted myelin fraction map. The framework of IDMCR could also be easily adapted for other nonlinear parameter fitting problems.
Introduction
Multi-compartment relaxometry provides quantitative measurements for various in vivo applications, including myelin water imaging1 and fat quantification2. Recently, an ultra-short echo (UTE) relaxometry method was proposed to directly measure the bound protons in the myelin phospholipid membranes by fitting a two-compartment model3. Despite the great promises, the fitting of multi-compartment relaxometry is often ill-conditioned due to the large number of fitting parameters, leading to degraded stability. In this project, we proposed an iterative decomposition of multi-compartment relaxometry with least square estimations (IDMCR) incorporating spatial constraints. We evaluated the noise performance of the proposed method using numerical simulations of UTE relaxometry and tested the algorithm in a healthy volunteer.Algorithm
The proposed IDMCR method for a variable flip angle multi-echo GRE acquisition is demonstrated in Fig.1. Following the same principles of the T2*-IDEAL technique4,5, the algorithm iteratively updates the parameter estimations using Gauss-Newton steps with Taylor’s approximation. To address the ill-conditioned problem, we further incorporated spatial constraints into a second loop of iteration (constrained IDMCR). Starting from the second outer loop, the spatial constrained parameter maps are incorporated into the Gauss-Newton steps as priors in generalized Tikhonov regularization. In the example application of UTE relaxometry fitting, we fixed the chemical shift between water and myelin lipid to reduce the degree of freedom and adopted a multifrequency model of myelin lipid6 for more accurate quantification.Methods
Monte Carlo Simulation: To evaluate the accuracy and precision of the fitting algorithm, we performed numerical simulations of a two-pool signal model with an ultrashort-T2* lipid component and a long-T2* water component. The simulation parameters of tissue properties and acquisition are listed in Fig.2(A-B), including myelin proton fraction (MPF) ranging from 5% to 32%. Random complex gaussian noise was added to 1000 replications at SNR of 25/50/100/200. The simulated signals were fitted with the original IDMCR algorithm. We also performed the fitting using the lsqnonlin function in MATLAB for comparison. In addition, we simulated the same dataset with 1000 replications using random relative B1 with 10% standard deviation, to evaluate the sensitivity of the proposed method to B1 inhomogeneity.Digital Phantom Simulation: We created a 128x128 digital phantom with spatially varying frequency offset and 9 circular ROIs. The phantom signals were created with the same simulation parameters and MPF ranging from 5% to 29% at the SNR of 50. The original IDMCR was performed at each voxel independently, whereas the constrained IDMCR imposed median filtering of the field map and wavelet denoising of the myelin component relaxometry maps in the outer loop (Fig.1). The Tikhonov regularization weights were set to 0.1 for all three fitting parameters.
Healthy Volunteer Data Fitting: We scanned one healthy volunteer on a 3T GE scanner using a UTE sequence with the same acquisition parameters described in the simulation experiments. The spatially constrained IDMCR was used to fit the model parameters. The fitted MPF values in gray and white matter were extracted using brain segmentation obtained from FMRIB's Automated Segmentation Tool8.
Results
The fitted MPF obtained from Monte Carlo simulation showed accurate estimation using the proposed IDMCR algorithm, with the slopes of linear fitting between ground truth and estimated MPF close to 1 (Fig.2(C)). B1 variations between -20% and 20% induced very limited bias (Fig.2(D)). The estimated MPF introduced a positive bias at lower fractions with decreasing SNR (Fig.2(E)), although the mean bias was lower than 1% for all SNR evaluated (25-200). Similarly, the standard deviation (SD) of fitted MPF increased with decreasing SNR (Fig.2(F)). The least-square nonlinear fitting performed similarly to IDMCR in this evaluation (Fig.2(E-F)). In the digital phantom evaluation, the constrained IDMCR produced a much smoother field map compared to the original IDMCR (Fig.3(A-B)), as well as a less noisy MPF estimation (Fig.3(C-D)). The smoother fitting maps can also be appreciated from the line profiles of fitting map estimations (Fig.3(E-G)). The ROI analysis showed reduced mean fitting SD from 2.0% to 1.3% using the spatial constraints. For the in vivo data acquired at three FAs with 24 total TEs (Fig. 4(A)), we generated the MPF map using spatially constrained IDMCR (Fig.4(C)). The histogram of gray and white matter MPF values showed higher MPF in the white matter (Fig.4(D)).Discussion and Conclusion
In this study, we proposed a multi-compartment relaxometry fitting algorithm based on the iterative Gauss-Newton method. We evaluated the method in the context of two-compartment UTE relaxometry fitting using numerical simulation and in vivo experiment. The IDMCR provided unbiased MPF estimations with small variation (SD<2%) at SNR greater than 50. The fitting results were insensitive to B1 variation and were comparable to the conventional nonlinear fitting. The constrained IDMCR further improved the robustness of MPF fitting by incorporating different spatial constraints on the fitting maps. With the healthy volunteer UTE relaxometry data, we showed clear contrast of gray and white matter on the fitted MPF map. Future work includes incorporating the line search into the Gauss-Newton step for faster convergence, exploring different spatial constraints, physical phantom validation, and optimizing the Tikhonov regularization parameters. The framework of the proposed IDMCR algorithm could also be easily adapted for other nonlinear parameter fitting problems.Acknowledgements
No acknowledgement found.References
- Chan KS, Marques JP. Multi-compartment relaxometry and diffusion informed myelin water imaging - Promises and challenges of new gradient echo myelin water imaging methods. Neuroimage. 2020 Nov 1;221:117159. doi: 10.1016/j.neuroimage.2020.117159. Epub 2020 Jul 11. PMID: 32663644.
- Chebrolu VV, Hines CD, Yu H, Pineda AR, Shimakawa A, McKenzie CA, Samsonov A, Brittain JH, Reeder SB. Independent estimation of T*2 for water and fat for improved accuracy of fat quantification. Magn Reson Med. 2010 Apr;63(4):849-57. doi: 10.1002/mrm.22300. PMID: 20373385; PMCID: PMC3070176.
- Boucneau T, Cao P, Tang S, Han M, Xu D, Henry RG, Larson PEZ. In vivo characterization of brain ultrashort-T2 components. Magn Reson Med. 2018 Aug;80(2):726-735. doi: 10.1002/mrm.27037. Epub 2017 Dec 1. PMID: 29194734; PMCID: PMC5910201.
- Yu H, Shimakawa A, McKenzie CA, Brodsky E, Brittain JH, Reeder SB. Multiecho water-fat separation and simultaneous R2* estimation with multifrequency fat spectrum modeling. Magn Reson Med. 2008 Nov;60(5):1122-34. doi: 10.1002/mrm.21737. PMID: 18956464; PMCID: PMC3070175.
- Bydder M, Ghodrati V, Gao Y, Robson MD, Yang Y, Hu P. Constraints in estimating the proton density fat fraction. Magn Reson Imaging. 2020 Feb;66:1-8. doi: 10.1016/j.mri.2019.11.009. Epub 2019 Nov 15. PMID: 31740195.
- Wilhelm MJ, Ong HH, Wehrli SL, Li C, Tsai PH, Hackney DB, Wehrli FW. Direct magnetic resonance detection of myelin and prospects for quantitative imaging of myelin density. Proc Natl Acad Sci U S A. 2012 Jun 12;109(24):9605-10. doi: 10.1073/pnas.1115107109. Epub 2012 May 24. PMID: 22628562; PMCID: PMC3386098.
- Wright PJ, Mougin OE, Totman JJ, Peters AM, Brookes MJ, Coxon R, Morris PE, Clemence M, Francis ST, Bowtell RW, Gowland PA. Water proton T1 measurements in brain tissue at 7, 3, and 1.5 T using IR-EPI, IR-TSE, and MPRAGE: results and optimization. MAGMA. 2008 Mar;21(1-2):121-30. doi: 10.1007/s10334-008-0104-8. Epub 2008 Feb 8. PMID: 18259791.
- Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging. 2001 Jan;20(1):45-57. doi: 10.1109/42.906424. PMID: 11293691.
Figures
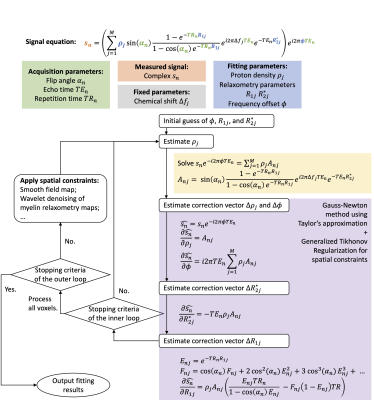
Figure 1. Schematic diagram of the iterative decomposition method of multi-compartment relaxometry with least square estimations (IDMCR) algorithm, using an example signal model from a variable flip angle multi-echo GRE acquisition.
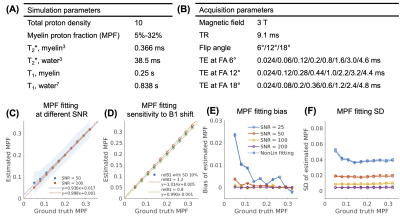
Figure 2. Monte Carlo simulation parameters and results. (A-B) Simulation parameters of tissue properties and MRI acquisition. (C) Linear correlation of estimated and ground truth myelin proton fraction (MPF), with shaded regions representing the SD of the fitting results. (D) Linear correlation of ground truth and estimated MPF at varying B1 shifts. (E-F) Bias and variation of the fitted MPF at different SNR. Dashed lines represented the conventional nonlinear fitting. MPF: myelin proton fraction; SD: standard deviation.
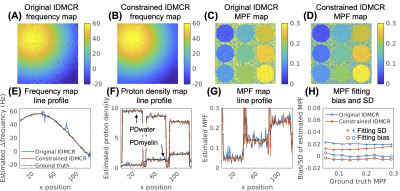
Figure 3. Comparison of IDMCR with and without spatial constraints in phantom simulation. Field map estimations (A-B) and MPF map estimations (C-D) using the original and the constrained IDMCR were demonstrated. (E-G) Line profiles of field map, proton density maps, and MPF map. (H) Comparison of MPF fitting performance. IDMCR: iterative decomposition method of multi-compartment relaxometry with least square estimations; MPF: myelin proton fraction; PD: proton density; SD: standard deviation.
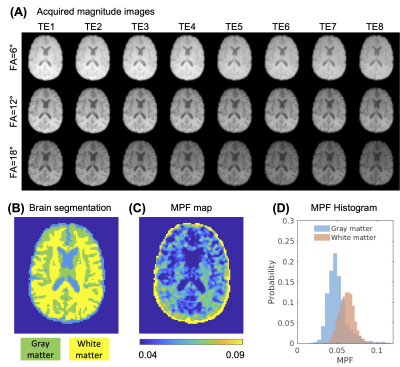
Figure 4. Healthy volunteer UTE relaxometry fitting. (A) Magnitude images of an acquired variable flip angle multi-echo UTE dataset at 3T. (B) Three-compartment brain tissue segmentation. (C) MPF map showing gray and white matter contrast. (D) The comparison of gray and white matter MPF histograms. UTE: ultrashort echo time; MPF: myelin proton fraction.
DOI: https://doi.org/10.58530/2022/4092