Introduction

Hyperpolarized gas (HPG) MRI is a technique in which high resolution images of lung function are obtained in a single breath-hold. Quantitative analysis of HPG images requires accurate segmentation of the signal within the lung boundaries. However, because HPG images are background-free, the lung boundary is not visible, and segmentation is often performed manually which is time-consuming and prone to error, especially in cases of many large ventilation defects. Here, we model the variation of lung segmentation by a probability distribution parametrized with a transferred conditional generative adversarial neural network¹. We generate confidence masks from this distribution on a slice-by-slice basis and then stack and aggregate them to obtain a 3D mask. This procedure is inspired by the behavior of a human expert. The performance is assessed on test subjects with moderate to high ventilation defect percentage (VDP 25-38%), which is the percentage of voxels with <60% of the whole-lung HP gas signal mean². We measured the performance by the Dice score between the predicted mask and the ground truth generated by the simultaneously-obtained proton images and compute the correlation of Dice score between our method and a human expert.

Methods

HPG ³He MR images were acquired in 34 asthma patients using 3D-TrueFISP (TR/TE=1.9/0.8, matrix=80x128, FA=9°, isotropic voxel dimension: 3.9mm, acquisition time=~10 s). Slice-by-slice segmentation was performed on 2D ventilation slices $$$A_i^v$$$ which outputs 2D segmentation masks, where $$$i=1,\cdots,n_v$$$ and $$$n_v$$$ is the number of slices of a given view $$$v\in$$$ {coronal, axial, sagittal}. We then stacked them into a 3D volume and aggregated the results of the three views.

Probabilistic segmentation and conditional GAN

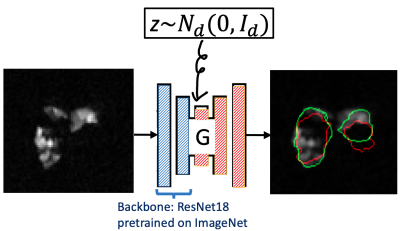
We model the segmentation uncertainty on a given ventilation slice $$$A$$$ of large defect by a conditional distribution $$$P_v(B|A)$$$, where $$$B$$$ is a candidate segmentation mask on $$$A$$$. We parameterize $$$P_v(B|A)$$$ by a U-net generator (Figure 1), which is trained by a modified conditional generative adversarial network (GAN) called BicycleGAN¹ with transfer learning. Specifically, the loss function is an equal combination between Dice and binary cross entropy loss, and the backbone of the generator is the residual network 18³ (ResNet 18) pretrained on the ImageNet. It is well known that generators trained with BicycleGAN can perform multi-modal sampling, which is crucial given the irregular shape of lungs; the transfer learning is a remedy of a small training set. For training, 2D multi-slice hyperpolarized MR images and proton-generated masks $$$(A_i^v,B_i^v)$$$ from 34 asthma patients were used (VDP=2%-40%). $$$\widehat P_v(B|A)$$$ is denoted as the learned $$$P_v(B|A)$$$. The $$$\alpha$$$-confidence mask $$$B_{v,\alpha}(A)$$$ is the mask that covers the samples generated by $$$\widehat P_v(B|A)$$$ with probability $$$\alpha$$$, i.e. $$$B_{v,\alpha}(A)$$$ satisfies $$P\left(B\in B_{v,\alpha}(A)\middle| B\sim{\widehat P}_v\left(\cdot\middle| A\right)\right)=\alpha,\ v\in\{coronal, axial, sagittal\}.\quad\quad\quad\mbox{(1)}$$ Obviously $$$B_{v,\alpha_1}(A)\subset B_{v,\alpha_2}(A)$$$ when $$$\alpha_1\leq\alpha_2$$$. As shown in Figure 2, the $$$\alpha$$$-confidence masks $$$B_{coronal,\alpha}(A)$$$ for $$$\alpha$$$ = 0.05, 0.5 and 0.95 greatly overlap with each other when $$$A$$$ has a low defect percentage ((b) of Figure 2), while differing when $$$A$$$ has a high defect percentage ((a) of Figure 2). This shows that our model captures the segmentation uncertainty caused by ventilation defects.

Three-view aggregation

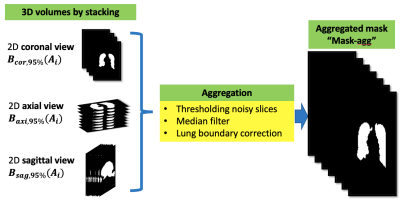
We separately obtain $$$B_{coronal,0.95}(A_{coronal}), B_{axial,0.95}(A_{axial})$$$ and $$$B_{sagittal,0.95}(A_{sagittal})$$$ by Eq. (1), where $$$ A_{coronal}$$$, $$$ A_{axial}$$$ and $$$A_{sagittal}$$$ are 2D image slices obtained from the 3D image array. Only slices with signal intensities greater than four times the mean of the HPG image set are considered. We stack the 2D segmentations, as shown in Figure 3, and aggregate the 3D segmentation of each view using a median filter (3×3 kernel to each slice). We denoted the aggregated mask as “Mask-agg”, and the mask formed by $$$B_{coronal,0.95}(A_{coronal})$$$ as “Mask-cor”.

Results

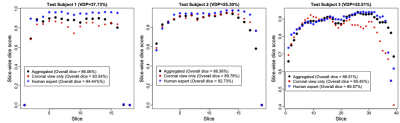
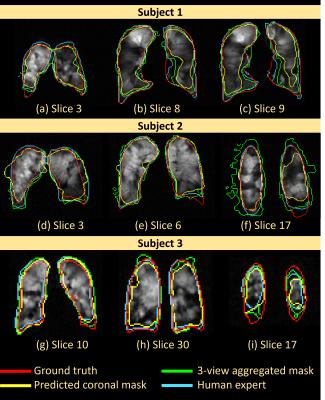
Performance is measured by $$\mbox{Dice Score (DS)} = \frac{2\ast\left|\mathrm{predicted\ mask}\ast\mathrm{ground\ truth\ mask}\right|}{\left|\mathrm{predicted\ mask}\right|+\left|\mathrm{ground\ truth\ mask}\right|}.$$In three out of five test subjects, the Mask-agg had a higher overall DS than Mask-cor. The median correlation between the slice-wise DS and the slice-wise VDP of the five test subjects was -0.7863 (P value < 0.01 for four out of five subjects). The average correlation in the slice-wise DS between human expert and Mask-agg was 0.7165. The DS of Mask-agg was lower (P value < 0.01) than that of the human expert on four of the five test subjects. For the healthy subject (VDP=2.43%), Mask-cor achieved a DS of 92.07%. Figure 4 and Figure 5 show the slice-wise DS and mask for three selected subjects and slices.

Discussion

The segmentation Mask-agg is highly correlated with but generally underperforms the human expert with exceptions of Slices (a), (d) and (i) in Figure 5, which are slices close to the boundary. Due to inaccurate predicted axial view mask, the Mask-agg is too large in Figure 5f, but it can be improved with a more sophisticated filter than median filter. The inaccuracy of Mask-agg can result from the different resolution in images of test Subject 1 and 2 than the training set, and the small backbone architecture in GAN. We will improve both aspects in future work.

Conclusion

We showcase the segmentation performance by using the $$$\alpha$$$-confidence mask obtained by a conditional GAN and three-view aggregation. The performance is positively correlated with the human expert and negatively correlated with the VDP.

Acknowledgements

Funded by Novartis International AG.