4068
Robust and Computationally Efficient Missing Point and Phase Estimation for Multi-Channel Acquisition with ZTE Sequences1Champaign Imaging LLC, Shoreview, MN, United States, 2Radiology, University of Iowa, Iowa City, IA, United States, 3Electrical and Computer Engineering, University of Iowa, Iowa City, IA, United States
Synopsis
Missing point estimation has been a part of Fourier Transform NMR and MRI since the beginning. FID based imaging sequences, such as the ZTE (zero echo time) sequence, are missing needed data points corresponding to the region around the center of K-space. In multi-channel ZTE acquisitions, this estimate must be made for each channel. Missing data can be estimated by separate reference scans (WASPI and PETRA) but require extra time. In dynamic acquisitions missing points are optimally estimated from the data itself. Here we investigate applying a method borrowed from solid state NMR to estimate the missing points.
Introduction
FID sequences such as ZTE posses many advantages including capturing signals from fast relaxing spins [1], efficient use of time [2; 3] and quite acoustic operation [4; 5]. They possess one major disadvantage, information from the start of the FID is missing or corrupted due to requirements for RF pulse time and T/R switching (ZTE) and gradient ramping (UTE) [6]. Hybrid methods use separate acquisition of the center of K-space, such as in WASPI and PETRA [7]. These methods produce very good results for anatomical scans but limit the ability to acquire dynamic data such as needed for DCE scans or motion correction [8]. Methods such as SWIFT can be used to acquire the center after a small number of acquired views [9] but are difficult to implement on clinical hardware. Estimation methods potentially offer the optimum solution for regenerate the missing data [7; 10] in dynamic time series acquisitions but have issues with numeric stability, especially in the presence of phase variation as well as additional modest computation for each view. Here we introduce a robust and computationally efficient missing point and phase estimation algorithm originating in the solid state NMR community for multi channel acquisition with ZTE imaging sequences [11].Methods
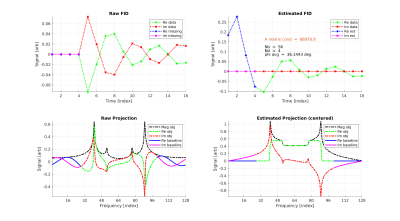
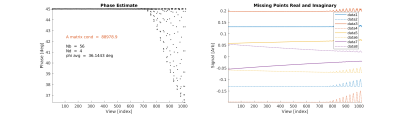
We modified a 3D Radial ZTE sequence [12] to accept table input for view-ordering. All simulated and acquired datasets were reconstructed using 2x oversampled gridding [13] with a radius 4 Kaiser-Bessel kernel and 50 iterations of the Pipe-Menon algorithm for sample density correction [14]. A hollow cube possessing internal slanted sides was simulated by direct synthesis of k-space data and reconstructed by gridding [8]. The modulation transfer function (MTF) in an orthogonal XY slice was estimated with the ImageJ plugin Slanted Edge MTF [15]. Contrast ratio and SNR were evaluated using 32x32 voxel patches in the center slice.In the Stoch/Olejniczak algorithm [11] the distorted FID first has the Nd missing/distorted points set to zero (see Fig. 1). The distorted projection is generated by FFT of the distorted FID. The algorithm utilizes the Nb point baseline region of the distorted projection, which excludes the region containing object signal, to estimate the missing points. When the points are correctly estimated this region has minimal real signal. The minimization is accomplished by pseudo inversion of a pre-computed 2*Nd by 2*Nd real matrix, much less numerically onerous than previous methods. Before the missing point estimate the constant phase must first be estimated by an initial deterministic minimization of the real component of the Distorted Projection utilizing multiplication by an Nb by Nb pre-computed complex matrix (see Fig. 2).
Results
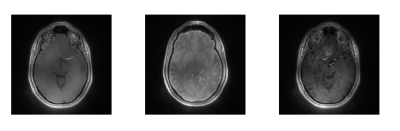
Phase and missing point accuracy, Contrast ratio, MTF performance, and SNR were evaluated before and after correction in the simulated cube object for Nd = 0, 1, 2, 3, 4... missing points up until numerical instability ( see Fig. 3). In-vivo images were evaluated for SNR and residual artifactual signal surrounding and contaminating the object.256^3 1mm^3 resolution Brain images of a health human volunteers were taken using Silent/ZTE using HEALPix view-order with intrinsic T1 weighting, inversion recovery and T2 preparations. Acquisitions were carried out at both 3T and 7T on GE discovery 750 and 950 systems respectively (See Fig. 4).
Example code available at: https://github.com/curtcorum/missing_points_phase
Conclusions and Future Work
The Stoch/Olejniczak algorithm performs well with coil compression. Iterateing between coil compression and missing point estimate and use of parallel imaging information are potential next steps.Acknowledgements
This work was funded in part by the SBIR Phase I grants R43MH115885 and R43MH122028 from the National Institute of Mental Health. Curt Corum and Champaign Imaging LLC are developing technology related to the topics reported. All in-vivo imaging was performed under an IRB-approved protocol at the University of Iowa, Magnetic Resonance Research Facility. We thank Mr. Stephen Otto of Champaign Imaging LLC for coordination and project management.References
[1] Du, J.; Bydder, M.; Takahashi, A. M.; Carl, M.; Chung, C. B. and Bydder, G. M. (2011). Short T2 contrast with three-dimensional ultrashort echo time imaging., Magn Reson Imaging 29 : 470-482.
[2] Corum, C. A.; Bauman, G.; Idiyatullin, D. S.; Hutter, D.; Everson, L. I.; Eberly, L. E.; Nelson, M. T.; Garwood, M.; Velikina, J. V. and Samsonov, A. A. (2015). High Spatial and Temporal Resolution Breast MRI with 3D Radial SWIFT Acquisition and Compressed Sensing MOCCO Reconstruction, (SWIFT-MOCCO).
[3] Corum, C.; Benson, J.; Idiyatullin, D.; Snyder, A.; Snyder, C.; Hutter, D.; Everson, L.; Eberly, L.; Nelson, M. and Garwood, M. (2015). High Spatial and Temporal Resolution Breast DCE MRI with SWIFT (SWeep Imaging with Fourier Transformation): a pilot study, Radiology 274 : 540-547.
[4] Alibek, S.; Vogel, M.; Sun, W.; Winkler, D.; Baker, C. A.; Burke, M. and Gloger, H. (2014). Acoustic noise reduction in MRI using Silent Scan: an initial experience., Diagn Interv Radiol 20 : 360-363.
[5] Costagli, M.; Symms, M. R.; Angeli, L.; Kelley, D. A. C.; Biagi, L.; Farnetani, A.; Rua, C.; Donatelli, G.; Tiberi, G.; Tosetti, M. and Cosottini, M. (2016). Assessment of Silent T1-weighted head imaging at 7~T., Eur Radiol 26 : 1879-1888.
[6] Chiang, J.-T. A.; Carl, M. and Du, J. (2013). Signal and contrast effects due to T2 decay during k-space readout of UTE (ultrashort TE) sequences., Magn Reson Imaging .
[7] Froidevaux, R.; Weiger, M.; Brunner, D. O.; Dietrich, B. E.; Wilm, B. J. and Pruessmann, K. P. (2017). Filling the dead-time gap in zero echo time MRI: Principles compared., Magnetic resonance in medicine.
[8] Corum, C. A.; Kruger, S. J. and Magnotta, V. A. (2019). HEALPix View-order for 3D Radial Self-Navigated Motion-Corrected ZTE MRI.
[9] Corum, C. A.; Idiyatullin, D.; Snyder, C. J. and Garwood, M. (2015). Gap Cycling for SWIFT, Magn Reson Med 73 : 677-682.
[10] Kuethe, D. O.; Caprihan, A.; Lowe, I. J.; Madio, D. P. and Gach, H. M. (1999). Transforming NMR data despite missing points., J Magn Reson 139 : 18-25.
[11] Stoch, G. and Olejniczak, Z. (2005). Missing first points and phase artifact mutually entangled in FT NMR data--noniterative solution., Journal of magnetic resonance (San Diego, Calif. : 1997) 173 : 140-152.
[12] Irie, R.; Suzuki, M.; Yamamoto, M.; Takano, N.; Suga, Y.; Hori, M.; Kamagata, K.; Takayama, M.; Yoshida, M.; Sato, S.; Hamasaki, N.; Oishi, H. and Aoki, S. (2014). Assessing Blood Flow in an Intracranial Stent: A Feasibility Study of MR Angiography Using a Silent Scan after Stent-Assisted Coil Embolization for Anterior Circulation Aneurysms., AJNR Am J Neuroradiol.
[13] Beatty, P. J.; Nishimura, D. G. and Pauly, J. M. (2005). Rapid gridding reconstruction with a minimal oversampling ratio, Medical Imaging, IEEE Transactions on 24 : 799 - 808.
[14] Pipe, J. G. and Menon, P. (1999). Sampling density compensation in MRI: rationale and an iterative numerical solution., Magn Reson Med 41 : 179-186.
[15] Mitja, C.; Escofet, J.; Tacho, A. and Revuelta, R. (2011). Slanted Edge MTF, .
Figures