Introduction

The method of bSSFP imaging is very powerful with various research and clinical applications, owing to its high efficiency, desirable contrast, and relative immunity to geometric distortion. However, it suffers from a notorious banding artifact due to sensitivity to main magnetic field inhomogeneity. Phase-cycled acquisitions were proposed to allow reduction of such artifact. Recently, an elliptical model¹ was introduced to eliminate banding artifact completely. This signal model has been further used to achieve mapping of certain physical parameters quantitatively². In order to unlock the bSSFP system, four or more phase-cycled acquisitions are typically needed^1,2,3 which prolong the total scan time, therefore any reduction of the number of acquisitions is desirable for improved efficiency. In this work, a general analytical solution was found from signal equations of only 3 phase-cycled bSSFP acquisitions. It has been verified using data from numerical simulations.

Method

Theory:
The measured complex signals from 3 phase-cycled bSSFP acquisitions can be described as¹,

$$P_{j}=\frac{M[1-ae^{i(\theta+\delta_{j})}]}{1-b\cos(\theta+\delta_{j})}\:\:\:\:\:\:\:\:\:\:\:\:j=1,2,3.\:\:\:\:\:\:\:\:\:\:\:(1)$$

where $$$M$$$ is the demodulated magnetization, $$$(a,b)$$$ are parameters related to relaxation times and flip angle, $$$θ$$$ is the common phase angle, and the three $$$δ$$$ angles are the known phase offset values¹. For simplicity, define new unknown variables $$$(x,y)=(b\cos\theta,b\sin\theta)$$$ and known parameters $$$(c_{j}, s_{j})=(\cos\delta_{j},\sin\delta_{j}), j=1,2,3.$$$ The numerators of Eqn.(1) can be written as $$$(J_{1},J_{2},J_{3})$$$ shown below,

$$J_{1}=P_{1}(1-xc_{1}+ys_{1}) \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(2)$$
$$J_{2}=P_{2}(1-xc_{2}+ys_{2}) \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(3)$$
$$J_{3}=P_{3}(1-xc_{3}+ys_{3}) \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(4)$$

While the 3 acquired complex data points $$$(P_{1},P_{2},P_{3})$$$ are known to be on an ellipse, it can be shown that the re-scaled 3 points $$$(J_{1},J_{2},J_{3})$$$ must be on a circle. We therefore have,

$$(J_{3}-J_{2})E=(J_{1}-J_{2}) \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(5)$$

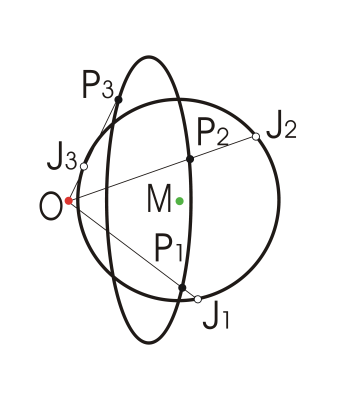
For equally distributed phase-cycling with $$$(\delta_{1},\delta_{2},\delta_{3})=(0,2\pi/3,4\pi/3)$$$, $$$E=\cos(\pi/3)+i\sin(\pi/3)$$$, a complex number with unity magnitude, representing a pure vector rotation of 60 degrees; otherwise E is readily determined by trigonometry based upon the 3 specific phase offset values. Figure 1 shows a specific example of such ellipse and circle, with $$$(a,b)=(0.9,0.7)$$$ and 3 equal distant phase-cycle offsets, where black dots indicate acquired $$$P$$$ points on an ellipse, and white dots are the re-scaled $$$J$$$ points along a circle forming an equal lateral triangle. Inserting Equations (2-4) into Equation(5), we obtain,

$$[P_{3}(1-xc_{3}+ys_{3})- P_{2}(1-xc_{2}+ys_{2})]E=P_{1}(1-xc_{1}+ys_{1})- P_{2}(1-xc_{2}+ys_{2})\:\:\:\:\:\:(6)$$

Splitting complex variables into real and imaginary parts, $$$P_{j}=R_{j}+iI_{j}$$$ and $$$E=E_{r}+iE_{i}$$$. From real part of Eqn.(6), we have,

$$E_{r}[R_{3}(1-xc_{3}+ys_{3})- R_{2}(1-xc_{2}+ys_{2})]+E_{i}[I_{2}(1-xc_{2}+ys_{2})- I_{3}(1-xc_{3}+ys_{3})]\\=R_{1}(1-xc_{1}+ys_{1})- R_{2}(1-xc_{2}+ys_{2})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(7)$$

and similarly from imaginary part,

$$E_{r}[I_{3}(1-xc_{3}+ys_{3})- I_{2}(1-xc_{2}+ys_{2})]+E_{i}[R_{3}(1-xc_{3}+ys_{3})- R_{2}(1-xc_{2}+ys_{2})]\\=I_{1}(1-xc_{1}+ys_{1})- I_{2}(1-xc_{2}+ys_{2})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(8)$$


Equations (7,8) can be converted into matrix form,


$$\begin{bmatrix}a_{11} & a_{12} \\a_{21} & a_{22} \end{bmatrix}\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}b_{1}\\ b_{2}\end{array}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(9)$$

where all coefficients are known to be,

$$a_{11}= E_{r}(R_{2}c_{2}-R_{3}c_{3})+E_{i}(I_{3}c_{3}-I_{2}c_{2})+(R_{1}c_{1}-R_{2}c_{2})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(10)$$

$$a_{12}= E_{r}(R_{3}s_{3}-R_{2}s_{2})+E_{i}(I_{2}s_{2}-I_{3}s_{3})+(R_{2}s_{2}-R_{1}s_{1})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(11)$$

$$a_{21}= E_{r}(I_{2}c_{2}-I_{3}c_{3})+E_{i}(R_{2}c_{2}-R_{3}c_{3})+(I_{2}c_{2}-I_{1}c_{1})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(12)$$

$$a_{22}= E_{r}(I_{3}s_{3}-I_{2}s_{2})+E_{i}(R_{3}s_{3}-R_{2}s_{2})+(I_{2}s_{2}-I_{1}s_{1})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(13)$$

$$b_{1}=R_{1}-R_{2}+E_{r}(R_{2}-R_{3})+E_{i}(I_{3}-I_{2})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(14)$$

$$b_{2}=I_{1}-I_{2}+E_{r}(I_{2}-I_{3})+E_{i}(R_{2}-R_{3})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(15)$$


Equation (9) can be solved as,


$$x= (a_{22}b_{1}-a_{12}b_{2})/ (a_{11}a_{22}-a_{12}a_{21})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(16)$$

$$y= (a_{11}b_{2}-a_{21}b_{1})/ (a_{11}a_{22}-a_{12}a_{21})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(17)$$


Once $$$(x,y)$$$ are obtained, it is straightforward to further find $$$(M,a,b)$$$, unlocking the system. For example, when $$$(\delta_{1},\delta_{2},\delta_{3})=(0,2\pi/3,4\pi/3)$$$, $$$M$$$ can be found simply as the mean value of $$$(J_{1},J_{2},J_{3})$$$ as shown in Figure 1.

Validation:
Complex bSSFP signals were generated from Equation (1) using equally spaced phase-cycling offsets of $$$(0,2\pi/3,4\pi/3)$$$ with a complete range for all physically possible values of parameters $$$(a,b)$$$ ¹, as shown in Figure 2. The unknown variables $$$(x,y)$$$ were first found as described above, leading to the demodulated magnetization $$$M$$$. This solution was compared with the ground truth of $$$M$$$ used in the simulation as well as the magnitude of the mean value of $$$(P_{1},P_{2},P_{3})$$$.

Results

The $$$M$$$ values obtained from the analytical solution agree well with the ground truth for all possible parameter settings of $$$(a,b)$$$, providing a preliminary validation of this approach. These results are presented in Figure 3, favorably compared with incompletely demodulated mean $$$M$$$ obtained by the naive operation of "complex sum".

Discussion

An analytical solution of the bSSFP problem is presented for data with only 3 general phase-cycled acquisitions. The 3 relative phase offsets can be of arbitrary values, although only equally spaced data were used in a numerical demonstration for simplicity. A key step of this approach is the introduction of Equation (5) as an additional constraint to the system. Previously, two independent analytical solutions were found for a 4-point system², implying redundancy of information and possibility of a solution from fewer acquisitions. Indeed this conjecture has now been mathematically proven. Future work includes further demonstration, optimization, and applications on experimental data acquired from phantoms and other subjects.

Conclusion

An analytical solution is found for bSSFP system with only 3 general phase-cycled acquisitions. It has been demonstrated with numerically simulated data, and is expected to be useful in future practical applications.

Acknowledgements

No acknowledgement found.