Introduction

Magnetic resonance imaging of the fetus is challenged by fetal and maternal motion, and is thus typically limited to single-shot imaging techniques such as HASTE¹ or SS-FSE. Restricted slice selective excitation reduces the encoding burden, and improves contrast or spatial resolution. Consequently, a good selective refocusing pulse will help eliminate the unwanted excitated voxels in the stopband.

In this work, we present numerical simulations of selective refocusing on a restricted slice pattern of 1.2cm thickness in the fetal brain by a joint optimization of a set of time-varying, spatially-nonlinear shim array fields² and a time-varying 2ms RF pulse with an auto-differentiable Bloch simulator framework³ without the presentence of the crusher gradient. Conventional refocusing pulse design methods, e.g, SLR⁴ has not been extended to the case of non-linearly varying shim fields. A decomposition property of the Bloch equation is exploited to overcome the undetermined initial magnetization problem by separately optimizing on three components, Mx, My and Mz. The selective refocusing profile achieves selective refocusing for 85% of voxels in the ROI (My< -0.9).

Method

Each coil in the shim array will generate a spatially non-linear B0 field which enriches the spatially selective ability and is only related to the applied current per coil. As employed in previous selective excitation design works⁵, the current in the shim array is optimized to generate a time-varying field to modify the spatial B0 distribution inside and outside the desired region. We also apply the concept of so-called alias de-selection techniques.

While the optimization-based design requires exact initial and desired magnetization for each voxel, the distribution of the initial magnetization is unknown for the refocusing pulse design due to several factors, e.g, B0 inhomogeneity and various TEs. To mitigate this problem, we investigate the linear/decomposition property of the Bloch equation on three components, Mx, My and Mz as Bloch equation describes a series of rotations, R = Rn…R1. To clarify this,
$$\left[\begin{array}{l}M x^{\prime} \\M y^{\prime} \\M z^{\prime}\end{array}\right]=R\left[\begin{array}{l}M x \\M y \\M z\end{array}\right]=R\left[\begin{array}{c}M x \\0 \\0\end{array}\right]+R\left[\begin{array}{c}0 \\M y \\0\end{array}\right]+R\left[\begin{array}{c}0 \\0 \\M z\end{array}\right] = \left[\begin{array}{l}M x 1^{\prime} \\M y 1^{\prime} \\M z 1^{\prime}\end{array}\right] + \left[\begin{array}{l}M x 2^{\prime} \\M y 2^{\prime} \\M z 2^{\prime}\end{array}\right]+ \left[\begin{array}{l}M x 3^{\prime} \\M y 3^{\prime} \\M z 3^{\prime}\end{array}\right]$$
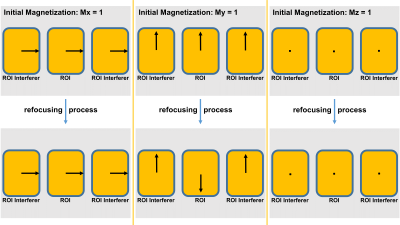
Specifically, for a selective refocusing pulse design with x axis as the rotation axis, the following requirements should be satisfied as shown in figure 1.

1. The X component should remain the same in both ROI and ROI interferers: Before, Mx = 1; After, Mx = 1.
2. The Y component should reverse in the ROI: Before, My = 1; After, My = -1; The Y component should remain the same in the ROI interferers: Before, My = 1; After, My = 1.
3. The Z component should not generate transverse components in both ROI and ROI interferers: Before, Mz = 1; After, Mz = 1/-1.

The optimization could be formulated as below for any initial magnetization distributions,
$$ \underset{I \in \mathbb{R}^{n_{T} \times n_c}, b \in \mathbb{C}^{n_{T}}}{\arg \min }\mathcal{L}=||W*Mx-W*Mx_d|| + ||W*My-W*My_d|| + 0.5*||W*Mz_{xy}|| +\mathcal{R}(b)$$
where $$$Mx$$$, $$$My$$$ are the magnetization distribution actual profile generated by the RF and time-varying nonlinear B field using time-discrete Bloch simulator with the initial magnetization $$$Mx = 1$$$ and $$$My = 1$$$, respectively. $$$Mx_d$$$, $$$My_d$$$ are the desired magnetization distribution. $$$Mz_{xy}$$$ is the transverse magnetization distribution with the initial magnetization $$$Mz = 1$$$. $$$W$$$ is the loss weight of ROI and ROI interferers.$$$I$$$ is the shim coil current. $$$b$$$ is the RF pulse. $$$n_T$$$ is the number of time points and $$$n_c$$$ is the number of shim coils. $$$\mathcal{R}(b)$$$ is the regularizer.

Results and Discussions

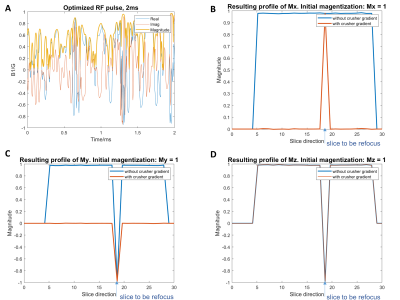
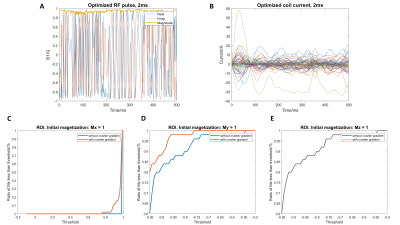
In this work, we conduct the validation experiments on a 30*30*20 voxel grid with the full FOV of 36*36*24 cm³. The restricted fetal brain slice is about one third of the full FOV. 64 ($$$n^c$$$) shim coils are randomly placed along the mother’s abdominal area to make the non-linear shim field cover as much space as possible. There are 500 time points ($$$n^T$$$) for the RF pulse. In the ROI, $$$W = 2$$$; in the ROI interferers, $$$W = 0.5$$$. Details can be checked in figure 2.

We first show that decomposition theory works by designing a slice-selective refocusing pulse via optimization only on a time-varying RF pulse. Figure 3 shows that all the grids are perfectly refocused even without the presentence of crusher gradient. However, as the resolution is 1.2cm, the pulse may not successfully refocus all grids at a finer resolution.
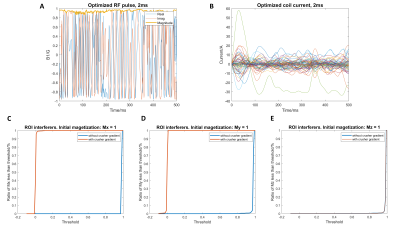
Further we show the design of selective refocusing pulse for the restricted slice of fetal brain. Both the RF pulse and shim coil current are optimized. Figure 4 shows the results of the slice profile in the ROI based on decomposition theory with different crusher gradient conditions. Figure 5 shows the results of the slice profile in the ROI interferers (not refocusing regions).

Conclusions

Selective refocusing pulse helps further improve acquired signal and images. In this work, we designed the RF pulse and the spatially non-linear time-varying shim array field by auto-diff for selective refocusing in a restricted fetal brain slice. We proposed decomposition theory to solve the undetermined initial magnetization distribution which achieves satisfying refocusing results.

Acknowledgements

This work was supported in part by research grants NIH R01 EB017337, U01 HD087211, R01HD100009.