Introduction

Accelerated MR data acquisition methods have enabled significant gains in spatial and temporal resolution and imaging efficiency. For data sampled using multiple receiver channels, the GRAPPA¹ method for recovering in-plane acceleration and slice-GRAPPA² for recovering Simultaneous Multi-Slice (SMS) accelerated data are both based on the application of a convolution kernel in k-space that synthesizes un-aliased data from a linear combination of sampled multi-channel data. Slice-GRAPPA formulates the slice separation problem similar to the formulation of conventional GRAPPA for in-plane data recovery, utilizing slice collapsed data in the MB reconstruction problem as analogous input to the aliased data in the in-plane data recovery problem. It was later observed that signal leakage in the original slice-GRAPPA formulation could be resolved by imposing a "LeakBlock" constraint³ to reduce signal contributions between the simultaneously-acquired slices in the reconstruction. This work seeks to explain the relationship between the original slice-GRAPPA method, the LeakBlock method, and in-plane GRAPPA.

Theory

Consider a blipped-CAIPI⁴ MB=2 acquisition where one of the two acquired slices is shifted by 1/2 the FOV. As the gap between the excited slices is reduced, the two slices will slowly approach similarity until, at the limit, the two slices will have identical information, but with one version shifted by 1/2 FOV relative to the other. By the Fourier shift theorem, an image-domain shift by 1/2 FOV corresponds to an alternating sign-change occurring between consecutive lines of k-space. E.g. the phase of each line of k-space data in the shifted slice will alternate as $$$\{+1,-1,+1,-1,+1,-1,\cdots\}$$$ relative to the original non-shifted slice. If one synthetically collapses these two slices together to form a synthetic zero-slice-gap MB=2 acquisition, the k-space lines with alternating phase from one slice will cancel half of the lines from the other slice. In the spatial domain, the aliasing pattern in this synthetic zero-gap SMS image will be visibly identical to an R=2 sub-sampled version of k-space.
Mathematically, the associated normal equations are as follows. From Cauley et al.³, the original slice-GRAPPA algorithm is $$(A_1 + A_2 + \cdots + A_S ) g_t = ( \Sigma_{s=1}^S A_s ) g_t = b_t$$ where the excited slices are combined during acquisition, and the GRAPPA coefficients, $$$g_t$$$, separate them to form the desired un-aliased target data, $$$b_t$$$ for slice $$$t$$$. The corresponding normal equations are $$ \left( \sum_{s=1}^S A_s \right)^H \left( \sum_{s=1}^S A_s \right) g_t = \left( \sum_{s=1}^S A_s \right)^H b_t.$$
By contrast, the slice-GRAPPA LeakBlock implementation seeks to identify GRAPPA coefficients that both generate the target slice of interest, $$$A_t g_t = b_t$$$, while constraining the other slices to be identically zero, $$$A_s g_t = 0$$$ for $$$s \neq t$$$. In this case, the associated normal equations are $$ \left( \sum_{s=1}^S A_s^H A_s \right) g_t = A_t^H b_t . $$

To relate to inplane-GRAPPA, consider the MB=2 zero-slice-gap example above, with the corresponding normal equations
$$ (A_1 + A_2 )^H (A_1 + A_2 ) g_t = (A_1 + A_2 )^H b_t $$ for original slice-GRAPPA versus $$(A_1^H A_1 + A_2^H A_2 ) g_t = A_t^H b_t $$ for LeakBlock.

Structurally, these two linear system matrices are quite different. The phase change in alternate k-space lines of the 1/2 FOV-shifted slice result in signal cancellation in the ($$$A_1+A_2$$$) matrix that appears in the original variant. In LeakBlock, by contrast, each of the source data matrices are first multiplied by their conjugate-transpose (i.e., $$$A_1^H A_1$$$) prior to the summation. The ensures that the self-product of the 1/2 FOV-shifted slice, $$$A_2^H A_2$$$, identically matches that of the original slice because $$$\{+1,-1,+1,-1,\cdots\}^2 = \{+1,+1,+1,+1,\cdots\}$$$. This reveals that the LeakBlock formulation reduces to $$$2(A^H_t A_t) g_t = A_t b_t,$$$ which is identically equivalent structurally to the normal system of equations used for inplane-GRAPPA data recovery. This result can be generalized to state that in the zero-slice-gap case, a synthetic blipped-CAIPI acquisition will reduce to an accelerated acquisition when the acceleration rate, R, is equal to the number of synthetic slices, MB, when LeakBlock is employed.

Results

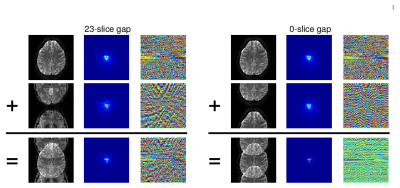
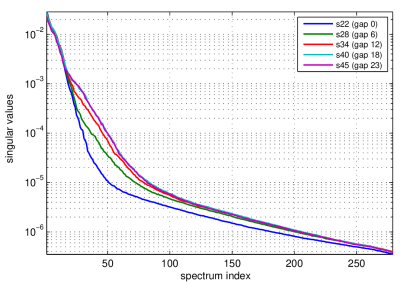
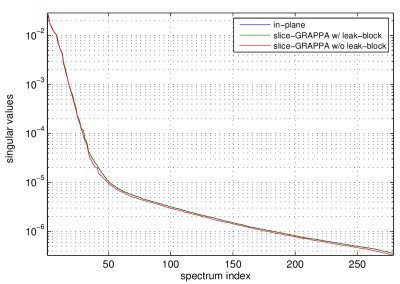
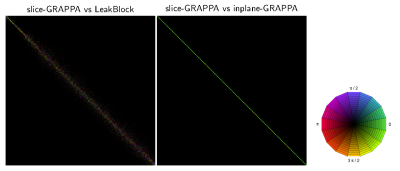
A visualization of the synthetic zero-gap MB=2 experiment is illustrated in Figure 1. Note that in both the image and k-space domains, the zero-gap MB=2 images look identical to R=2 inplane accelerated images. Figure 2 illustrates how the singular value spectrum of the linear system matrix changes as the MB=2 gap is reduced to zero. Note that the condition number stays comparable, but the subspace of support decreases as the slice gap shrinks. Figure 3 illustrates the system spectra for all three cases, with only the slice-GRAPPA system showing slight differences to the other two. The equivalence between LeakBlock and inplane-GRAPPA is further confirmed in Figure 4, which shows matrix cross-correlations between the Eigen-vectors of each system. Notably, there is significant structural divergence between the slice-GRAPPA and LeakBlock systems, but none between LeakBlock and inplane-GRAPPA.

Conclusion

This work demonstrates the link between SMS slice-separation and in-plane data recovery when using GRAPPA reconstruction kernels. It demonstrates that while the goals and formulation may be different, the two methods are in-fact linked and produce the same system matrix to identify reconstruction coefficients in the limiting case of zero-slice-gap. Understanding this relationship can help guide SMS and inplane regularization⁵ strategies to balance SNR and image quality.