Introduction

Reconstruction of signal dynamics from fast-spin-echo acquisitions yields improved image quality and enables quantitative mapping¹, but requires lengthy scan times. T2-shuffling reconstructs a time-series of T2-weighted images within clinically feasible scan times by incorporating a low-rank subspace into the forward model that significantly reduces the degrees of freedom. However, T2-shuffling will incur reconstruction artifacts at higher acceleration rates, particularly in 2D acquisitions.

Supervised machine learning achieves impressive reconstruction quality, but the lack of acquiring training data often precludes its use in the T2-shuffling regime. Recently Yaman et al.^2,3 proposed a zero-shot self-supervised learning method (ZSSS) for MRI reconstruction by exploiting partitions of the measured k-space itself.

In this work, we combine the T2-shuffling forward model into the ZSSS framework, enabling self-supervised, learning-based reconstruction of signal evolution from T2-shuffling data. Simulated reconstruction experiments suggest that ZSSS combined with the subspace model outperforms standard T2-shuffling and ZSSS without the subspace model at varying acceleration rates.

Methods

T2 Shuffling Model
T2 shuffling assembles the signal evolution for realistic T1 and T2 values into a dictionary and approximates the low rank subspace $$$\Phi \in C^{T \times B} $$$ by singular vector decomposition (SVD), where $$$T$$$ is the number of echoes and $$$B$$$ is the number of basis. The series of T2 weighted images $$$x \in C^{M \times N \times T}$$$ ($$$M,N$$$ are the height and width of images) to be reconstructed can be projected onto $$$\Phi$$$ yielding coefficients $$$\alpha \in C^{M \times N \times B}$$$ and the forward model becomes
$$y=R F S \Phi \alpha$$
where $$$y \in C ^{ M \times N \times C \times T}$$$ is the acquired kspace data, $$$F$$$ is Fourier operation, $$$S$$$ is the coil sensitivity map, $$$R$$$ is the undersampling mask.

Zero-shot self-supervised learning framework (ZSSS)
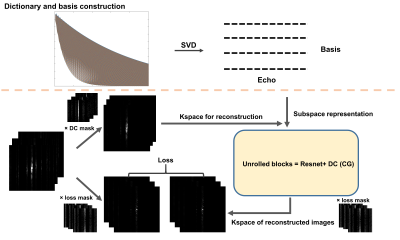
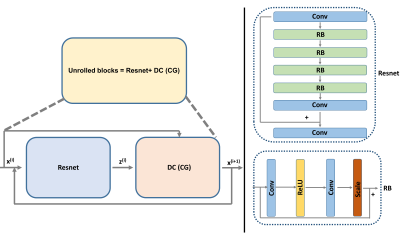
The zero-shot self-supervised learning framework is adopted and extended in this work, as shown in figure 2. The undersampled kspace data are divided into two disjoint subsets, $$$\Theta$$$ for the data consistency units and $$$\Omega$$$ for training loss. Note that the division is dynamic during the training as there is a lack of separate training data. The reconstruction is separated into two parts:
$$\mathbf{z}^{(i-1)}=\arg \min _{\mathbf{z}} \mu\left\|\mathbf{x}^{(i-1)}-\mathbf{z}\right\|_{2}^{2}+\mathcal{R}(\mathbf{z})$$
$$\mathbf{x}^{(i)}=\arg \min _{\mathbf{x}}\left\|\mathbf{y}_{\boldsymbol{\Omega}}-\mathbf{E}_{\boldsymbol{\Omega}} \mathbf{x}\right\|_{2}^{2}+\mu\left\|\mathbf{x}-\mathbf{z}^{(i-1)}\right\|_{2}^{2}$$
The definition of variables can be seen from previous works².

Proposed method
To mitigate the large number of degrees of freedom and poor conditioning, we incorporate the low rank T2 shuffling model into the zero-shot self-supervised learning framework as shown in figure 1.
$$\mathbf{z}^{(i-1)}=\arg \min _{\mathbf{z}} \mu\left\|\alpha^{(i-1)}-\mathbf{z}\right\|_{2}^{2}+\mathcal{R}(\mathbf{z})$$
$$\alpha^{(i)}=\arg \min _{\alpha}\left\|\mathbf{y}_{\boldsymbol{\Omega}}-\mathbf{E}_{\boldsymbol{\Omega}} \Phi \alpha\right\|_{2}^{2}+\mu\left\|\alpha-\mathbf{z}^{(i-1)}\right\|_{2}^{2}$$
Our proposed method adopts the advantages of subspace constraints and strong representative ability of deep neural networks.

Experiments

Dictionary and subspace constructions
The dictionary of the TSE signal evolution for realistic T1 and T2 values is generated using extended-phase-graph (EPG) simulations^4,5. For the dictionary, T2=5-400 ms, T1=1000 ms, 10 echoes, 160 degree refocusing pulses, and 4.8ms echo spacing. The dictionary is used to generate the subspace using SVD with the number of basis vectors, B = 2,3,4.

Simulated Reconstruction Experiments
In this work, we conduct the experiments using EPG to simulate a series of kspace for each echo of a FSE sequence with T=10 echoes, 4.8ms echo spacing, 160 degree refocusing pulses and 8 channel coil. For the k-space of each echo, we apply a mask with random phase encoding acquisition points with the acceleration rate R = 8 and 16. The full FOV is 256x256 with the resolution of 1mmx1mm.

For the zero-shot self-supervised learning framework, The number of unrolled blocks and resnet blocks is 4 and 4 respectively. The iteration of conjugate gradient (CG) is 12. The subsets of undersampled kspace are different and dynamic during the training process for each kspace at different echoes.

We compared four models to show the superiority of our proposed method
1. Reconstruction using conventional T2 shuffling subspace.
2. Reconstruction using ZSSS on single images (ZSSS-s).
3. Reconstruction using ZSSS on the whole series of images (ZSSS-m).
4. Reconstruction using ZSSS with subspace constraints on the whole series of images (ZSSSSub), i.e., the proposed method.

Results and Discussions

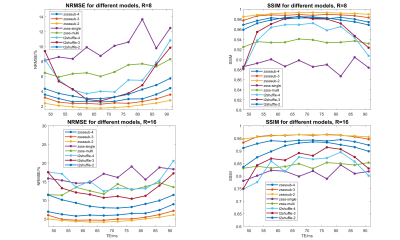
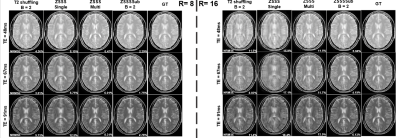
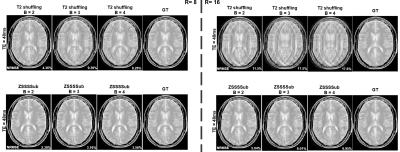
Figure 3 shows the RMSE and SSIM for 10 echo images for R = 8 and 16 with all four methods. Our proposed method achieves the best results among all experiments. It could be seen from the results that the representative power of neural networks can be utilized when the subspace constraints are imposed. Also, the model with B = 2 outperforms the models with B = 3 and 4 due to conditioning issues.

Figure 4 shows the reconstructed examples from the four methods (B = 2). Our proposed method significantly reduces the artifacts and improves the image quality, especially at higher acceleration rates.

Figure 5 shows the reconstructed examples with different basis numbers. The conditioning number is a big issue for the reconstruction. Fewer bases result in better conditioning and improved image quality.

Conclusions

In this work, we proposed a novel technique for the reconstruction of a series of T2 weighted images from a single FSE scan via zero-shot self-supervised learning with the incorporation of subspace constraints. The reconstruction results show the superiority of the proposed method in image quality and artifacts reduction, especially at higher acceleration rates.

Acknowledgements

This work was supported in part by research grants NIH R01 EB017337, U01 HD087211, R01HD100009.