4045
Sinogram Transformers: Accelerating Radial MRI using Vision Transformers1Computer Science, University of Arizona, Tucson, AZ, United States, 2Electrical and Computer Engineering, University of Arizona, Tucson, AZ, United States, 3Biomedical Engineering, University of Arizona, Tucson, AZ, United States, 4Medical Imaging, University of Arizona, Tucson, AZ, United States, 5Applied Mathematics, University of Arizona, Tucson, AZ, United States
Synopsis
The aim of this work is to investigate the used of Transformer architectures in radial image reconstruction. While most deep-learning image reconstruction methods are based on convolutional neural networks (CNNs), recent advances in computer vision suggest that Transformer architecture may provide a favorable alternative in many vision tasks. In this work, we demonstrate that Transformer architectures can be used for sinogram interpolation and yield results comparable to CNNs.
Introduction
Radial k-space sampling techniques are increasingly used in dynamic imaging1,2 and quantitative parameter mapping applications3,4 due to their robustness to motion and their ability to achieve high spatial/temporal resolution using limited data. Deep learning-based MRI (DL-MRI) reconstruction techniques5,6,7,8 have been introduced for radial MRI. In contrast to the previous generation of constrained reconstruction methods, DL-MRI reconstruction techniques yield improved reconstruction quality together with fast reconstruction times. With the notable exception of AUTOMAP7, most DL-MRI reconstruction methods rely on convolutional neural networks (CNNs). Recently, inspired by the success of the Transformer networks in Natural Language Processing applications, the computer vision community started to investigate the use of Transformer networks in vision applications9. In this work, we investigate the use of Transformer networks for reconstruction of radial MRI. In particular, we compare CNNs and Transformer networks on the task of sinogram learning for accelerating radial MRI.Methods
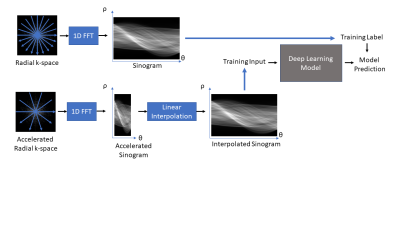
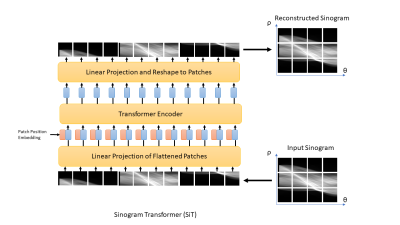
The proposed sinogram learning pipeline is illustrated in Figure 1. A 2D image slice was first transformed to k-space using Non-Uniform FFT to simulate k-space acquisition using sufficient number of radial views to satisfy Nyquist sampling. Each radial view was then transformed to sinogram domain using 1D FFT. This sinogram was used as a label during deep learning model training. This sinogram was undersampled along the view dimension to simulate accelerated radial MRI. The unacquired radial views were then created using linear interpolation to form an interpolated sinogram, which was used as input to the deep learning model training. The deep learning models were trained using supervised training. The CNN model was a Unet11 with contracting and expansive paths connected with skip connections. The architecture of our proposed sinogram Transformer (SiT) is shown in Figure 2. The first step in this architecture is the partitioning of the input sinogram into non-overlapping patches. Each patch is then flattened and passed through a (learned) linear transform. The transform coefficients are combined with patch position embeddings and processed using a Transformer encoder, which consists of multiple layers of multi-head self attention and multilayer perceptrons (MLPs).3D T1-weighted datasets of the brain acquired as part of the OASIS-3 study10 were used. Roughly 360,000 128x128 2D slices were extracted from the image volumes and split into training and validation datasets with approximately 90%/10% split. A separate dataset obtained from 1000 slices were used for testing. Fully sampled sinograms with 290 views and 185 steps were created using Radon transform. These datasets were zero-padded to 304x192 to enable multi-scale processing in Unet and 4X undersampling was used to simulate accelerated data acquisition. The Unet had four multi-resolution scales and the first scale had convolutional blocks with 32 filters. The transformer model used 16x16 patches, linear transforms with 128 coefficients, and 16 transformer layers. The Adam optimizer with batch size = 128 was used to train each network for up to 100 epochs with cosine weight decay with two epoch initial warmup and base learning weight = 10-5. An early stopping was adopted when the mean absolute error loss improvement fell below 10-5. The networks were implemented in Python using Tensorflow/Keras and executed on NVIDIA RTX A6000 GPUs. Once the networks were trained, they were used to predict the unacquired views of the sinograms in the test cohort and images were generated using inverse Radon transform. Structural Similarity Index (SSIM) between the reference image and accelerated reconstructions were computed.
Results and Discussion
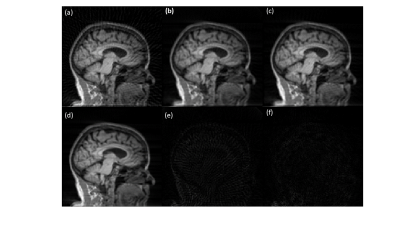
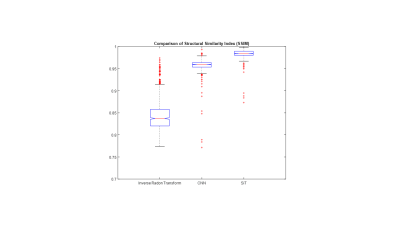
A sample slice reconstructed using different techniques is shown in Figure 3. Figure 3(a) shows the inverse Radon transform of the 4X accelerated sinogram, where streaks due to undersampling are clearly visible. Figures 3(b) and 3(c) show images obtained using CNN and SiT based processing of the undersampled sinograms. The undersampling artifacts are reduced in both cases. Figure 3(d) shows the reference slice obtained using sufficient number of radial views to satisfy Nyquist sampling. The absolute error maps (5X amplified for display) corresponding to the CNN and SiT images are shown in Figures 3(e) and 3(f), respectively.Figure 4 provides a comparison between SSIM values obtained using the Radon transform on the accelerated data, Radon transform of the CNN interpolated sinogram, and Radon transform of the SiT interpolates sinogram. While both deep learning approaches provide substantial improvement in SSIM, SiT results in higher SSIM values on average.
Although CNNs have inductive biases such as translation equivariance and locality, these biases are often achieved at the expense of discarded information during strided convolutions or max pool operations, and limited ability to connect non-local information. While other DL approaches such as AUTOMAP allow effective utilization of non-local information, the dense layers required for these approaches result in high memory and computational requirements. The Transformer architectures provide a good comprise between CNNs and densely connected networks, particularly in applications such as sinogram learning, where correlations are not necessarily localized.
Conclusions
We have shown that Transformer architectures can be a viable alternative to CNNs for sinogram interpolation. In this application, where the signal correlations are not necessarily localized, the Transformer architectures achieved favorable results in comparison to CNNs.Acknowledgements
We would like to acknowledge grant support from NIH (CA245920), the Arizona Biomedical Research Commission (CTR056039), NSF (DMS-1937229, Research Experiences for Undergraduates), and the Technology and Research Initiative Fund Technology and Research Initiative Fund (TRIF). Data were provided by OASIS-3: Principal Investigators: T. Benzinger, D. Marcus, J. Morris; NIH P50 AG00561, P30 NS09857781, P01 AG026276, P01 AG003991, R01 AG043434, UL1 TR000448, R01 EB009352.References
1. Song HK, Dougherty L. Dynamic MRI with projection reconstruction and KWIC processing for simultaneous high spatial and temporal resolution. Magn Reson Med. 2004 Oct;52(4):815-24. doi: 10.1002/mrm.20237. PMID: 15389936.
2. Lin W, Guo J, Rosen MA, Song HK. Respiratory motion-compensated radial dynamic contrast-enhanced (DCE)-MRI of chest and abdominal lesions. Magn Reson Med. 2008 Nov;60(5):1135-46. doi: 10.1002/mrm.21740. PMID: 18956465; PMCID: PMC4772667.
3. Altbach MI, Outwater EK, Trouard TP, et al. Radial fast spin-echo method for T2-weighted imaging and T2 mapping of the liver. J Magn Reson Imaging. 2002;16(2):179-189. doi:10.1002/jmri.10142
4. Z Li, A Bilgin, K Johnson, J Galons, S Vedantham, DR Martin, MI Altbach, “Rapid High-Resolution T1 Mapping Using a Highly Accelerated Radial Steady-State Free-Precession Technique,” Journal of Magnetic Resonance Imaging, 49: 239-252, 2018. https://doi.org/10.1002/jmri.26170
5. Fu Z, Mandava S, Keerthivasan MB, et al. A multi-scale residual network for accelerated radial MR parameter mapping. Magn Reson Imaging. 2020;73:152-162. doi:10.1016/j.mri.2020.08.013
6. Knoll F, Hammernik K, Zhang C, et al. Deep-Learning Methods for Parallel Magnetic Resonance Imaging Reconstruction: A Survey of the Current Approaches, Trends, and Issues. IEEE Signal Process Mag. 2020;37(1):128-140. doi:10.1109/MSP.2019.2950640
7. Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS. Image reconstruction by domain-transform manifold learning. Nature. 2018 Mar 21;555(7697):487-492. doi: 10.1038/nature25988. PMID: 29565357.
8. Kim T, Eo T, Park D, Jun Y, and Hwang D. Deep Sinogram Learning for Radial MRI: Comparison with k-space and Image Learning. Proceedings of the 2018 ISMRM. Abstract 2799.
9. Dosovitskiy A, Beyer L, Kolesnikov A, Weissenborn D, Zhai X, Unterthiner T, Dehghani M, Minderer M, Heigold G, Gelly S, et al., “An image is worth 16x16 words: Transformers for image recognition at scale,” arXiv preprint arXiv:2010.11929, 2020.
10. LaMontagne, Pamela J. et. al. OASIS-3: Longitudinal Neuroimaging, Clinical, and Cognitive Dataset for Normal Aging and Alzheimer Disease, medRxiv preprint, 2019 doi:10.1101/2019.12.13.19014902
11. Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. Medical Image Computing and Computer-Assisted Intervention (MICCAI), Springer, LNCS, Vol.9351: 234--241, 2015.
Figures