3951
Optimized variable winding pitch coil designs for miniature B0 field modification.1Department of Radiology, Medical Physics, Medical Center – University of Freiburg, Freiburg, Germany, 2Neurozentrum, Medical Center – University of Freiburg, Freiburg, Germany, 3High Field MR Center, Center for Medical Physics and Biomedical Engineering, Medical University of Vienna, Vienna, Austria
Synopsis
We present numerical optimization of variable winding pitch coil designs for miniature coils with respect to target field homogeneity. The optimization is based on a continuous coil winding layout that was used to simulate field homogeneity in the target volume via the Biot-Savart law. The example coil designs expand the range of applications for frequency adjustable field probes, as they increase the B0 modification field’s homogeneity by factor of 7. Due to the specific requirements of miniature B0 modification coils, the dimensions of the coil are restricted in length, width and wire diameter.
INTRODUCTION:
The geometric constraints of miniature solenoids ultimately limit the field homogeneity in any target field volume. The presented method finds a variable winding pitch design that maximizes field homogeneity in the target field volume of such a geometric constrained miniature coil. The presented method relies on a continuous winding design which accounts for interconnections of the coil windings.The variable winding pitch approach was inspired by a coil manufacturing technique, that relies on a dissolvable 3D-printed coil former, as presented by Kelz et al. 1. However, even though four different variable winding pitch examples were build, Kelz et al. did not optimize the winding pitch for a specific target volume. A similar approach relying on variable winding pitch, had been taken by Idziak et al. as well, for the design and construction of a RF coil for solid-state NMR 2.The coil designs discovered in this work can for example be used to improve the B0 modification coils used in frequency adjustable field probes 3. This potentially expands the possible range of applications for frequency adjustable field probes1, as they will enable B0 field modification with improved field homogeneity and thus longer T2* during the measurements. Due to the small size of the coil and expected driving current in the range 100 mA, the dimensions of the coil design are restricted in coil length, width and wire diameter.
METHODS:
This study compares the magnetic field homogeneity of optimized regular winding pitch and optimized variable winding pitch coils in Biot-Savart simulations. The winding pitch was optimized with regard to maximum field spread per B0 field shift in the target volume. The maximum field spread per B0 field shift describes the difference of the maximum and the minimum field strength in the target volume divided by of the field strength of the center voxel. The maximum field spread per B0 field shift is minimized in the optimization process.The coil description considers the coil in an unwrapped state. The unwrapping allows to describe the variable winding pitch as a function that can be modeled by polynomials. The coil in its unwrapped and wrapped state is illustrated in Figure 1.
The regular winding pitch in its unwrapped state corresponds to a straight line with a steady slope c described by $$$f_1$$$:
$$\mathbf {f_1} (\mathbf {z} )={c} {\mathbf {z} } ,$$
$$\mathbf {f_1'} (\mathbf {z} )={c} .$$
Additional, position dependent polynomial terms allow to modify the slope of the function and therefore the winding pitch of the coil. An additional cubed term stretches the center windings and compresses the windings towards the end of the coil. $$$f_2$$$ is an example of this modulated winding pitch with the additional term $$$a · z^{3}$$$ and the coefficient $$$b$$$:
$$\mathbf {f_2} (\mathbf {z} )={a} {\mathbf {z} ^{3}} + {b} {\mathbf {z}} ,$$
$$\mathbf {f_2'} (\mathbf {z} )=3{a} {\mathbf {z} ^{2}} + {b} .$$
The manufacturing of a coil with a 3D printed dissolvable former as shown in 1 is typically used to build single layer coils. Inside such a layer, the maximum slope c max of the coil is constrained by the wire thickness d:
$$c_{max} = {\frac {2\pi {R_{coil}}}{d_{wire}} } .$$
Furthermore, the minimum slope c min was constrained to allow for only one winding direction:
$$c_{min} = 0 .$$
Combining function $$$f_1'$$$ and $$$f_2'$$$ results in the non linear constraint:
$$c_{min} \leq \ 3a\mathbf {z}^{2} + {b} \leq\ c_{max} .$$
The resulting nonlinear optimization problem was initialized at multiple randomly initialized values to improve the global optimization behavior. The corresponding Matlab program for the presented variable winding pitch coil optimization can be found on https://github.com/Nikbert/solenoidPitchOptimization.
The presented examples were calculated for a spherical target volume with diameter of 1.4 mm and a coil length of 4 mm. The diameter was varied from 2 mm to 4 mm in 0.2 mm steps. The coil elements were divided into 3600 segments. The grid resolution for the simulation was set to 60×60×60 voxel for a 4×4×4 mm3 volume. This was chosen as a trade-off between resolution and simulation time had to be made.
RESULTS and DISCUSSION:
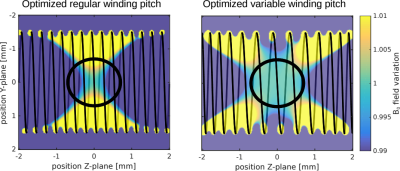
Simulated B0 fields for optimized regular and variable winding pitch coil designs are illustrated in Fig. 2. The presented optimization approach for variable winding pitch coil designs can reduce the maximum relative field variation inside the target volume by a factor of 7 and more compared to regular winding pitch designs for the constrains chosen in this example. Fig. 3 makes it apparent that the variable winding pitch approach can yield the best improvement with a coil aspect ratio of 4/3 (length/diameter) resulting in an improvement factor of 8.4 by changing to the variable winding pitch design. However, the optimized coil design highly depends on the geometry of the target volume.CONCLUSION:
Variable winding pitch coil designs can significantly improve the field homogeneity in the target volume, depending on the available coil length to target field aspect ratio. With the presented program it is possible to evaluate the homogeneity improvement using individual design constrains.Acknowledgements
The project was funded by the German Federal Ministry of Education and Research under grant number 13GW0356B. The author is responsible for the content of this publication. The authors acknowledge Matthias Pfefferle for keeping the servers running.References
1. Kelz J., 3D-printed dissolvable inserts for efficient and customizable fabrication of NMR transceiver coils, Journal of Magnetic Resonance, p. 4, 2019.
2. Idziak S., Haeberlen U., Design and construction of a high homogeneity rf coil for solid-state multiple-pulse NMR, Journal of Magnetic Resonance, vol. 50, pp. 281–288, Nov. 1982.
3. Wehkamp N., Rovedo P., Fischer E., et al, Frequency-adjustable magnetic field probes, Magnetic Resonance in Medicine, vol. 85, p1123-1133, 2021
Figures

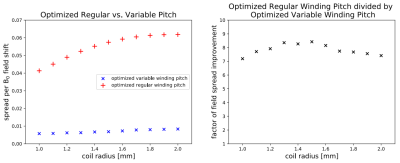
Left side: Spread per B0 field shift for the regular and optimized variable winding pitch coildesign. The coil length was constant at 4 mm and the coil radius was varied from 1 to 2 mm.
Right side: Factor of field spread improvement of the optimized variable winding pitch coil design in relation to the optimized regular winding pitch coil design.