Introduction

Magnetic Resonance Elastography (MRE) and Diffusion Tensor Imaging (DTI) are two non-invasive MRI techniques that use the phase and magnitude of the complex-valued MRI signal, respectively. The simultaneous acquisition of MRE and DTI is beneficial by reducing the total scanning time by 50% and providing immediately co-registered images. We previously have shown the feasibility of simultaneous acquisition of DTI and MRE, which we name DTI-MRE, on in vivo human brain .^1,2 In this work we simulated the performance of gradients with various gradient moment nulling (GMN) characteristics and identified optimized experimental parameter sets for in vivo human brain DTI-MRE. In the presented preliminary study, we compare two aspects: one is the performance of phase images between DTI-MRE with a single trapezoidal gradient and conventional flow-compensated MRE; the other is the performance between two experimental DTI-MRE parameter sets we classify as good and moderate.

Methods

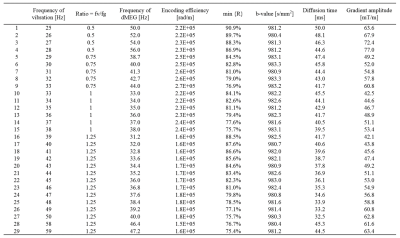
The GMN simulation used the symbolic math toolbox in MATLAB (MathWorks, MA). The conditions for finding the experimental parameter sets are a b-value within the range of 980-1020 s/mm²,an encoding efficiency of vibration above 1.5x10⁵ rad/m, vibration frequencies within range of 20-70 Hz, and a separation time between motion encoding gradients (MEGs) selected to be integer multiples of vibration periods.⁴ The parameter sets were identified based on the extent of vibration-induced signal loss min{R(x)}, which is listed in Table 1 and was calculated using an equation that was described previously.³ Two sets of the simulation results were selected as Good (min{R(x)} = 87.6%) and Moderate (min{R(x)} = 75.7%) for performance comparison in one volunteer as shown in Table 2.
The experimental DTI-MRE study on in vivo human brain was approved by the Institutional Review Board (Protocol # 2018-1042) at the University of Illinois at Chicago. The study was conducted on a 3T human scanner (Prisma, Siemens). A modified single-shot, spin-echo echo planar imaging (SS-SE-EPI) sequence for DTI-MRE was used in this study. Conventional MRE with flow compensation and DTI-MRE were acquired at the same frequency of 50 Hz without fractional encoding. The echo time (TE), matrix size, voxel size and number of slices were 78ms, 100 100, 2.5 2.5 2.5 mm³ and 48, respectively. The gradient amplitudes for MRE and DTI-MRE were 78/1000 mT/m and 64/1000 mT/m, respectively. The Pearson’s correlation of mechanical property maps were determined voxel-wise between DTI-MRE and MRE in central slices.
For scans of performance comparison of experimental parameters, the voxel size, number of slices, matrix size, and TE are 3x3x3 mm³, 48, 80x80 and 80ms, respectively. 3D-dMRE without fractional encoding and DTI acquisitions without vibration were acquired for comparison with the DTI-MRE acquisition. Diffusion property maps and the complex shear modulus G* were calculated as previously described.² The Pearson’s correlation was determined voxel-wise between DTI-MRE and conventional methods in white matter of central slices.

Results

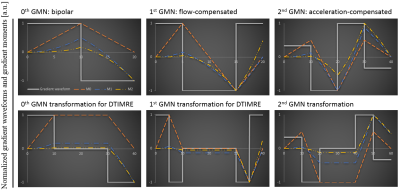
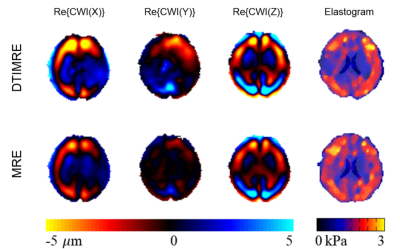
The gradient amplitude and the k-th gradient moment from GMN simulation were normalized for display in Figure 1. Of note, splitting of the gradient waveforms as required in DTI-MRE has impact on the 2^nd GMN characteristics compared to continuous gradient waveforms, while the 0^th and 1^st order characteristics are not affected. The Pearson’s correlation coefficients between DTI-MRE and conventional MRE with flow compensation for 8 central brain slices of the complex wave images (real parts) in 3 principle axes (Re{CWI(X)}, Re{CWI(Y)}, Re{CWI(Z)}) and the shear modulus (|G*|) maps (absolute value) were 0.91, 0.61, 0.98 and 0.74, respectively. The property maps of one central slice were displayed in Figure 2. The optimization of experimental parameters with 0^th GMN transformation identified 29 sets, as shown in the Table 1. No parameter set with 1^st GMN transformation was found that provide adequate diffusion timing. The obtained maximum b-value using 1^st GMN transformation at 50 Hz and gradient amplitude of 80 mT/m was 76.3 s/mm². The Good and Moderate sets from Table 1 were selected and listed in Table 2. The averaged Pearson’s correlation coefficients for Good (Moderate) parameter sets between DTI-MRE and conventional MRE / DTI in white matter of 4 central brain slices of 5 volunteers in mean diffusivity (MD), factional anisotropy (FA), Re{CWI(X)}, Re{CWI(Y)}, Re{CWI(Z)}, and |G*| maps were 0.78 (0.84), 0.93 (0.95), 0.86 (0.79), 0.60 (0.59), 0.77 (0.65) and 0.33 (0.31), respectively. A direct comparison of reconstructed MRE and DTI parameter maps with DTI-MRE from one volunteer is shown in Figure 3.

Discussion

Our preliminary results suggest that the simulations provide DTI-MRE experimental parameters optimized for best performance of the new technique. A good correlation between DTI-MRE and conventional measurements was found using either Good or Moderate parameter settings. Use of flow-compensated gradients in DTI-MRE works in theory but has a limit of not being able to reach high diffusion weighting. Nevertheless, similar complex wave images and stiffness maps are obtained after processing using (non-flow compensated) monopolar gradient waveforms in DTI-MRE and flow-compensated gradients in conventional MRE. We will conduct a study with a larger sample size in the next months to confirm these observations. DTI-MRE has the potential to increase the clinical acceptance of MRE and DTI by providing fast acquisitions and tissue mechanical and diffusion property maps that are immediately co-registered.

Acknowledgements

This work was supported by the NIH NIBIB under grant R21EB026238, Adding MRE to DTI for free. The work represents the views of the authors and not of the NIH.