3918
Brain Growth and Folding Processes Using Deep Neural Networks1Computer Science, State University of New York at Binghamton, Binghamton, NY, United States, 2Mechanical Engineering, State University of New York at Binghamton, Binghamton, NY, United States
Synopsis
Finite Element (FE)-based mechanical models can simulate the brain growth and folding process. But they are time consuming due to the large number of nodes in a real human brain and the reverse process to the initial smooth brain surfaces is difficult because it is not invertible problem. Here, we demonstrate a proof-of-concept that deep-learning neural networks (DNN) can learn the growth and folding process of human brain in forward and reverse directions and can predict/retrieve the developed/primary folding patterns in a very fast speed.
Introduction
The evolvement of human brain, which is also known as the cortical folding development, mainly happens during the gestation period [1, 2]. During this process, primary folding patterns (i.e., initial smooth fetal brain surfaces) of the fetal brain are developed into complex folding patterns [3], known as gyri and sulci. In the meanwhile, lots of cognitive or physiological impairments, e.g., lissencephaly, polymicrogyria, and autism, are believed to be the consequences of abnormal cortical folding during this early stage [4-6]. Therefore, the knowledge of the process from the primary folding patterns to developed folding patterns or even the reverse process for potential early diagnosis is of critical need. Finite element (FE)-based mechanical models based on differential tangential growth theory (differential growth rates from gray matter and white matter regions) have demonstrated their success in simulating growth and folding process in simple bilayer brain models [7-9]. However, these FE models are time consuming due to the large number of nodes in a real human brain and it cannot be directly inverted to mimic the reverse process from the complex folding patterns back to the primary folding patterns without constraining conditions. Here, we demonstrated a proof-of-concept that deep neural networks (DNN) can learn the growth and folding process of human brain in forward and reverse directions and can predict/retrieve the developed/primary folding patterns in a very fast speed (e.g., in seconds).Method
First, A 3D cuboid FE model was created as a small part of the brain. The model was divided into two layers: a thin layer of gray matter on a substrate as the white matter. According to the differential tangential growth concept, the gray matter grows on the white matter and forms folds. The initial smoothed brain surfaces (initial shapes) were generated on a regular (151, 151) square grid. Random Gaussian distributions with various amplitudes were used to simulate initial brain shapes. One FE model with the same parameters was applied to 986 initial shapes to generate corresponding 986 developed brain folding surfaces (final shapes). Each shape is represented by 22801 points (each point is denoted by its x, y and z coordinates) and there is a one-to-one correspondence for the points between the initial shape and final shape. Since the initial shape was sampled on a regular (151, 151) grid, we reorganized each shape into the 2D grid with the matrix size as (151, 151, 3). Because the FE model is rotation and flip invariant, the augmentations (rotating 90, rotating 180, rotating 270, flip x-axis and flip y-axis) were applied to each shape pair to enhance the size of the training dataset, and hence the total number of pairs are 5916.Next, we built the conditional generative adversarial network (cGAN, Fig.1) to learn the brain growth and folding from initial shapes to final shapes. The generator (Fig.1 Left) for the cGAN is a U-Net based 2D convolutional neural network (CNN) with skip connection between the corresponding layers in encoder and decoder. The discriminator (Fig. 1 Right) for the cGAN is a CNN with binary output to distinguish the fake and real input pairs. The input and target shapes for the generator are initial shapes and corresponding final shapes, respectively. The input shapes for the discriminator are the final shape and output shape from the generator. 5496 pairs of initial shapes and final shapes were used in the training of cGAN. After two hundreds epochs of training, we used the derived generator to predict the final shape on the testing dataset. In addition, we also used the same cGAN network to evaluate its performance on retrieving the initial shape from the final shape by training a separate network with the final shape as input and initial shape as the target. The performance of cGAN was evaluated by calculating the mean squared error (MSE), peak signal-to-noise ratio (PSNR) and Structural Similarity Index (SSIM) of generated shapes by comparing with their corresponding ground-truth shapes.
Results & Discussion
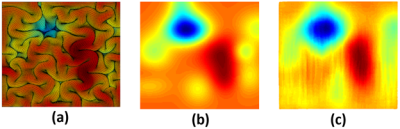
For the forward process, the predicted final shape (Fig. 2c) from the input initial shape (Fig. 2a) and the ground-truth final shape (Fig. 2b) shared similar folding patterns. For the reverse process, the retrieved initial shape (Fig. 3c) from the input final shape (Fig. 3a) and the ground-truth initial shape (Fig. 3b), had similar smoothed folding patterns. The quantitative metrics in Table 1 confirmed the markedly improved similarity to the output brain shapes than to the input brain shapes (compared to the ground-truth shapes). It is worth noting that the reverse cGAN has minimal MSE and maximal SSIM, indicating the smooth brain is much easier to learn using DNN although the reverse process is not an invertible problem. The results demonstrate that both forward and reverse cGANs can learn the forward or backward processes of brain growth and folding successfully.Conclusion
cGAN, a DNN model, is promising in predicting the brain developed folding pattern from the initial smooth folding pattern or retrieving the initial smooth folding pattern from the developed folding pattern. Further studies will focus on directly applying the DNN on an irregular 3D geometric grid from real fetal MRI to learn the 3D brain folding process.Acknowledgements
No acknowledgement found.References
1. Encinas, J.L., et al., Maldevelopment of the cerebral cortex in the surgically induced model of myelomeningocele: implications for fetal neurosurgery. J Pediatr Surg, 2011. 46(4): p. 713-722.2. Sun, T. and R.F. Hevner, Growth and folding of the mammalian cerebral cortex: from molecules to malformations. Nat Rev Neurosci, 2014. 15(4): p. 217-32.
3. Garcia, K.E., et al., Dynamic patterns of cortical expansion during folding of the preterm human brain. Proc Natl Acad Sci U S A, 2018. 115(12): p. 3156-3161.
4. Nordahl, C.W., et al., Cortical folding abnormalities in autism revealed by surface-based morphometry. J Neurosci, 2007. 27(43): p. 11725-35.
5. Palaniyappan, L., et al., Folding of the prefrontal cortex in schizophrenia: regional differences in gyrification. Biol Psychiatry, 2011. 69(10): p. 974-9.
6. Voets, N.L., et al., Increased temporolimbic cortical folding complexity in temporal lobe epilepsy. Neurology, 2011. 76(2): p. 138-44.
7. Razavi, M.J., et al., Radial Structure Scaffolds Convolution Patterns of Developing Cerebral Cortex. Front Comput Neurosci, 2017. 11: p. 76.
8. Razavi, M.J., et al., Role of mechanical factors in cortical folding development. Phys Rev E Stat Nonlin Soft Matter Phys, 2015. 92(3): p. 032701.
9. Razavi, M.J., et al., Cortical Folding Pattern and its Consistency Induced by Biological Growth. Sci Rep, 2015. 5: p. 14477.
Figures
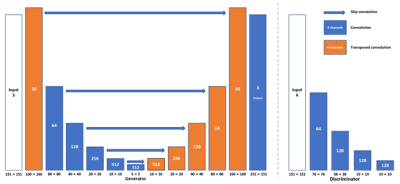
Figure 1. (Left) Network architecture of generator. (Right) Network architecture of discriminator. Each convolution layer contains convolution (Conv2D), batch normalization (BN) and Leaky version of a Rectified Linear Unit (LeakyReLU). Each transposed convolution layer contains transposed convolution (Conv2DTranspose), BN and LeakyReLU. For both Conv2D and Conv2DTranspose, convolutional kernel size is 4. The value below the input represents the number of channels of the input image. The shape below each pillar shows the output shape from this layer.

Figure 2. The forward process of brain growth and folding. (a) Top view of cortex before growth (initial shape as input). (b) Top view of cortex after growth (final shape as ground-truth). (c) Estimated final shape using the forward cGAN.