3913
A comparison of model-based deconvolution methods for estimating the carbon-dioxide response function in resting-state fMRI1Rotman Research Institute, Baycrest, Toronto, ON, Canada, 2Gordon Center for Medical Imaging, Massachusetts General Hospital, Harvard Medical School, Boston, MA, United States, 3McGill University, Montreal, ON, Canada, 4Rotman Research Institute, Baycrest Health Sciences, Toronto, ON, Canada
Synopsis
The resting-state fMRI response to carbon-dioxide (CO2) fluctuations is useful for denoising and for physiological mapping. In this work, we compare model-based deconvolution methods for estimating this response function (CRF) in a wide range of signal-to-noise conditions and with various assumed ground-truth CRF shapes. We also propose an improved method using canonical correlation analysis to identify the optimal CRF adaptively. The best choice of method depends on the desired CRF parameter, such as timing (dynamics) or area (static cerebrovascular reactivity). The inverse-Logit and adaptive CCA methods provided the highest accuracy and robustness.
Introduction
The vascular contribution to resting-state fMRI (rs-fMRI) is increasingly recognized as a major non-neural confound 1, and modeling the fMRI response function to CO2 (CRF) can play a key role for physiological correction in resting-state functional-connectivity mapping. On the other hand, CO2 influence also presents a valuable opportunity to extract cerebrovascular reactivity (CVR), and the unique value of the CVR dynamics embodied in CRF is increasingly recognized 2. However, due to the low signal-to-noise (SNR) conditions in rs-fMRI, deconvolution of resting CO2 fluctuations from the fMRI signal is non-trivial. In such cases, model-based methods are generally more robust 3, but with the caveat that their performance may depend on the underlying model structure. In this work, we compare several model-based deconvolution techniques for capturing the characteristics of CRF, including: (1) the maximum a-posteriori (MAP) method using a Gaussian basis 4; (2) the inverse Logit (IL) method 5; (3) canonical correlation analysis (CCA) using a single-gamma function and its derivatives 6,7; (4) the basis expansion method using Gamma basis functions (VKG) 8, and (5) the basis expansion method with spherical Laguerre functions (VKL) 9. We further introduce a sixth method, an optimized CCA approach, which leverages the simplicity of the CCA method but allows for more flexibility in the employed basis sets. We directly compare these six methods under different ground-truth CRF assumptions and different SNR conditions to identify their suitability for estimating different aspects of CRF.Methods
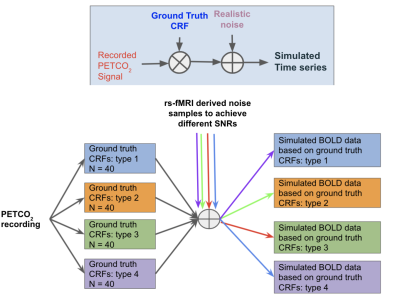
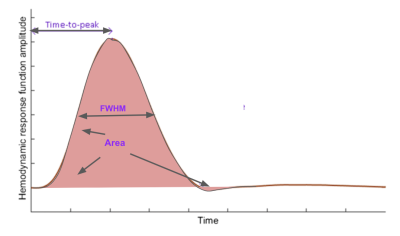
Similar to the original CCA method6,7, the proposed optimized CCA method maximizes the correlation between the fMRI signal and a linear combination of the convolved HRF subspaces to identify the optimal HRF, and capitalizes on the Taylor-series expansion of the Gamma function to allow for fine-tuning of the HRF. Unlike the original CCA method, the optimized CCA allows the parameters defining the Gamma basis to be updated iteratively to further improve the model fit. To comprehensively compare all methods, we adopted a simulation-based approach (Fig. 1) in which all methods were tested on data generated using one of four ground-truth HRF models: (1) single Gamma6,7; (2) double Gamma10; (3) inverse logit5, and (4) Gaussian11. Each assumed ground-truth model generated a set of possible HRFs based on physiologically and pathologically plausible parameter ranges. Each of these ground-truth HRFs was convolved with an experimentally measured resting-state end-tidal CO2 (PETCO2) time-course. To simulate different SNRs, we extracted experimental rs-fMRI time courses acquired on our Siemens TIM Trio 3 T scanner from a healthy young adult; these rs-fMRI signals were permuted to generate 1000 realizations of realistic noise, which were then added to the convolved signal to achieve SNRs between -10 and 6.9 dB 12 (with SNR of -10dB corresponding to a S/N ratio of 0.1). Note that in this case the CO2-driven fraction of the simulated rs-fMRI data is the “signal”, and everything else is “noise”. To evaluate different aspects of CRF estimation, we chose 4 quality metrics (Fig. 2): (1) HRF time to peak (TTP); (2) HRF full-width-at-half-maximum (FWHM); (3) HRF area (equivalent to CVR magnitude); (4) Pearson’s correlation between estimated and ground-truth HRF. The significance of differences between accuracy rates were compared across methods using pairwise t-tests.Results
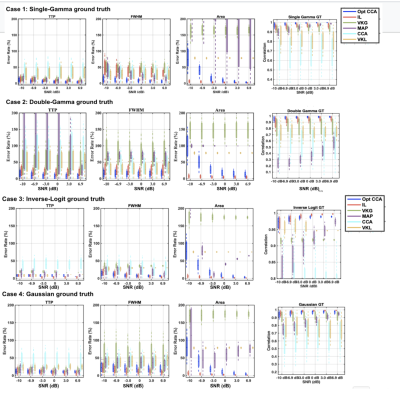
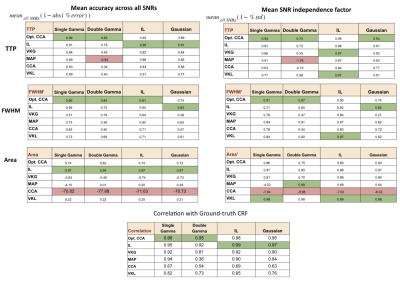
The performance of each method was assessed using the fractional estimation error of the 4 evaluation metrics, and are summarized in Fig. 3. Across all SNs, ground truths, and HRF metrics, the IL and optimized CCA methods generated the lowest error rates. However, for the IL method, optimal performance required parameter search by simulated annealing, thus making it 20 times slower than the optimized CCA method. These results are further summarized in Fig. 4, which assigns each method a score based not only on its mean accuracy but also on its SNR dependence. The methods with the highest accuracy and SNR independence are considered ideal.Discussion and conclusions
As expected, the performances of these model-based methods were ground-truth dependent, but to our surprise, the performance of the methods was not dictated by their underlying model-structure assumptions. The 2 leading methods are the IL method and the proposed optimized CCA method. The newly proposed optimized CCA method overcoming the limitations of the conventional CCA method, being the leading method for estimating the timing of the HRF (TTP and FWHM). On the other hand, the IL method is best for estimating the CVR amplitude (area of HRF). The VKL and VKG methods, conversely, displayed considerable SNR dependence.In this study, we demonstrate that it is possible to obtain accurate CRF estimates using model-based deconvolution even in extremely low SNR conditions. It is likely that the choice of method between the optimized CCA and IL methods will depend on the HRF metric of interest and limitations in computational resources.
Acknowledgements
We thank the Canadian Institutes of Health Research and the Natural Sciences and Engineering Research Council for their financial support.References
1. Golestani, A. M., Kwinta, J. B., Strother, S. C., Khatamian, Y. B. & Chen, J. J. The association between cerebrovascular reactivity and resting-state fMRI functional connectivity in healthy adults: The influence of basal carbon dioxide. Neuroimage 132, 301–313 (2016).
2. Duffin, J. et al. The dynamics of cerebrovascular reactivity shown with transfer function analysis. Neuroimage 114, 207–216 (2015).
3. Chen, J. J., Smith, M. R. & Frayne, R. Advantages of frequency-domain modeling in dynamic-susceptibility contrast magnetic resonance cerebral blood flow quantification. Magn. Reson. Med. 53, 700–707 (2005).
4. Chang, C., Cunningham, J. P. & Glover, G. H. Influence of heart rate on the BOLD signal: the cardiac response function. Neuroimage 44, 857–869 (2009).
5. Lindquist, M. & Wager, T. Modeling the hemodynamic response function using inverse logit functions. in Proceedings of the Human Brain Mapping Annual Meeting (2005).
6. Hossein-Zadeh, G.-A., Ardekani, B. A. & Soltanian-Zadeh, H. Activation detection in fMRI using a maximum energy ratio statistic obtained by adaptive spatial filtering. IEEE Trans. Med. Imaging 22, 795–805 (2003).
7. Shams, S.-M., Hossein-Zadeh, G.-A. & Soltanian-Zadeh, H. Multisubject activation detection in fMRI by testing correlation of data with a signal subspace. Magn. Reson. Imaging 24, 775–784 (2006).
8. Prokopiou, P. C., Pattinson, K. T. S., Wise, R. G. & Mitsis, G. D. Modeling of dynamic cerebrovascular reactivity to spontaneous and externally induced CO2 fluctuations in the human brain using BOLD-fMRI. Neuroimage 186, 533–548 (2019).
9. Prokopiou, P. C., Xifra-Porxas, A. & Kassinopoulos, M. Modeling the hemodynamic response function using motor task and eyes-open resting-state EEG-fMRI. bioRxiv (2020).
10. Li, M., Newton, A. T., Anderson, A. W., Ding, Z. & Gore, J. C. Characterization of the hemodynamic response function in white matter tracts for event-related fMRI. Nature Communications vol. 10 (2019).
11. Goutte, C., Nielsen, F. A. & Hansen, L. K. Modeling the haemodynamic response in fMRI using smooth FIR filters. IEEE Trans. Med. Imaging 19, 1188–1201 (2000).
12. Golestani, A. M., Wei, L. L. & Chen, J. J. Quantitative mapping of cerebrovascular reactivity using resting-state BOLD fMRI: Validation in healthy adults. Neuroimage 138, 147–163 (2016).
Figures