3900

Unbiasing orientationally-averaged diffusion MRI signal
Tomasz Pieciak1, Maryam Afzali2,3, Antonio Tristán-Vega1, and Santiago Aja-Fernández1
1Laboratorio de Procesado de Imagen (LPI), Universidad de Valladolid, Valladolid, Spain, 2Leeds Institute of Cardiovascular and Metabolic Medicine, University of Leeds, Leeds, United Kingdom, 3Cardiff University Brain Research Imaging Centre (CUBRIC), School of Psychology, Cardiff University, Cardiff, United Kingdom

Synopsis

The orientationally-averaging or the so-called power-averaging is a common approach to reduce the impact of macroscopic anisotropy in diffusion MRI (dMRI). This paper analytically derives two new closed-form unbiased orientationally-averaging diffusion MRI signal estimators and shows that the noise-related bias could be significantly suppressed with these new findings. The new formulas might be applied to retrospectively orientationally-averaged dMRI signals with minimal computational effort.

Introduction

The orientationally-averaging is a common approach used to reduce the impact of macroscopic anisotropy in diffusion MRI (dMRI)1,2,3,4. The orientationally-averaged dMRI signals have been successfully practised in tissue characterization, including estimation of the diffusivities parallel and perpendicular to axon13, the T2 relaxation time of intra‐axonal water14 and free-water fraction volume16, white matter segmentation17, or as regularization priors for kurtosis estimation18. The orientationally-averaged signal is typically calculated as the average of diffusion-weighted signal over the samples in the $$$\mathbf{q}$$$-space domain, driving to unwanted noise-induced bias due to a positive skewness of Rician distribution, being de facto the standard statistics used in dMRI6,7. This paper analytically proposes two new closed-form unbiased orientationally-averaging dMRI signal estimators and shows that the noise-related bias could be significantly suppressed. The new formulas might be applied to a retrospectively orientationally-averaged dMRI with minimal computational effort.

Methods and materials

The orientationally-averaged signal: The orientationally-averaged diffusion-weighted MRI signal can be calculated as the weighted mean over the $$$\mathbf{q}$$$-space domain samples 2,3,4,14
$$\overline{S}(b)=\sum_{i=1}^{N_g}w_i S(\mathbf{g}_i, b),\ \ \ 0\le w_i\le 1$$
with $$$S(\mathbf{g}_i, b)$$$ being the sample acquired in $$$i$$$-th gradient direction at a specific $$$b$$$-value, and $$$N_g$$$ being the total number of gradient directions defined over the shell $$$b$$$, and $w_i$ is the normalized weight used to compensate the non-uniformity of gradients distribution over the sphere, or via the spherical harmonics (SH) decomposition of the signal2,15
$$\overline{S}(b)=C_{00}\left\{S(\mathbf{g},b)\right\}=\frac{1}{\sqrt{4\pi}}\int_{S}S(\mathbf{g},b) d \mathbf{g}$$
where $$$C_{00}\left\{S(\mathbf{g},b)\right\}$$$ is the zeroth-order SH decomposition of the signal, or alternatively using the Mean Apparent Propagator MRI coefficients2,5.

Unbiasing orientationally-averaged signal: Calculating the orientationally-averaged signal might introduce a noise-related bias due to a positively-skewed Rician distribution being a typical statistical model assumed in dMRI6, 7,13. Assuming the samples $$$\left\{S(\mathbf{g}_i,b)\right\}_{i=1}^{N_g}$$$ are independent and non-identically Rician distributed, i.e. $$$S(\mathbf{g}_i,b)\sim \mathrm{Rice}(A(\mathbf{g}_i, b),\sigma(b))$$$ with the noise-free amplitude $$$A(\mathbf{g}_i,b)$$$ and non-centrality parameter $$$\sigma(b)$$$ defined for each $$$b$$$-value independently, we can define the asymptotic expansion of the expectation operator of the signal8, $$$\mathbb{E}\{S(\mathbf{g},b)\}=\sigma(b)\sqrt{2x}+\frac{1}{2}\sqrt{\frac{2}{x}}+\mathcal{O}\left(x^{-3/2}\right)$$$ with $$$x=\frac{A^2(\mathbf{g}, b)}{2\sigma^2(b)}$$$ and $$$\mathcal{O}(\cdot)$$$ being the decay of the corresponding term as fast as the function argument. Starting from give asymptotic expansion of the expectation operator, we analytically derive two new unbiased orientationally-averaged diffusion-weighted MRI signal estimators:

$$\overline{S}_{\mathrm{unbiased}}^{(1)}(b)=\sum_{i=1}^{N_g}w_iS(\mathbf{g}_i,b)-\frac{1}{2}\widehat{\sigma}^2(b) \left( \sum_{i=1}^{N_g}w_i S(\mathbf{g}_i,b)\right)^{-1}=\overline{S}(b)-\frac{1}{2} \frac{\sigma^2(b)}{\overline{S}(b)}$$

$$\overline{S}_{\mathrm{unbiased}}^{(2)}(b)=\frac{1}{2} \left(\sum_{i=1}^{N_g}w_iS(\mathbf{g}_i,b)+\left(\sum_{i=1}^{N_g}w_i S(\mathbf{g}_i,b)-\sqrt{2}\sigma(b)\right)^{1/2} \left(\sum_{i=1}^{N_g}w_i S(\mathbf{g}_i,b)+\sqrt{2}\sigma(b)\right )^{1/2}\right) \\
= \frac{1}{2} \left( \overline{S}(b) + \left( \overline{S}(b) - \sqrt{2}\sigma(b) \right )^{1/2} \left( \overline{S}(b) + \sqrt{2}\sigma(b) \right )^{1/2} \right)$$

where $$$\sigma(b)$$$ is the noise level measured in a voxel-wise manner under a specific $$$b$$$-value. The parameter $$$\sigma(b)$$$ can be estimated from all samples available in a voxel, i.e. $$$\widehat{\sigma}(b) = \varphi(\left\{S(\mathbf{g}_1),\ldots,S(\mathbf{g}_{N})\right\})$$$ with $$$\varphi(\cdot)$$$ being the operator used to obtain the noise level (e.g. median absolute deviation9, random matrix theory based method10) or taking into account a spatial neighbourhood of the sample11,12.

In silico data: The synthetic dMRI signal was generated under three scenarios: 1) free-water diffusion with a fixed diffusivity at $$$D_0=3.0\times10^{-3}\ \mathrm{mm}^2/\mathrm{s}$$$, 2) restricted diffusion with parallel and perpendicular diffusivities at $$$D_{||}=2.0\times10^{-3}\ \mathrm{mm}^2/\mathrm{s}$$$ and $$$D_\perp=0.75\times10^{-3}\ \mathrm{mm}^2/\mathrm{s}$$$, and 3) a mixture of free-water and restricted diffusion with a volume fraction of $$$f=0.2$$$ and same parallel and perpendicular diffusivities. All signals were generated under $$$b=1000\ \mathrm{s}/\mathrm{mm}^2$$$ and 90 uniformly distributed gradient directions.

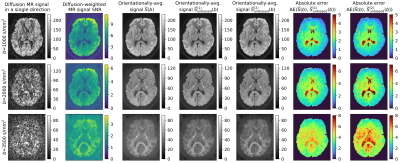
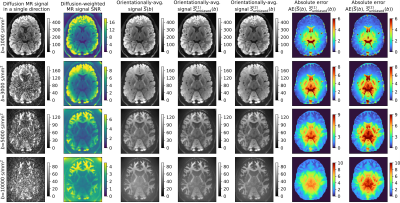
In vivo data: We use two publicly available datasets: 1) Sherbrooke diffusion MRI data acquired with a 1.5T Siemens scanner and delivered with DIPY tool19. The data consists of three shells at $$$(1000,2000,3500)\ \mathrm{s}/\mathrm{mm}^2$$$ and 64 gradient directions per a single shell, and 2) the Human Connectome Project (HCP) MGH20 data (subject 1016) acquired on a Siemens 3T Connectom scanner at four b-values $$$(1000,3000,5000,10000) \ \mathrm{s}/\mathrm{mm}^2$$$ with $$$(64,64,128,256)$$$ gradient directions, voxel resolution of $$$1.5 \ \mathrm{mm}^3$$$.

Data processing: To estimate the parameter $$$\sigma(b)$$$, we use a variance-stabilizing homomorphic filter11,12 applied over each gradient direction and aggregate them to a representative noise level using a mean operator across all gradient directions at the specified $$$b$$$. Orientationally-averaged signals are calculated using the SH expansion at the order of 2.

Results

  • Fig.1 displays the relative error (in %) and Fig.2 shows the bias of the orientationally-averaged dMRI signal obtained with three estimators, namely the standard one and two proposed under three scenarios: 1) free-water diffusion, 2) restricted diffusion and 3) combined diffusion with a free-water volume fraction of $$$f=0.2$$$.
  • Fig.3 and Fig.4 visually inspects the orientationally-averaged dMRI signals in axial slices using two in vivo datasets with the estimators specified above, along with the absolute errors calculated between the standard approach and unbiased equivalents.

Discussion and conclusions

In this paper, we analytically derived two new unbiased orientationally-averaging estimators under the assumption of Rician statistics for dMRI data. Our study has led to the following conclusions:
  1. Proposed estimators significantly reduce the orientationally-averaging noise-induced bias due to aggregation of the samples from positive skewed Rician statistics.
  2. Under the high SNR of the dMRI data, i.e. $$$\widehat{\sigma}(b) \rightarrow 0$$$, the correction components in both estimators $$$\overline{S}_{\mathrm{unbiased}}^{(1)}(b)$$$ and $$$\overline{S}_{\mathrm{unbiased}}^{(2)}(b)$$$ rule out themselves, and consequently, the equations reduce to the standard formula.
  3. New signal estimators are easy to obtain directly or via the SH expansion, can be applied to retrospectively orientationally-averaged dMRI signals, and do not require any non-standard tools or algorithms to be used except for the noise level estimation.

Acknowledgements

The authors acknowledge Ministerio de Ciencia e Innovación of Spain with research grant RTI2018-094569-B-I00. Tomasz Pieciak acknowledges the Polish National Agency for Academic Exchange for the grant PN/BEK/2019/1/00421 under the Bekker programme and the Ministry of Science and Higher Education (Poland) under the scholarship for outstanding young scientists. Maryam Afzali acknowledges a Wellcome Trust Investigator Award (219536/Z/19/Z).

References

  1. Callaghan, P. T., & Soderman, O. (1983). Examination of the lamellar phase of aerosol OT/water using pulsed field gradient nuclear magnetic resonance. The Journal of Physical Chemistry, 87(10), 1737-1744.
  2. Afzali, M., Knutsson, H., Özarslan, E., & Jones, D. K. (2021). Computing the orientational-average of diffusion-weighted MRI signals: A comparison of different techniques. Scientific Reports, 11(1), 1-16.
  3. Afzali, M., Aja-Fernández, S., & Jones, D. K. (2020). Direction-averaged diffusion-weighted MRI signal using different axisymmetric B-tensor encoding schemes. Magnetic resonance in medicine, 84(3), 1579-1591.
  4. Herberthson, M., Yolcu, C., Knutsson, H., Westin, C. F., & Özarslan, E. (2019). Orientationally-averaged diffusion-attenuated magnetic resonance signal for locally-anisotropic diffusion. Scientific reports, 9(1), 1-12.
  5. Özarslan, E., Koay, C. G., Shepherd, T. M., Komlosh, M. E., İrfanoğlu, M. O., Pierpaoli, C., & Basser, P. J. (2013). Mean apparent propagator (MAP) MRI: a novel diffusion imaging method for mapping tissue microstructure. NeuroImage, 78, 16-32.
  6. Gudbjartsson, H., & Patz, S. (1995). The Rician distribution of noisy MRI data. Magnetic resonance in medicine, 34(6), 910-914.
  7. Aja-Fernández, S., & Vegas-Sánchez-Ferrero, G. (2016). Statistical analysis of noise in MRI. Switzerland: Springer International Publishing.
  8. Pieciak, T., Rabanillo-Viloria, I., & Aja-Fernández, S. (2018, April). Bias correction for non-stationary noise filtering in MRI. In 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018) (pp. 307-310). IEEE.
  9. Maximov, I. I., Farrher, E., Grinberg, F., & Shah, N. J. (2012). Spatially variable Rician noise in magnetic resonance imaging. Medical image analysis, 16(2), 536-548.
  10. Veraart, J., Fieremans, E., & Novikov, D. S. (2016). Diffusion MRI noise mapping using random matrix theory. Magnetic resonance in medicine, 76(5), 1582-1593.
  11. Pieciak, T., Aja-Fernandez, S., & Vegas-Sanchez-Ferrero, G. (2017). Non-stationary Rician noise estimation in parallel MRI using a single image: a variance-stabilizing approach. IEEE transactions on pattern analysis and machine intelligence, 39(10), 2015-2029.
  12. Aja-Fernandez, S., Pieciak, T., & Vegas-Sánchez-Ferrero, G. (2015). Spatially variant noise estimation in MRI: A homomorphic approach. Medical image analysis, 20(1), 184-197.
  13. Kaden, E., Kelm, N. D., Carson, R. P., Does, M. D., & Alexander, D. C. (2016). Multi-compartment microscopic diffusion imaging. NeuroImage, 139, 346-359.
  14. McKinnon, E. T., & Jensen, J. H. (2019). Measuring intra‐axonal T2 in white matter with direction‐averaged diffusion MRI. Magnetic resonance in medicine, 81(5), 2985-2994.
  15. Descoteaux, M., Angelino, E., Fitzgibbons, S., & Deriche, R. (2007). Regularized, fast, and robust analytical Q‐ball imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 58(3), 497-510.
  16. Tristán-Vega, A., París, G., de Luis‐García, R., & Aja-Fernández, S. (2021). Accurate free-water estimation in white matter from fast diffusion MRI acquisitions using the spherical means technique. Magnetic Resonance in Medicine.
  17. Cheng, H., Newman, S., Afzali, M., Fadnavis, S. S., & Garyfallidis, E. (2020). Segmentation of the brain using direction-averaged signal of DWI images. Magnetic resonance imaging, 69, 1-7.
  18. Henriques, R. N., Jespersen, S. N., Jones, D. K., & Veraart, J. (2021). Toward more robust and reproducible diffusion kurtosis imaging. Magnetic Resonance in Medicine.
  19. Garyfallidis E, Brett M, Amirbekian B, Rokem A, van der Walt S, Descoteaux M, Nimmo-Smith I and Dipy Contributors (2014). DIPY, a library for the analysis of diffusion MRI data. Frontiers in Neuroinformatics, vol.8, no.8.
  20. Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E., Yacoub, E., Ugurbil, K., & Wu-Minn HCP Consortium. (2013). The WU-Minn human connectome project: an overview. Neuroimage, 80, 62-79.

Figures

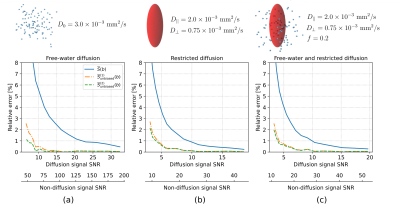
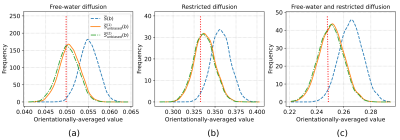
Fig. 1 In silico experiment presenting the changes in the relative error (given in %) of three estimators for the orientationally-averaged dMRI signal under three scenarios: (a) free, (b) restricted, and (c) free-water and restricted diffusion, all under $$$b=1000 \ \mathrm{s}/\mathrm{mm}^2$$$. Each characteristic is presented in two variants, as a function of 1) diffusion-weighted signal SNR and 2) non-diffusion-weighted signal SNR (i.e., baseline SNR calculated at $$$b=0$$$). In total, over 500 repetitions were conducted for each SNR level.

Fig. 2 Histograms of the orientationally-averaged synthetic dMRI signals obtained with standard and unbiased estimators under fixed SNR levels and three scenarios: (a) free, (b) restricted, and (c) free-water and restricted diffusion, all under $$$b=1000 \ \mathrm{s}/\mathrm{mm}^2$$$. The red dotted line in each case presents the ground-truth value of the normalized dMRI signal. The SNRs given for diffusion-weighted signals: (a) 2.24, (b) 2.02 and (c) 2.07. The histograms were generated from 5000 samples (experiment repetitions).


Fig. 3 Orientationally-averaged diffusion-weighted MR signals (Sherbrooke data, slice 28) estimated with a standard method and new unbiased solutions, all evaluated under three b-values. The last two columns present the absolute errors between the standard approach and the proposed unbiased equivalents. The estimated SNRs of diffusion-weighted dMRI signals (from the lowest to highest b-value): 6.47, 3.61 and 2.4.

Fig. 4 Orientationally-averaged diffusion-weighted MR signals (HCP MGH, subject 1016, slice 42) estimated with a standard method and new unbiased solutions, all evaluated under three b-values. The last two columns present the absolute errors between the standard approach and the proposed unbiased equivalents. The estimated SNRs of diffusion-weighted signals (from the lowest to highest b-value): 10.17, 5.21, 3.62, 2.78.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
3900
DOI: https://doi.org/10.58530/2022/3900