3876
Estimation of axon-bundle parallel-diffusivity on clinical settings with linear-encoding DW-MR data1Computer Science, Centro de Investigación en Matemáticas A.C., Guanajuato, Mexico, 2Department of Chemical, Electronic and Biomedical Engineering, Division of Sciences and Engineering, University of Guanajuato, Guanajuato, Mexico, Leon, Mexico, 3Institute of Neurobiology, Universidad Nacional Autonoma de Mexico, Juriquilla, Mexico
Synopsis
The estimation of reliable parameters of multi-compartment models of water diffusivity is a challenging open problem, especially when low-SNR clinical-datasets are analyzed. The ill-posedness of the models requires fixing a subset of parameters in order to estimate the rest of them. We propose a simple and fast method where only averaged parameters are required (not voxelwise information is required). The method is based on the processing of powder-averaged data to estimate a robust value for the axon-bundle parallel-diffusivity. We test the robustness of the method on synthetic experiments and show the results on in-vivo human and ex-vivo rodent datasets.
Introduction
Multicompartment models are widely used to estimate brain tissue parameters1, however, the model fitting may result in degenerated solutions2. Recent works provide approximate values for the multi-compartment parameters by using modern acquisition protocols3,4 , however, it is still required to estimate them on linear-encoding data acquired in clinical settings with low SNR, as for instance in the HCP datasets. In this work we focus on the estimation of the parallel-diffusivity, $$$d_{||}$$$, in microenvironments composed of axon-packages and their extracellular surroundings. The method is simple and only averaged estimations of intracellular signal fraction (ICSF) values are required. The main assumption of this work is that this value is almost the same for all white matter voxels. Once $$$d_{||}$$$ is estimated, it can be fixed, eliminating in this way the degeneration on the estimation of the rest of the parameters. The robust estimation of $$$d_{||}$$$ is important as several methods required it as input, as for instance5,6 and the method developed by our group in7, such that other useful parameters can be voxel-wise computed, such as the ICSF and axonal dispersion. We show that by introducing an approximate value of the averaged ICSF in the analysis one can reliably estimate $$$d_{||}$$$ values.Methods
Based on the assumption that $$$d_{||}$$$ is almost constant inside the white matter, our methodology is composed of the following stages:1. Manual selection of the white matter voxels to be analyzed, Figure 1a and 1b.
2. Simplification of the estimation problem by the voxelwise computation of the Spherical Mean signature8 of the DW signal, $$$SM_v$$$, i.e. factoring out the axonal dispersion.
3. Computation of the averaged $$$SM$$$ for all the voxels, denoted as $$$\bar{SM} = \sum_v SM_v$$$.
On ex vivo data:
4. Set the multicompartment model to be fitted
$$\bar{SM} \approx \bar{f}_{ic} SM_{ic}(d_{||}) + \left(1-\bar{f}_{ic} - \bar{f}_{free} - \bar{f}_{dot} \right) SM_{zep}(d_{||}, \bar{f}_{ic}) + \bar{f}_{free} SM_{free} + \bar{f}_{dot} SM_{dot}$$
where $$$\bar{f}_{ic} = sum_v f^{v}_{ic}$$$ and $$$\bar{f}_{free}$$$ are the averaged ICSF and average free diffusivity size compartment, respectively, both are estimated from histology, see Figure 1c. $$$\bar{f}_{dot}$$$ is the dot averaged size compartment and is fixed equal to 1% according to4. $$$SM_{ic}(d_{||})$$$ and $$$SM_{zep}(d_{||}, \bar{f}_{ic})$$$ are computed from stick and zeppelin models1 with the tortuosity model in5.
5. Perform a discrete search for the $$$d_{||}$$$ (step size = 0.005e-9 m2/s) that minimizes the L2 norm between the multi-compartment model in step 4. and $$$\bar{SM}$$$.
On in vivo data (no histology is available):
6. Select an approximate plausible value for $$$\bar{f}_{ic}$$$ in the range of observed values: $$$\bar{f}_{ic}$$$ = (0.5+0.85)/2 = 0.675
7. Set the multicompartment model to be fitted as:
$$\bar{SM} \approx \bar{f}_{ic} SM_{ic}(d_{||}) + (1-\bar{f}_{ic} ) SM_{zep}(d_{||}, \bar{f}_{ic})$$
8. Perform a discrete search for the $$$d_{||}$$$ that minimizes the L2 norm between the multi-compartment model in step 7. and $$$\bar{SM}$$$.
Experiments and Results
The in-vivo human dataset includes 5 subjects (MGH_1007,MGH_1010,MGH_1016,MGH_1019,MGH_1031) from the HCP9 dataset (30 S0 images, 5 shells b=[1000,2000,3000,5000,10000]), SNR = 12. For the ex-vivo rodent data we process D-MR data from 8 healthy rats (30 S0 images, 5 shells b=[1000,2000,3000,5000,10000]) , SNR = 18 (after denoising10). The proposal is evaluated on multicompartment synthetic signals generated from different distributions of the voxel-wise $$$f_{ic}$$$ values in the interval [0.5,0.85], as shown in Figure 2. Figure 3 shows the results for the synthetic data that corresponds to the in-vivo HCP acquisition, we compare the performance of our proposal (steps 1-2-3-6-7-8 in Methods) vs. a free complete search were $$$\bar{f}_{ic}$$$ is also estimated, and when the estimation of $$$d_{||}$$$ is performed by the methodology in8. Figure 4 shows the results as in Figure 3, but for the synthetic data that corresponds to the rodent ex-vivo acquisition (steps 1-2-3-4-5 in Methods). The analysis of the histology of the rat nerves, Figure 1c, give us the estimation $$$\bar{f}_{ic} = 0.674$$$. Finally, Figure 5 show the plots of the estimation of $$$d_{||}$$$ on the real in-vivo and ex-vivo datasets.Discussion
The proposal allows estimating a good quality value for $$$d_{||}$$$ on low-SNR data. On the contrary, for high SNR data the complete search, including $$$\bar{f}_{ic}$$$ parameter, presents better results. Our experiments indicate that the use of SMT in8 on low SNR data, as well as when multiple compartments coexist within the voxel results in a poor estimation of the $$$d_{||}$$$ value. The synthetic experiments reproduce the degeneration problems in model fitting for in-vivo and ex-vivo cases e.g. when the $$$\bar{f}_{ic}$$$-free search is executed on highly noisy data, the estimated ICSFs are saturated. On the contrary, Figure 5 shows that the estimators provided by the proposal are plausible: the $$$\bar{f}_{ic}$$$ are not implausibly saturated close to 1 and the $$$d_{||}$$$ values are larger than the DT axial diffusivity, as expected.Figure 5, shows that the averaged $$$d_{||}$$$ value with our proposal for the in vivo dataset is 1.63e-9m2/s and for the ex vivo rat dataset is equal to 0.436e-9m2/s (green horizontal lines).
Conclusions
The simple introduction of plausible ICSF averaged-value allows estimating useful $$$d_{||}$$$ values on low-SNR linear encoding DW-MR data. The methodology can be applied to the analysis of challenging ex-vivo experiments as well as on in vivo human data.Acknowledgements
ARM was partially supported by CONACyT-Mexico.References
1. Uran Ferizi, Torben Schneider et al. White matter compartment models for in vivo diffusion MRI at 300 mT/m. Neuroimage, 2015. 118(1). 468-483
2. Ileana O. Jelescu, Jelle Veraart et al. Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue. NMR Biomed. 2016. 29(1). 33–47.
3. Bibek Dhita, Marco Reisert et al. Intra-axonal diffusivity in brain white matter. NeuroImage. 2019. Volume 189(1). 543-550.
4. Chantal M.W. Tax, Filip Szczepankiewicz, et al. The dot-compartment revealed? Diffusion MRI with ultra-strong gradients and spherical tensor encoding in the living human brain. NeuroImage. 2020. 210(1). 1-14.
5. Hui Zhang, T. Schneider et al. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage.2012. 61(4):1000-1016
6. A. Daducci and A. Dal Palu et al. COMMIT: Convex Optimization Modeling for Micro-structure Informed Tractography. IEEE Trans. on Med. Imag. 2015. 34(1):246-57
7. Uran Ferizi, Benoit Scherrer, Torben Schneider et al. Diffusion MRI microstructure models with in vivo human brain Connectome data: results from a multi-group comparison. NMR in Biomedicine. 2017. 1-23
8. Enrico Kaden, Nathaniel D. Kelm, Robert P. Carson et al. Multi-compartment microscopic diffusion imaging. NeuroImage. 2016. 139(1). 346–359.
9. Jennifer Stine Elama, Matthew F.Glasser et al. The Human Connectome Project: A retrospective. NeuroImage. 2021. 244(1). 1-24
10. L. Cordero-Grande, D. Christiaens et al. Complex diffusion-weighted image estimation via matrix recovery under general noise models. NeuroImage. 2019. 200(1). 391-404
Figures
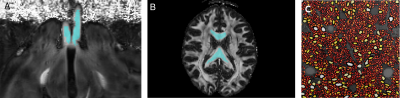
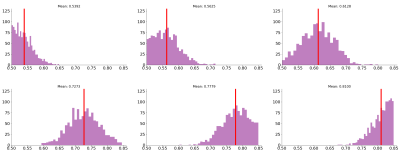
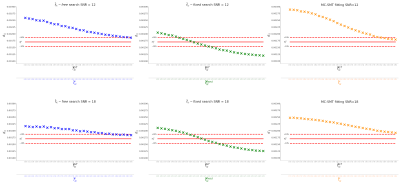
Figure 3. Results for synthetic data that corresponds to the in-vivo HCP acquisition, we compare the performance of a free complete search where $$$f_{ic}$$$ is also estimated (first column), our proposal in the second column (steps 1-2-3-6-7-8 in Methods) vs. the estimation of $$$d_{||}$$$ when performed by the SMT methodology in8( in the last column). Each experiment (panel) shows at the bottom the estimated $$$f^{*}_{ic}$$$ values for each optimization and also the GT values. In some experiments, the degeneration in the fitting incorrectly saturates these values close to 1.
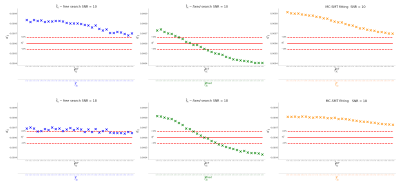
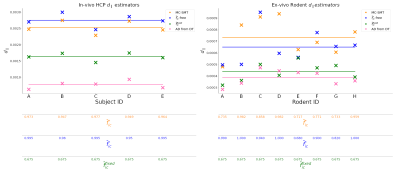
Figure 5. Estimation of $$$d_{||}$$$ on the real in-vivo and ex-vivo datasets using our proposal (steps 1-2-3-6-7-8 and steps 1-2-3-4-5 in Methods), methodology in8 and axial diffusivity (AD) from DT. In the low-SNR scenario (SNR = 12 and 10, respectively) the estimated $$$f^{*}_{ic}$$$ for the free-search and MC-SMT methods show degenerations similarly to our synthetic experiments. Then, the one estimated from the fixed-search method is more reliable. The averaged $$$d_{||}$$$ value with our proposal for the in vivo dataset is 1.63e-9m2/s and for the ex vivo data is 0.436e-9m2/s.