3830
Cross-domain Variational Network for Fast Chemical Exchange Saturation Transfer Imaging1Key Laboratory for Biomedical Engineering of Ministry of Education, Department of Biomedical Engineering, College of Biomedical Engineering & Instrument Science, Zhejiang University, Hangzhou, Zhejiang, China, 2MR Collaboration, Siemens Healthcare Ltd., Shanghai, China
Synopsis
Chemical exchange saturation transfer (CEST) is an emerging molecular imaging technique that can detect various biomolecules in vivo. However, the routine clinical application of CEST MRI is hammered by its long scan time due to the multiple saturation frames acquired. Here, a novel deep neural network modified from the variational network (VN) by utilizing cross-domain regularization structures, dubbed CEST-VN, is proposed for accelerated CEST imaging. In conjunction with multi-coil sensitivity encoding, the CEST-VN method demonstrated superior performance to the conventional parallel imaging and the original VN methods in healthy volunteers and glioma patients.
Introduction
Chemical exchange saturation transfer (CEST) has proven to be a powerful technique that can sensitively detect a wide range of biomolecules and pathologies1-3. However, the widespread clinical adoption of this technique has been hampered by its relatively long scan time. Inspired by the recent variational network (VN) method4, we propose a deep-learning-based approach, termed CEST-VN, which is implemented for rapid CEST imaging. The desired source images can be reconstructed from undersampled multi-coil data by our CEST-VN method, which contains convolutional neural network (CNN)-based structures operating in both the image domain and k-space domain at each stage. Evaluation results show the proposed network outperforms state-of-the-art methods noticeably for both healthy and brain tumor subjects.Theory
Problem Formulation: The general unconstrained image reconstruction problem is given by:$$\begin{equation}\tag{1}{{\bf \hat{u}}=\mathop{argmin}\limits_{\bf u}{\Vert \bf {Eu-f} \Vert}_2^2+\lambda{R( \bf {u})},}\end{equation}$$
where $$$\bf {u}$$$ denotes the desired MR images; $$$\bf {f}$$$ denotes multi-coil undersampled k-space measurements; $$$\bf {E=MFC}$$$ is the encoding operator, in which $$$\bf {C}$$$ denotes coil sensitivity maps, $$$\bf {F}$$$ refers to Fourier transform, and $$$\bf {M}$$$ represents an undersampling matrix; $$$ {\lambda}$$$ is the regularization weight; and $$$R(\cdot)$$$ designates the regularization function. Unlike the original VN method operating in the image domain4, we propose to use a cross-domain regularization function based on deep learning, which is formulated as:
$$\begin{equation}\tag{2}{R(\mathbf{u})=\lambda_{I} D_{i}(\mathbf{u})+\lambda_{K}\left\|\mathbf{u}-\mathcal{F}^{-1} D_{k}(\mathbf{k})\right\|_{2}^{2}.}\end{equation}$$
Specifically, $$$D_{i}(\mathbf{u})=\sum_{i=1}^{N_{k}} \phi_{i}\left(\mathbf{K}_{i} \mathbf{u}\right)$$$can be constructed as an operator representing a relaxed fields-of-experts (FoE) regularization5, which is used to remove artifacts and noise in the image domain. In addition, $$$D_{k}$$$ is an operator used to complete k-space from $$$\mathbf{k}$$$ representing the k-space of $$$\mathbf{u}$$$ at the $$$t$$$-th iteration, and $$$\lambda_{I}$$$ and $$$\lambda_{K}$$$ denote regularization parameters.
The problem of Eqs. (1-2) can be solved using the gradient descent (GD) algorithm:
$$\begin{equation}\tag{3}{\mathbf{u}^{t+1}=\mathbf{u}^{t}-\alpha^{t}\left(2 \mathbf{E}^{*}\left(\mathbf{E} \mathbf{u}^{t}-\mathbf{f}\right)+\lambda_{I} \sum_{i=1}^{N_{k}}\left(\mathbf{K}_{i}\right)^{\top} \phi_{i}^{\prime}\left(\mathbf{K}_{i} \mathbf{u}^{t}\right)+2 \lambda_{K}\left(\mathbf{u}^{t}-\mathcal{F}^{-1} D_{k}\left(\mathbf{k}^{t}\right)\right)\right),}\end{equation}$$
where $$$\mathbf{E}^{*}$$$ represents the adjoint operator performing combined inverse Fourier transform and coil sensitivity encoding, and $$$\alpha^{t}$$$ is the step size at the $$$t$$$-th $$$(t=0, …, T)$$$ iteration.
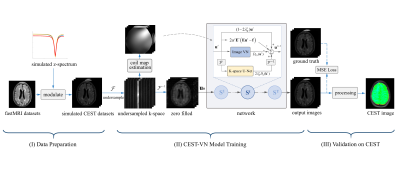
Proposed Network: The iteration scheme of Eq. (3) is unrolled to a network with $$$T$$$ stages, with each representing an update step of the GD algorithm, as depicted in Fig. 1. The image-space operator $$$D_{i}$$$ at each stage is structured by a variational regularization network with trainable activation functions $$$\phi_{i}^{\prime}$$$, and the k-space completion operator $$$D_{k}$$$ is structured based on the U-Net6 architecture.
Methods
As illustrated in Fig. 1, our work can be divided into three stages: data preparation, CEST-VN model training, and validation on real CEST data. As for data preparation, z-spectra simulated by the Bloch-McConnell equation were used to modulate the fastMRI7 open dataset that includes multi-coil FLAIR, T1-weighted, and T2-weighted brain MR data. Before training, the original k-space data were retrospectively undersampled using a variable density Cartesian mask with a reduction factor of R=3, and coil sensitivity maps were calculated from the ACS data using ESPIRiT8. Importantly, no actual CEST data were exposed to CEST-VN until the validation phase. We conducted the training using the RMSProp algorithm9 to minimize a mean squared error (MES) loss, during which fully-sampled images were regarded as ground-truth.Human experiments were conducted on a 3T Siemens Prisma MRI system with a 64-channel-receive head coil. A single-slice TSE-CEST sequence10 was run with 63 saturation offsets acquired. Plus, a dual-echo GRE sequence was used for B0 field mapping. The trained CEST-VN network was applied to retrospectively undersampled CEST data from a healthy volunteer and a glioma patient for validation. And then, the amide proton transfer weighted (APTw) image was calculated by the magnetization transfer ratio asymmetry analysis using source images from the output of our network.
Results
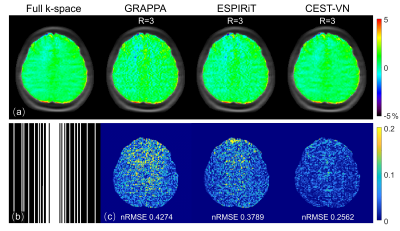
Fig. 2 depicts the fully-sampled reference APTw map in comparison with those 3-fold accelerated ones reconstructed with GRAPPA11, ESPIRiT8, and CEST-VN on the healthy volunteer. CEST-VN yielded a better agreement with the reference image and a smaller error than the other parallel imaging methods when using the same retrospectively undersampled data. Similarly, Fig. 3 depicts the comparison of various reconstruction methods on a newly-diagnosed glioma patient. Compared to conventional parallel imaging reconstruction, CEST-VN shows superior performance in both artifact removal and detail retention, especially for lesion tissues. Fig. 4 presents three popular metrics for evaluating accelerated reconstruction quality against the reference full k-space images at different saturation offsets. CEST-VN generated lower nRMSE, higher SSIM and PSNR than parallel imaging and the original VN4 methods, demonstrating its improved and robust performance for various saturation offsets.Conclusion
In this work, we presented a novel deep neural network modified from the variational network with a cross-domain regularization structure for fast multi-coil CEST imaging. Our CEST-VN method yielded superior performance in terms of both image quality and reconstruction errors, compared to the state-of-the-art methods. Notably, the CEST-VN method does not use any actual CEST data during the network training, proving its good generalizability. To the best of our knowledge, this is the first work integrating deep-learning and parallel imaging approaches to accelerate CEST imaging for clinical multi-coil data.Acknowledgements
NSFC grant numbers: 61801421 and 81971605. Leading Innovation and Entrepreneurship Team of Zhejiang Province: 2020R01003. This work was supported by the MOE Frontier Science Center for Brain Science & Brain-Machine Integration, Zhejiang University.
References
1. van Zijl PC, Lam WW, Xu J, Knutsson L, Stanisz GJ. Magnetization Transfer Contrast and Chemical Exchange Saturation Transfer MRI. Features and analysis of the field-dependent saturation spectrum. Neuroimage. 2018;168:222-241.
2. Jones KM, Pollard AC, Pagel MD. Clinical applications of chemical exchange saturation transfer (CEST) MRI. Journal of Magnetic Resonance Imaging. 2018;47(1):11-27.
3. Zhou J, Heo HY, Knutsson L, van Zijl PCM, Jiang S. APT-weighted MRI: Techniques, current neuro applications, and challenging issues. Journal of magnetic resonance imaging: JMRI. 2019;50(2):347-364.
4. Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, Knoll F. Learning a variational network for reconstruction of accelerated MRI data. Magnetic Resonance in Medicine. 2018;79(6):3055-3071.
5. Roth S, Black MJ. Fields of Experts. International Journal of Computer Vision. 2009;82(2):205.
6. Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. 2015:234-241.
7. Zbontar J, Knoll F, Sriram A, Murrell T, Huang Z, Muckley MJ, Defazio A, Stern R, Johnson P, Bruno M. fastMRI: An open dataset and benchmarks for accelerated MRI. arXiv preprint arXiv:181108839, 2018.
8. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT-An Eigenvalue Approach to Autocalibrating Parallel MRI: Where SENSE Meets GRAPPA. Magnetic Resonance in Medicine. 2014;71(3):990-1001.
9. Tieleman T, Hinton G. Divide the gradient by a running average of its recent magnitude. COURSERA Neural Netw. Mach Learn. 2012;6:26-31.
10. Liu R, Zhang H, Niu W, Lai C, Ding Q, Chen W, Liang S, Zhou J, Wu D, Zhang Y. Improved chemical exchange saturation transfer imaging with real-time frequency drift correction. Magnetic resonance in medicine. 2019;81(5):2915-2923.
11. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang JM, Kiefer B, Haase A. Generalized Autocalibrating Partially Parallel Acquisitions (GRAPPA). Magnetic Resonance in Medicine. 2002;47(6):1202-1210.
Figures