3818
Fast parameters Mapping in the brain 4-pool model from tsDESPOT acquired data within 10 seconds using deep learning.1Advanced Technology Research Dept., CANON MEDICAL SYSTEMS CORPORATION, Kawasaki-shi, Japan, 2Advanced Technology Research Dept., CANON MEDICAL SYSTEMS CORPORATION, Ootawara-shi, Japan
Synopsis
In quantitative imaging of the brain, it is common that tissues having different T1 and T2 values are mixed in a voxel and exchange proton each other. So multiparametric imaging method of brain microstructure is attracting much attention. In this study, we demonstrated that quantitative maps of 12 parameters in the brain 4-pool model (2 free water pools with exchange and 2 semi-solid water pools) were estimated within 10 seconds using deep learning from the data acquired by the tsDESPOT sequence.
Introduction
For multiparametric imaging method of brain microstructure, mcDESPOT based on a 2-pool model is known. However it takes a long time for analysis1 and some issues have been reported2,3. There are some other methods, most methods do not consider exchange of protons between free water pools and existence of semi-solid water (MT) pools, so in some cases, there may be a difference from the physical reality.In this study, we have demonstrated that quantitative maps of 12 parameters in the brain 4-pool model4 were estimated within 10 seconds using deep learning from the data acquired by the transient state DESPOT (tsDESPOT) sequence5 which take some images using spoiled gradient echo (SP-GRE) and FISP with different flip angles (FA).
Methods
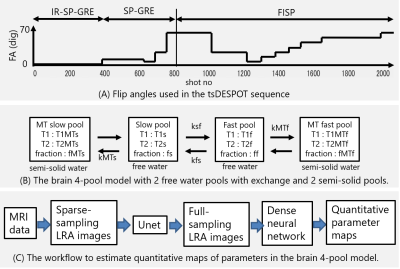
Imaging was performed with prototype radial2D tsDESPOT sequence. First, Inversion recovery (IR)-SP-GRE and SP-GRE was used to acquire images with different 4 FAs, and then magnetizations were saturated by SP-GRE with FA 70 degrees, and FISP was used to acquire images with different 9 FAs. Fig.1 (A) shows used FAs. TR / TE = 7.1ms / 3.3ms, Matrix size was 256 x 256, and the scan duration was about 15s. To improve SNR, the scan was performed four times with the initial spoke angle changed by 45 °. A Vantage Galan 3T (Canon Medical Systems, Tochigi, Japan) scanner and a QD head coil were used for imaging.Fig.1(B) shows used brain 4-pool model. We assumed T1 of MT pools (T1MTs, T1MTf) were equal to T1 of exchanged free water pools (T1s, T1f) respectively, T2 of MT pools (T2MTs, T2MTf) were 10µs, and total fraction (fs+ff+fMTs+fMTf) was100%.
Fig.1(C) shows workflow to estimate quantitative maps in the brain 4-pool model. Sparse-sampling low rank approximated (SS-LRA) images5,6 were calculated from acquired data, and full-sampling low rank approximated (FS-LRA) images were estimated using Unet, and then quantitative parameter maps were estimated using dense neural network (DNN). Details are described below.
To generate SS-LRA images, about 200,000 magnetization evolution curves at various parameters values were calculated using extended phase graph with exchange7, and coefficients for generating SS-LRA images were obtained by principal component analysis. From the data of (IR-)SP-GRE part and FISP part, 13 SS-LRA images were generated individually. Because SS-LRA images have sparse artifacts, FS-LRA images were estimated using Unet. For training the Unet, about 9000 set of SS-LRA images and FS-LRA images were created by imaging simulation of randomly generated numerical brain phantoms based on BrainWeb8. The training was done for about a week. Parameter maps ware estimated voxel by voxel using DNN from estimated FS-LRA images. For training the DNN, about 8 million data sets of LRA values and parameters value were used. The training was done for about a day.
Results
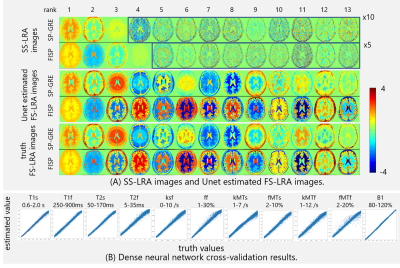
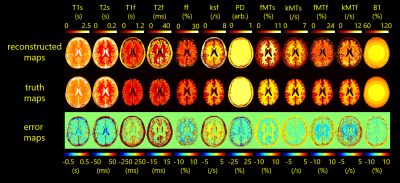
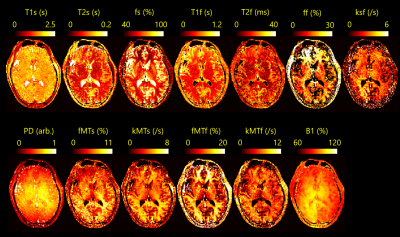
FS-LRA images could be estimated by the Unet from SS-LRA images that were generated by imaging simulation of numerical brain phantom (Fig.2(A)). SS-LRA images, especially in the case of high rank had many sparse artifacts. However, the Unet was able to estimate FS-LRA image. From The cross-validation results of the DNN (Fig.2(B)), It was found that parameters in the brain 4-pool model can be estimated from LRA values.Using the proposed workflow, parameter maps were successfully estimated from the data that was generated by imaging simulation of numerical brain phantom (Fig.3). However, three types of errors were seen on them and discussed later. Also, parameter maps of volunteer were estimated from the data acquired by tsDESPOT (Fig.4) within 10 seconds.
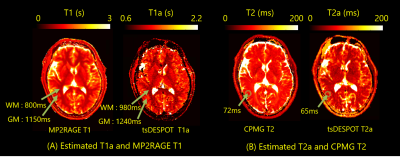
Additionally, apparent T1 and T2 (T1a and T2a) maps were calculated from estimated brain 4-pool model parameters (Fig.5). “apparent” means that it is a value obtained by single compartment method. T1a and T2a were almost consistent with T1 measured by MP2RAGE and T2 measured by CPMG respectively.
Discussion
In this study, we demonstrated the method of estimating parameter maps in the brain 4-pool model using deep learning. However, there were some issues.FS-LRA images estimated using the Unet had some errors, and errors in SP-GRE tended to be larger than in FISP. The reason for this may be that there were too few SP-GRE images in the sequence. Estimated parameter maps of numerical brain phantom shown mainly three types of error. (1) Error of gray matter T2f. It may happen due to small ff (fraction of fast pool) in gray matter. (2) Errors like B1 distribution. This seems to be related to too few SP-GRE images that are important to estimate B1. (3) Errors at white matter / gray matter boundary. It may happen due to too few variations in the training dataset for Unet. These errors may be eliminated by optimizing sequence and increasing variation of training dataset. Also, as previously reported, accuracy may be improved by guarantee data consistency using LRA Unet ADMM (alternating direction method of multipliers) method5.
Estimated parameter maps of volunteer seems to have some issues too. The validity of these results needs to be examined with the improvement of accuracy.
Conclusion
In this study, we have demonstrated that quantitative maps of 12 parameters of the brain 4-pool model were estimated within 10 seconds using deep learning from the data acquired by the tsDESPOT sequence.Acknowledgements
No acknowledgement found.References
1. Sean C. L. Deoni, Lucy Matthews, Shannon H. Kolind, One Component? Two Components? Three? The Effect of Including a Nonexchanging ‘‘Free’’ Water Component in Multicomponent Driven Equilibrium Single Pulse Observation of T1 and T2, Magn. Reson. Med. 70, 147-154(2013)
2. Daniel J. West, Rui P.A.G. Teixeira, Tobias C. Wood, Joseph V. Hajnal, Jacques-Donald Tournier, Shaihan J. Malik, Inherent and unpredictable bias in multi-component DESPOT myelin water fraction estimation, NeuroImage 195, 78-88(2019)
3. Adam V. Dvorak, Emil Ljungberg, Irene M. Vavasour, Lisa Eunyoung Lee,Shawna Abel, David K. B. Li, Anthony Traboulsee, Alex L. MacKay, Shannon H. Kolind, Comparison of multi echo T2 relaxation and steady state approaches for myelin imaging in the central nervous system, Scientific Reports 11, 1369(2021).
4. T.A. Bjarnason, I.M. Vavasour, C.L.L. Chia, A.L. MacKay, Characterization of the NMR Behavior of White Matter in Bovine Brain, Magn. Reson. Med. 54, 1072-1031 (2005).
5. Yuuzo Kamiguch, Sadanori Tomiha, Masao Yui, Accurate quantitative parameter maps reconstruction method for tsDESPOT using Low Rank approximated Unet ADMM, Proc. Intl. Soc. Mag. Reson. Med. 28, 2174 (2021)
6. Assländer J, Cloos MA, Knoll F, Sodickson DK, Hennig J, Lattanzi R. Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magn. Reson. Med. 79 83–96 (2018)
7. Shaihan J. Malik, Rui Pedro A.G. Teixeira, Joseph V. Hajnal, Extended phase graph formalism for systems with magnetization transfer and exchange, Magn. Reson. Med. 80, 767-779 (2018)
8. C.A. Cocosco, V. Kollokian, R.K.-S. Kwan, A.C. Evans , BrainWeb: Online Interface to a 3D MRI Simulated Brain Database, NeuroImage, vol.5, no.4, part 2/4, S425, 1997 -- Proceedings of 3-rd International Conference on Functional Mapping of the Human Brain, Copenhagen, May 1997.
Figures