3806
Learning White Matter Streamline Representations Using Transformer-based Siamese Networks with Triplet Margin Loss
Shenjun Zhong1, Zhaolin Chen1, and Gary Egan1
1Monash Biomedical Imaging, Monash University, Australia, Melbourne, Australia
1Monash Biomedical Imaging, Monash University, Australia, Melbourne, Australia
Synopsis
Robust latent representation of white matter streamlines are critical for parcellating streamlines. This work introduced a novel transformer-based siamese network with triplet margin loss, that learns to embed any lengths of streamlines into fixed-length latent representations. Results showed that a minimum of two layers of transformer encoders were sufficient to model streamlines with a very limited number of training data.
Introduction
Embedding tractography streamlines into fixed-length latent representations improves the effectiveness of streamline parcellation. Unlike manually designed features, e.g. distance-based methods [1-4], deep learning-based algorithms were designed to learn latent representations, such as 1D convolutional neural network (CNN) [5], 2D CNN [6] and recurrent neural networks (RNN) [7]. However, CNNs fail to model the sequential information of streamlines, and traditional RNNs, e.g. Long Short Term Memory (LSTM), are weak in modeling long dependencies.In this work, we proposed and validated a siamese network with transformer encoders that models streamlines via bidirectional self-attention mechanism, and are capable of capturing long dependencies in a sequence [8]. We applied triplet margin loss [9] to explore the representation power of transformer-based architectures. The results showed that the transformer-based encoders can achieve high performance with minimal labelled data.
Methods
DatasetThe dataset used in the study is from the “ISMRM 2015 Tractography Challenge” [10], which contained 200,432 streamlines and were annotated into 25 pre-defined major bundle types including corpus callosum (CC), left and right corticospinal tract (CST), and etc. Streamlines were splitted into training samples (80%) and testing samples (20%). To optimize the neural network with triplet margin loss, the streamlines were further randomly sampled to form triplets, in the format of (anchor, positive, negative) pairs.
Model and Loss Function
In figure 1, it shows the model architecture and the training workflow. The triplets were generated on the fly, zero-padded to length of 512 and fed into the same siamese network to encode the streamline sequences into latent vectors for the anchor, positive and negative streamlines respectively. The encoder was a composite of a linear layer and several transformer layers that learned the representation of the input sequence. Each transformer layer used a hidden dimension of 64, 4 heads and 128 feedforward dimensions.
Triplet margin loss was used to train the neural network, and the basic idea was to pull streamlines belonging to the same bundle closer in the latent space while pushing streamlines from different bundle types apart. The loss, L is defined as
$$L(a,p,n) = max \left \{ \right. d(a_i,p_i)-d(a_i,n_i)+margin, 0 \left \} \right.$$
where margin is 1.0 and d is the L2 norm distance measurement, i.e.
$$d(x_i,y_i) = \left \| x_i-y_i \right \|_{2}$$
Experimental Setup
In order to explore the representation power of transformer-based encoders, the experiments were conducted using one, two and three layer(s) of transformers respectively and the models were trained using various proportions of training samples, from 0.4% to 100% of the training data, as shown in figure 2(a).
The models were trained for 50000 iterations when 100% of the training data were used, and for a reduced number of iterations, when only proportion of the training data were used. All the models were trained with a batch size of 32.
To validate the models, 9600 triplets were randomly generated from the samples in the testing data. The models were validated by measuring the accuracy where the prediction was regarded as correct when the Euclidean distance between the anchor and positive samples was shorter than the distance between the anchor and the negative samples, and vice versa.
Results and Discussion
In figure 3, it showed the validation performance of the three transformer encoders (i.e. one layer, two layers and three layers) when various numbers of training data were used. A >98% triplet accuracy was achieved with only 0.4% of the training data for all the encoders. The two- and three-layer transformer networks performed similarly with various training samples, and they performed better while increasing the training data. On the other hand, the one-layer transformer network failed to improve the performance until 3-4% of training data were used, and its performance dropped significantly when models were trained with 5%-9% of training data. With more than 10% of the training data used, there was no significant improvement observed for all the neural network configurations.Figure 4 shows the distributions of margins between the distance of (anchor, positive) pair and (anchor, negative) pair. Similar to the triplet accuracy in figure 3, the two- and three-layer transformer encoders were able to push the margin value above 5, while the margin of the one-layer counterpart were below 5 in most of the cases. Larger margin value means a clearer separation plane in high dimension space.
During validation, we obtained the latent vectors of some major bundles, performed unsupervised clustering using the Kmean algorithm and visualized their 2D projections. With only 1 streamline used for model training per bundle, anterior commissures (CA) and posterior commissures (CP) were perfectly separated (figure 2(b)), and similarly for symmetric structures, like left and right frontopontine tracts (FPT) as shown in figure 5(a) and figure 5(b). In their 2D projections, separation planes could be clearly observed. In figure 5(c), tests were performed for bundles with similar endpoints, including CST, FPT and parieto-occipital pontine tract (POPT), which were also clearly clustered.
Conclusion
In this work, we introduced a novel transformer-based siamese network to learn fixed-length streamline latent representations via triplet margin loss. Results showed that a minimum of two layers of transformer encoders were sufficient to model streamlines with a very limited number of training data.Acknowledgements
No acknowledgement found.References
- Maddah, M., Mewes, A. U., Haker, S., Grimson, W. E. L., & Warfield, S. K. (2005, October). Automated atlas-based clustering of white matter fiber tracts from DTMRI. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 188-195). Springer, Berlin, Heidelberg.
- Clayden, J. D., Storkey, A. J., & Bastin, M. E. (2007). A probabilistic model-based approach to consistent white matter tract segmentation. IEEE transactions on medical imaging, 26(11), 1555-1561.
- Corouge, I., Gouttard, S., & Gerig, G. (2004, April). Towards a shape model of white matter fiber bundles using diffusion tensor MRI. In 2004 2nd IEEE International Symposium on Biomedical Imaging: Nano to Macro (IEEE Cat No. 04EX821) (pp. 344-347). IEEE.
- Labra, N., Guevara, P., Duclap, D., Houenou, J., Poupon, C., Mangin, J. F., & Figueroa, M. (2017). Fast automatic segmentation of white matter streamlines based on a multi-subject bundle atlas. Neuroinformatics, 15(1), 71-86.
- Legarreta, J. H., Petit, L., Rheault, F., Theaud, G., Lemaire, C., Descoteaux, M., & Jodoin, P. M. (2021). Filtering in Tractography using Autoencoders (FINTA). Medical Image Analysis, 102126.
- Chen, Y., Zhang, C., Song, Y., Makris, N., Rathi, Y., Cai, W., ... & O’Donnell, L. J. (2021, September). Deep Fiber Clustering: Anatomically Informed Unsupervised Deep Learning for Fast and Effective White Matter Parcellation. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 497-507). Springer, Cham.
- Zhong, S., Chen, Z., & Egan, G. (2021). Auto-encoded Latent Representations of White Matter Streamlines for Quantitative Distance Analysis. bioRxiv.
- Wolf, T., Chaumond, J., Debut, L., Sanh, V., Delangue, C., Moi, A., ... & Rush, A. M. (2020, October). Transformers: State-of-the-art natural language processing. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations (pp. 38-45).
- Hermans, A., Beyer, L., & Leibe, B. (2017). In defense of the triplet loss for person re-identification. arXiv preprint arXiv:1703.07737.
- Maier-Hein, K. H. et al. (2015) Tractography Challenge ISMRM 2015 Data. https://doi.org/10.5281/zenodo.572345
Figures
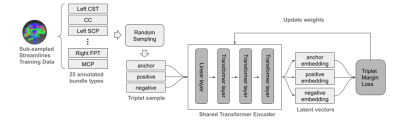
Figure 1. Model architecture and training process.
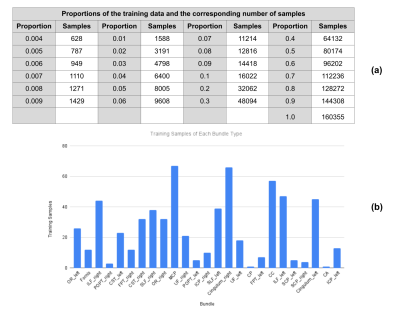
Figure 2. Training data proportions and sample distribution of the minimal training dataset.
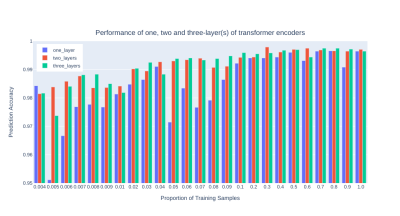
Figure 3. Performance of one, two and three-layer(s) of transformer encoders under different proportions of training samples.
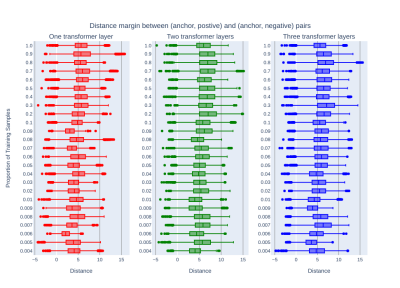
Figure 4. The distribution of margins between the (anchor, positive) and (anchor, negative) pairs.
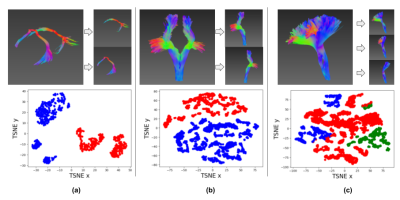
Figure 5. Streamline clustering and 2D projection visualization.
DOI: https://doi.org/10.58530/2022/3806