Introduction

Conventional parallel imaging methods utilize the spatial encoding by array of receiver coils to unfold the periodic aliasing artifact resulted from uniformly undersampled k-space data in image, frequency or hybrid domains (e.g., SENSE¹ and GRAPPA²). Low- and ultra-low-field MRIs are presently undergoing a renaissance for low-cost, portable, or/and point-of-care (but value-adding) applications^3-7. However, effective receiver coil arrays often do not exist in these systems with simple hardware, and their intrinsic signal SNRs are low. Thus, the conventional parallel imaging methods are not generally applicable.
Intuitively, the violation of Nyquist-Shannon sampling theorem due to k-space uniform undersampling leads to periodic aliasing in the image domain. Such periodicity is well-defined by the known imaging FOV and acceleration factor⁸, rendering the aliasing artifact a fully predictable pattern. Given the robust pattern recognition ability of deep neural networks, the image artifact periodicity can be potentially learned from prior pair of undersampled and fully sampled data. One recent paper proposed using a conventional U-Net to achieve dealiasing on single-channel magnitude data⁹, but its simple simulation did not factor in the complex nature of MR data and only demonstrated limited acceleration. In this study, we propose a U-Net based single-channel reconstruction framework that specifically exploits the periodicity of aliasing artifact.

Methods

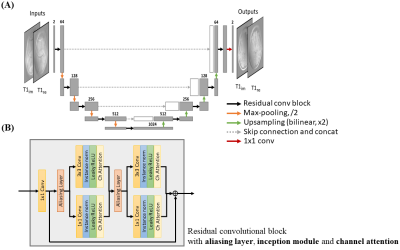
Model Architecture: A U-Net, containing down- and up-sampling layers, is adopted as the model backbone to extract both fine and coarse features of the aliased image input (Figure 1). Convolution blocks with residual connection are used to learn the periodic residual aliasing artifact. To further facilitate the learning of the periodic aliasing, three modules are introduced as following:
(1) Aliasing layer⁸, a preprocessing layer inserted before convolution layer utilizing the aliasing periodicity, shifts the aliased input according to the acceleration rate to align and to enable the non-local yet spatially correlated regions to perform a standard convolution operation. The shifted images are concatenated along the channel dimension.
(2) Inception module¹⁰, consisting of convolution layers with different kernel sizes of 3x3 and 1x1 executed in parallel, is used rather than typical convolution of single kernel size. 3x3 convolution extracts local features of the input while 1x1 convolution discards local information of the input and aims specifically at learning the relation of the periodic aliased pixels provided by aliasing layer. The principle of 1x1 convolution following the aliasing layer is analogous to the linear equation formulated in SENSE but in single-channel manner.
(3) Channel attention¹¹, inserted after inception module, serves as a self-regulator that implicitly regularizes the feature extraction of preceding convolutions.
Implementation Details: The U-Net consisted of four pooling and up-sampling layers. The number of channels of the first convolution block was 64, which was doubled and halved after every pooling and up-sampling layers respectively. Real and imaginary components of complex image were treated as separate input channels. The network was trained with Adam optimizer with initial learning rate 10^-4, decay factor of 0.1 per 10 epochs, and l₂ loss function for 60 epochs on a RTX3090 for approximately 22 hours. Separate models were trained on individual contrasts for optimized performance. K-space correction was performed after the model for consistency of acquired data.
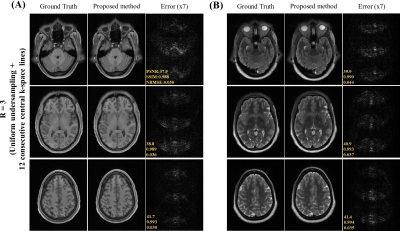
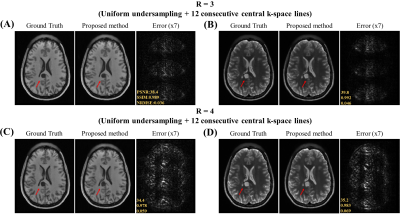
Data Preparation: The HCP S1200 dataset¹² including T1 and T2 weighted images from normal subjects were used. 400 MR data were split into ratio of 8:1:1 for training, validation and testing respectively for each contrast. Image downsampling of factor 2 was done to alleviate the GPU memory burden and to expedite the training in this study, resulting in axial in-plane geometry: FOV = 224x180mm² and spatial resolution = 1.4x1.4mm². Random 2D phase maps were introduced to simulate the complex nature of MR data. The k-space data was retrospectively undersampled with acceleration R = 3 and 4 using 1D cartesian uniform sampling masks plus 12 consecutive central k-space lines.
SSIM, PSNR and NRMSE were used to quantitatively evaluate the reconstructed images. The proposed method was also evaluated with images containing pathological anomalies unseen in the training dataset.

Results

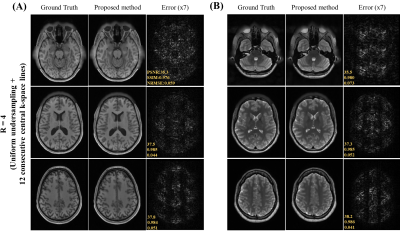
Figure 2 show the unfolding capability of the method to remove the periodic aliasing artifact on single-channel data at R=3 (effective R_eff=2.61) in T1- and T2-weighted images. High acceleration R=4 (effective R_eff=3.27) were also successfully achieved (Figure 3). Figure 4 illustrates the robustness of the proposed method on unfolding an unseen anomaly, which was not included in the training dataset. Moreover, no apparent noise amplification and blurring were observed.

Discussion and Conclusion

We present a neural network with tailored components for cartesian uniform undersampling by explicitly utilizing the sampling pattern specific periodicity. The results demonstrated its robust performance for unfolding the image aliasing artifact at high acceleration, with no noise amplifications, and in presence of unseen pathologies. This new method offers a promising approach to highly accelerated single-channel MRI for low-cost single-channel mid-, low- and ultra-low-field platforms.

Acknowledgements

This work was supported in part by Hong Kong Research Grant Council (R7003-19F, HKU17112120 and HKU17127121 to E.X.W., and HKU17103819, HKU17104020 and HKU17127021 to A.T.L.L.), and Lam Woo Foundation to E.X.W..

References

1. K. P. Pruessmann, M. Weiger, M. B. Scheidegger, and P. Boesiger, “SENSE: Sensitivity encoding for fast MRI,” Magn. Reson. Med., vol. 42, no. 5, pp. 952–962, 1999.

2. M. A. Griswold et al., “Generalized Autocalibrating Partially Parallel Acquisitions (GRAPPA),” Magn. Reson. Med., vol. 47, no. 6, pp. 1202–1210, 2002.

3 J. P. Marques, F. F. J. Simonis, and A. G. Webb, “Low-field MRI: An MR physics perspective,” J. Magn. Reson. Imaging, vol. 49, no. 6, pp. 1528–1542, Jun. 2019.

4. L. L. Wald, P. C. McDaniel, T. Witzel, J. P. Stockmann, and C. Z. Cooley, “Low-cost and portable MRI,” J. Magn. Reson. Imaging, vol. 52, no. 3, pp. 686–696, Sep. 2020.

5. T. O’Reilly, W. M. Teeuwisse, D. de Gans, K. Koolstra, and A. G. Webb, “In vivo 3D brain and extremity MRI at 50 mT using a permanent magnet Halbach array,” Magn. Reson. Med., vol. 85, no. 1, pp. 495–505, Jan. 2021.

6. C. Z. Cooley et al., “A portable scanner for magnetic resonance imaging of the brain,” Nat. Biomed. Eng., vol. 5, no. 3, pp. 229–239, 2021.

7. Liu Y, Leong ATL, Zhao Y, Xiao L, Mak HKF, Tsang A, Lau GKK, Leung GKK, Wu EW., “A Low-cost and Shielding-free Brain MRI Scanner for Accessible Healthcare,” Nature Communications, 2022 (In Press).

8. H. Takeshima, “Aliasing layers for processing parallel imaging and EPI ghost artifacts efficiently in convolutional neural networks,” Magn. Reson. Med., 2021.

9. C. M. Hyun, H. P. Kim, S. M. Lee, S. Lee, and J. K. Seo, “Deep learning for undersampled MRI reconstruction,” Phys. Med. Biol., vol. 63, no. 13, p. aac71a, 2018.

10. C. Szegedy et al., “Going deeper with convolutions,” in Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2015, vol. 07-12-June, pp. 1–9.

11. S. Woo, J. Park, J. Y. Lee, and I. S. Kweon, “CBAM: Convolutional block attention module,” in Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 2018, vol. 11211 LNCS, pp. 3–19.

12. Van Essen, D.C., et al: The wu-minn human connectome project: an overview. Neuroimage 80, 62-79, 2013.