3567
3D Golden Angle Stack-of-Spiral bSSFP Sequence for Undersampled Lactate Imaging in Hyperpolarized MRI1University of California San Francisco, San Francisco, CA, United States, 2HeartVista, Los Altos, CA, United States
Synopsis
In the previous work, 3D balanced steady state free precession (bSSFP) sequence have been used to improve SNR for hyperpolarized 13C lactate imaging. In this study, we proposed a 3D bSSFP stack-of-spiral with golden angle rotation sequence for lactate imaging to furtherly accelerate lactate imaging. At the same time, we designed a regularized reconstruction method for the undersampled data that did not degrade image quality.
Introduction
MRI of hyperpolarized 13C-labeled compounds is a useful tool to non-invasively detect metabolic processes. As one application, hyperpolarized [1-13C]pyruvate has been translated into clinical studies for assessing cancer and cardiac metabolism. [1,2] However, hyperpolarized 13C data acquisition is challenged to achieve high SNR and high resolution, because of the depleted signal. In previous work, a 3D balanced steady state free precession (bSSFP) [3-7] sequence has been used to improve 13C-lactate imaging. In this study, we proposed a 3D bSSFP stack-of-spiral with golden angle rotations for lactate imaging to furtherly accelerate lactate imaging. At the same time, we designed a regularized reconstruction method for the undersampled data without degrading image quality.Methods
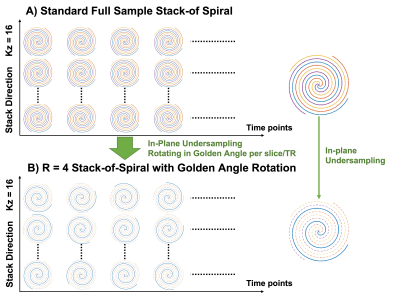
Sequence Design: The standard 3D bSSFP stack-of-spiral lactate specific imaging trajectory (Figure 1A) was using the same spiral trajectory with four interleaves to acquire all slices and stacks lactate data. To accelerate lactate imaging acquisition, the proposed trajectory (Figure 1B) with R=4 in-plane undersampling ratio was based on the same 3D bSSFP stack-of-spiral framework. At the same time, to achieve a pseudo-randomized sampling pattern, the spiral trajectory was rotated by the golden angle ratio in each TR of all acquisition time.Reconstruction Process: All dynamic 3D lactate data were jointly reconstructed. The signal model can be presented as: $$S_{k,m,t}={FFT}_z\left(NUFFT(C_m\rho_t)\right)+\eta\qquad(1)$$ where $$$t$$$ is the t-th time points, $$$C_m$$$ is the m-th channel coil sensitivity map, $$$\eta$$$ is gaussian noise. Rewriting the Fourier Transform term into encoding matrix form as $$$E$$$, the dynamic images can be derived by solving an optimization problem: $$\arg\min_{ρ_t}\parallel{E(C_mρ_t)-S_{k,m,t}}\parallel_2^2+\parallel{R_r(ρ_t)}\parallel_*\qquad(2)$$ where the nuclear norm of $$$R_r(z_t)$$$ provides locally low rank regularization [8]. Equation (2) was solved by ADMM [9].
In Vivo Data: Two datasets of patients with renal tumors prior to surgical resection were acquired by standard 3D bSSFP stack-of-spiral lactate specific sequence and full sampled 3D bSSFP stack-of-spiral with golden angle rotations lactate specific sequence respectively. In vivo data were acquired on a 3T GE scanner (MR750, Waukesha, WI) with an 8-channel QTAR coil (Clinical MR Solutions, Brookfield, WI), following one injection of [1-13C]pyruvate pre-polarized in a 5T GE SPINlab polarizer. 13C kidney images of [1-13C] pyruvate data were acquired by a multi-slice 2D spiral gradient-echo readout. Sequence was implemented on a commercial software (RTHawk, HeartVista, CA). Scan parameters of two patients are the same. To simulate undersampling, only the data from first interleaf of both 3D lactate datasets were selected for the reconstruction.
Results
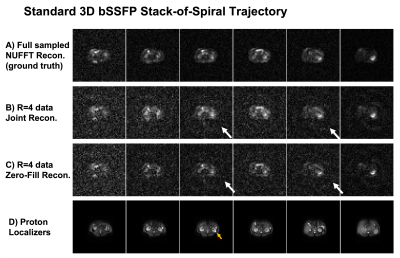
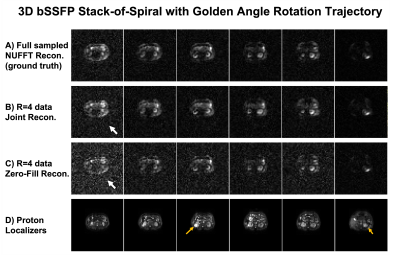
Figure 2&3 show the reconstructions of standard 3D bSSFP stack-of-spiral (Figure 2) and the proposed 3D bSSFP stack-of-spiral with golden angle rotations (Figure 3) lactate images. Full sampled lactate data was reconstructed by the NUFFT method (Figure 2A&3A), working as the ground truth. The undersampled data (R=4) was reconstructed by the proposed joint reconstruction method with a locally low rank constraint (Figure 2B&3B) as well as a zero-filled reconstruction (Figure 2C&3C). As shown by the white arrows in Figure 2B&2C, the undersampled standard stack-of-spiral trajectory has an aliasing artifact, which cannot be removed by both reconstruction processes. [10] However, the artifact of undersampled golden angle rotating stack-of-spiral is a noise-like artifact (white arrow, Figure 3C), which can be suppressed by the locally low rank penalty during the iterative process due to data sparsity (white arrow, Figure 3B). [10]Figure 4 shows two slices with kidney dynamic lactate images, which use the same data and reconstruction methods as Figure 3. The images reconstructed by the zero-filled method has higher noise signal. With locally low rank constraint reconstruction, the noise can be suppressed, and the images have a similar pattern as reconstructions from fully sampled data.
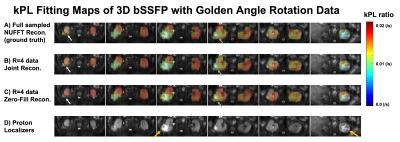
Figure 5 shows kPL kinetic model fitting maps [11] based on the lactate reconstructions by the three reconstruction methods, which use the same data as Figure 3. The white arrows show the bottom of the tumor, and the grey arrows show the top of the tumor. The lactate data reconstructed by the joint reconstruction method with locally low rank constraint can measure a similar kPL value as the ground truth in these two slices. However, the lactate data from zero-filled reconstruction method measures an erroneous higher kPL value at the tumor region.
Discussion & Conclusion
This work describes a joint reconstruction with locally low rank regularization for undersampled 3D bSSFP stack-of-spiral with golden angle rotations lactate imaging data. Comparing with standard 3D bSSFP stack-of-spiral trajectory with the same undersampling ratio, the undersampled spiral trajectory with golden angle rotations has noise-like artifacts that can be suppressed by solving an optimization problem. Based on the Figure 5, undersampled lactate data with proposed reconstruction does not change the quantity of results as full sampled lactate data. Further work is extending the application for lactate imaging acceleration and higher resolution lactate imaging for in vivo hyperpolarized [1-13C] pyruvate studies.Acknowledgements
This work was supported by NIH Grants P41EB013598, R21DK130002, R01CA249909, U01EB026412, and American Cancer Society Grant RSG‐18‐005‐01‐CCE.References
[1] Ardenkjær-Larsen, Jan H., et al. "Increase of signal-to-noise of more than 10,000 times in liquid state NMR." Discovery medicine 3.19 (2003): 37-39.
[2] Golman, Klaes, and Mikkel Thaning. "Real-time metabolic imaging." Proceedings of the National Academy of Sciences 103.30 (2006): 11270-11275.
[3] Svensson J. Hyperpolarized 13C MR angiography using trueFISP. Magn Reson Med 2003;50.
[4] Leupold J, Månsson S, Petersson JS, et al. Fast multiecho balanced SSFP metabolite mapping of 1H and hyperpolarized 13C compounds. MAGMA 2009;22:251–6.
[5] von Morze C, Sukumar S, Reed GD, et al. Frequency-specific SSFP for hyperpolarized 13C metabolic imaging at 14.1 T. Magn Reson Imaging 2013;31:163–70.
[6] Reed GD, von Morze C, Bok R, et al. High resolution (13)C MRI with hyperpolarized urea: in vivo T(2) mapping and (15)N labeling effects. IEEE Trans Med Imaging 2014;33:362–71.
[7] Tang, Shuyu, et al. "A metabolite‐specific 3D stack‐of‐spiral bSSFP sequence for improved lactate imaging in hyperpolarized [1‐13C] pyruvate studies on a 3T clinical scanner." Magnetic resonance in medicine 84.3 (2020): 1113-1125.
[8] Tamir, Jonathan I., et al. "Targeted rapid knee MRI exam using T2 shuffling." Journal of Magnetic Resonance Imaging 49.7 (2019): e195-e204.
[9] Boyd, Stephen, Neal Parikh, and Eric Chu. Distributed optimization and statistical learning via the alternating direction method of multipliers. Now Publishers Inc, 2011.
[10] Lustig, Michael, et al. "Compressed sensing MRI." IEEE signal processing magazine 25.2 (2008): 72-82.
[11] Sahin Sule, Tang Shuyu, Vaidya Manushika, Larson Peder. Fitting kinetic rate constants in metabolite-specific bSSFP hyperpolarized [1-13C]pyruvate MRI. ISMRM 2021 abstract.
Figures