3560
High-SNR J-Resolved MRSI by Jointly Learning Nonlinear Representation and Projection1Department of Bioengineering, University of Illinois Urbana-Champaign, Urbana, IL, United States, 2Beckman Institute for Advanced Science and Technology, Urbana, IL, United States, 3Cancer Center at Illinois, Urbana, IL, United States
Synopsis
J-resolved 1H-MRSI offers several unique advantages but suffers from long acquisition time and lmited SNR, especially for longer TEs. Leveraging the recent progress on constrained MRSI reconstruction using learned nonlinear low-dimensional representations, we propose here a new method for SNR-enhancing reconstruction from rapidly generated, noisy J-resolved data, that can computationally efficiently enforce an accurate nonlinear low-dimensional representation of high-dimensional J-resolved spectroscopic signals through a learned network-based project as well as complementary spatial constraints. The proposed method has been shown to improve the SNR significantly for in vivo J-resolved 1H-MRSI of the brain.
Introduction
J-resolved 1H-MRSI offers improved quantification of spectrally overlapping molecules and the ability to map metabolite relaxation parameters1. However, the need to acquire data at multiple TEs inevitably increases the imaging time. Fast sequences can accelerate data acquisition but often at the expense of SNR2-6 F.urthermore, data at longer TEs suffer more from SNR loss. Low-dimensional modeling based reconstruction methods have shown great potential in enabling better speed and SNR tradeoffs for J-resolved MRSI7-10. Building on the recent progress on constrained MRSI reconstruction using learned nonlinear low-dimensional representations, we propose here a new method for SNR-enhancing reconstruction from rapidly generated, noisy J-resolved data. Our method, called RAIISE (joint leaRning of nonlineAr representatIon and projectIon for faSt constrained MRSI rEconstruction), effectively enforces an accurate nonlinear low-dimensional representation of high-dimensional J-resolved spectroscopic signals through a learned network-based projector, integrating with a complementary spatial constraint in a regularized reconstruction framework. We show that RAIISE can improve the SNR significantly for in vivo J-resolved 1H-MRSI of the brain with highly efficient computation.Theory and Method
JMRSI Reconstruction using RAIISE
The key feature of RAIISE is to jointly learn a nonlinear low-dimensional representation of high-dimensional spectroscopic signals and a projector to effectively recover the low-dimensional embeddings, integrated into a formulation and fast algorithm that also considers the forward encoding model spatial constraint and enforces the low-dimensional model in a highly computational efficient way. More details on RAIISE and the related training strategies are provided in a concurrently submitted abstract. The key contribution of this work is adapting RAIISE to achieve SNR-enhancing reconstruction from noisy J-resolved MRSI data. Specifically, to handle the high-dimensional multi-TE FIDs for J-resolved MRSI, we used a deep complex-valued convolutional autoencoder structure (DCCAE) described in [11] for the encoder and projector in RAIISE. This allows us to process data acquired at an arbitrary number of TEs in a highly scalable fashion compared to the fully connected structure8,10. The projector was trained with simulated noisy signals at various SNRs, generated by adding different noise realizations to the clear training data.
With the trained projector, RAIISE-based reconstruction from experimental J-resolved MRSI data can be formulated as
$$
\hat{\mathbf{S}}=\arg{\min_{{\mathbf{S}\in D}\left(\mathbf{L}\right)}{||d-\mathcal{F}_\Omega\left\{\mathbf{B}\odot\mathbf{S}\right\}||_2^2}}+\lambda||\mathbf{D}_w{\mathbf{S}}||_1\ \ \left(1\right)
$$
where $$$D$$$ is the decoder with a corresponding low-dimensional embedding $$$\mathbf{L}$$$, $$$d$$$ denotes the noisy multi-TE (k, t)-space measurement, $$$\mathbf{B}$$$ models B0 inhomogeneity effects, and $$$\mathcal{F}_\Omega$$$ an encoding operator. A weighted-l1 constraint, i.e., $$$|\mathbf{D}_w{\mathbf{S}}||_1$$$ was used in this work, where $$$\mathbf{D}_w$$$ is a weighted finite-difference operator. Finally, an algorithm combing alternating-direction-method-of-multipliers (ADMM) with a fast projection gradient decent algorithm12 was developed to efficiently solve the above problem (algorithm details can be found in the concurrently submitted abstract).
Data Acquisition
We evaluated the proposed method with different J-resolved MRSI acquisitions. All data were generated by the fast multi-TE sequence14 with both 3D and 2D data on a 3T Siemens Prisma scanner and a 20-channel head coil. All studies were IRB approved. For the 3D data, the acquisition parameters are =: TR/TE = 1000/ [65, 95, 125, 155, 185, 215] ms (6 TEs), FOV=220*220*64 mm3, matrix size=32*32*8, spectral bandwidth = 1250 Hz and 320 gradient echoes in each EPSI readout. The total acquisition took about 20 minutes. For the 2D data, the parameters are: TR/TE = 1100/ [30, 50, 70, 90, 110, 130, 150, 170, 190, 210, 230, 250] ms (12 TEs to demonstrate the flexibility and scalability of the proposed method), FOV = 220*220 mm2, slice thickness = 15 mm, matrix size = 32*32, and same bandwidth and echo numbers. The acquisition time was ~22 minutes with 3 averages. Weak water suppression and 6 OVS bands were used. Nuisance signals were first removed before reconstruction14.
Results
Figure 1 shows a set of spatially-resolved spectra from the 3D scan for the noisy and the denoised data produced by the proposed RAIISE reconstruction (Denoised). Significant SNR improvement can be observed with the denoised data showing clear T2 decays not observable in the noisy data. The total reconstruction time was only ~25 mins. The estimated metabolite maps were shown in Fig. 2. As can be seen, the proposed method yielded clear SNR enhancement, and better GW/WM/CSF contrast, especially for the J-coupled molecules. Figure 3 compares the reconstruction results (both metabolite maps and voxel spectra) from the 2D scan with a single average (~7.3min scan). Impressive improvement in spatiospectral data quality can be seen, especially in the J-resolved spectra. To further test the reproducibility of the method, we created artificial repeat scans through different averages, i.e., scan1: average1&2; scan2: average2&3. Figure 4 shows the Bland-Altman plot of the quantification results, and the proposed method achieved notable variance reduction and higher scan-to-scan consistency.Conclusion
We reported a new computationally efficient method for SNR-enhancing reconstruction from rapidly generated, noisy J-resolved 1H-MRSI data. The effectiveness of the proposed method has been demonstrated using in vivo 3D and 2D J-resolved data, both qualitatively and quantitatively.Acknowledgements
This work was supported in part by NSF-CBET-1944249 and NIH-NIBIB-1R21EB029076A.References
[1] de Graaf RA. In Vivo NMR Spectroscopy: Principles and Techniques. John Wiley and Sons, 2019.
[2] Tsai SY, et al. Fast mapping of the T2 relaxation time of cerebral metabolites using proton echo‐planar spectroscopic imaging (PEPSI). MRM, 2007;57:859-65.
[3] Wilson NE, et al. Accelerated five‐dimensional echo planar J‐resolved spectroscopic imaging: implementation and pilot validation in human brain. MRM, 2016;75:42-51.
[4] Sarma MK, et al. Echo-planar J-resolved spectroscopic imaging using dual read-outs: implementation and quantitation of human brain metabolites. Sci Rep, 2017;7:1-1.
[5] Adalsteinsson E, et al. Spatially resolved two‐dimensional spectroscopy. MRM, 1999;41:8-12.
[6] Andronesi OC, et al. Correlation chemical shift imaging with low‐power adiabatic pulses and constant‐density spiral trajectories. NMR Biomed, 2012;25:195-209.
[7] Tang L, et al. Accelerated J‐resolved 1H‐MRSI with limited and sparse sampling of (k, t1, t2) ‐space. Magn Reson in Med, 2019; 85: 30-41.
[8] Lam F, et al. Constrained magnetic resonance spectroscopic imaging by learning nonlinear low-dimensional models. IEEE Trans Med Imaging, 2020;39:545-555.
[9] Li Y, et al. SNR-enhancing reconstruction for multi-TE MRSI using a learned nonlinear low-dimensional model. In Proc of ISMRM, 2021;p.1998.
[10] Li Y, et al. Separation of metabolites and macromolecules for short-TE 1H-MRSI using learned component-specific representations. IEEE-TMI, 2021;40:1157-1167.
[11] Trabelsi C, et al. Deep complex networks. ICLR 2018.
[12] Gupta H, et al., CNN-based projected gradient descent for consistent CT image reconstruction. IEEE-TMI, 2018; 37:1440-1453.
[13] Wang Z, et al. High-resolution, 3D multi-TE 1H-MRSI using fast spatiospectral encoding and subspace imaging. MRM, 2021, In Press.
[14] Ma C, et al. Removal of nuisance signals from limited and sparse 1H MRSI data using a union‐of‐subspaces model. MRM, 2016;75:488-97.
Figures
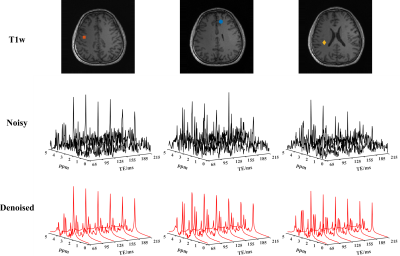
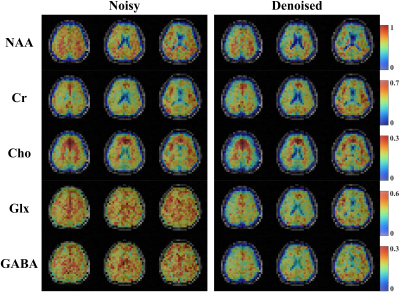
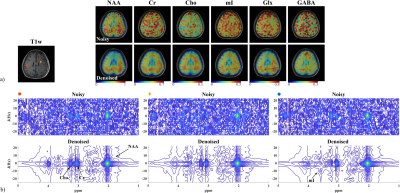
Figure 3 Results from the multi-averaged 2D scan: a) Anatomical image (T1w) as well as the fitted metabolite maps for NAA, Cr, Cho, mI, Glx, and GABA (zero-padded to the anatomical image resolution). The noisy and denoised results are shown in the first and second row; b) 2D J-resolved spectra from different voxels with locations marked in a (a) comparing the noisy (top) and the denoised (bottom) data. The TE dimension (t1) was zero padded from 12 to 20. Significantly better metabolite maps and SNR enhancement can be observed, especially in the 2D spectra.

Figure 4 Bland-Altman experiments on two repeat scan testing the reproducibility of the proposed method. We can see that the proposed methods achieved a substantial variance reduction compared to the noisy measurements, especially for the J-coupled molecules (e.g., mI, Glx), as indicated by the scatter plots and reproducibility coefficient (RPC).