3553
Two-pool model with exchange is more sensitive to exchange increases during apoptosis than the partially absorbing wall model
Daniel Djayakarsana1, Greg Stanisz1, and Colleen Bailey1
1Sunnybrook Research Institute, Toronto, ON, Canada
1Sunnybrook Research Institute, Toronto, ON, Canada
Synopsis
Modeling diffusion that incorporates the microscopic partially absorbing wall is a more realistic description compared to the standard Bloch equation based two-site model with exchange. The resulting signal equations are more complex and involve working in the Laplace domain. Here, we demonstrate that the increased spatial relevance of the partially absorbing wall model does not improve fitting in our AML model treated with cisplatin for cell death. In fact, the partially absorbing wall model fits and parameters are poorer. Therefore, extracting diffusion parameters from the Bloch equation based two-site exchange model is sufficient for our diffusion MRI datasets.
Introduction
Microstructural changes due to cancer treatments are prevalent before macrostructural size changes1. More complex modeling may be more sensitive to these changes but requires additional data or challenges hardware limitations. Here, we analyze the time-dependent diffusion signal using two different models: a two-pool model with exchange that assumes well-mixed pools, and a two-pool model that incorporates spin starting location into the boundary conditions using a “partially absorbing wall” assumption. Model parameters, including water exchange and intracellular fraction, are examined following induction of cell death.Methods
An acute myeloid leukemia cell line (AML-5) was cultured in suspension with alpha-MEM, FBS and penicillin/streptomycin. Apoptosis was induced with 10 μg/mL of cisplatin for 36 hours. Control cells were untreated. Each group was centrifuged at 2400 g to pack the cells into a pellet. Approximately 1x109 cells were used in each NMR tube. Five biological replicates were performed.A 7T vertical small bore Bruker scanner was used with a 40/30 mm quadrature receive and transmit coil. Diffusion was quantified with DTI-STEAM-EPI (1 direction, 7 b-values=0-5000s/mm2, TE/TR=35ms/1.5s, 7 mixing times TM=6.7-233ms).
Diffusion was fitted with two different models: a two-pool partially absorbing wall2 and a Bloch equation-based model of water exchange between two pools3. For both models, one pool is a spherical intracellular pool with a single radius and an extracellular pool. We assume the spin density for both the intracellular and extracellular pools are equivalent so that the water fractions and volume fractions are the same. Fit uncertainty was calculated using the Akaike information criterion (AIC) to compensate for the different number of parameters.
After MRI, cells were fixed in 10% formalin for at least two weeks before histological processing and staining with haematoxylin and eosin (H&E).
Results
Fits using the partially absorbing wall model were noticeably poorer than the Bloch equation model (Figure 1). The fit parameters from the Bloch equation model also had smaller confidence intervals for more parameters (Figure 2).The intracellular water fraction showed a significant decrease in both models, while the water exchange only increased for the Bloch equation model. The radius did not show a significant change for either model (Figure 3).
Histology demonstrates the morphological changes due to apoptosis, as well as the variation between experiments (Figure 4).
Discussion/Conclusion
The intracellular fraction for the control for the partially absorbing wall and Bloch equation model (0.6 ± 0.2 and 0.77 ± 0.08, respectively) is within the range of the theoretical value for close randomly packed spheres, which is around 0.64, but the partially absorbing wall model shows a larger range between biological replicates. Similarly, the radius in the control group (4.4 ± 0.7 µm and 5.1 ± 0.3, respectively) was in the expected range of 5 microns with the partially absorbing wall model having a larger variation. The intracellular water exchange rate (6 ± 7 s-1 and 4.9 ± 0.9 s-1, respectively) is higher than previous findings in AML cells measured with relaxation methods4 but in line with higher exchange values that have been measured in HeLa cells5.In the apoptotic group, both models demonstrated a decrease in intracellular fraction (0.36 ± 0.09 and 0.5 ± 0.1, respectively), which is expected as the cells begin to shrink and thus lose intracellular volume. For the partially absorbing wall model the water exchange does not significantly change, while the Bloch equation model demonstrates a significant increase in the water exchange (4 ± 2 s-1 and 10 ± 3 s-1, respectively). We expect the water exchange to increase due to the increased surface area to volume from blebbing and increased membrane permeability and from previous experiment in AML cells demonstrating increased exchange 36 hours after cisplatin treatment4. The radius does not show a significant change in either model (5 ± 2 µm and 5.2 ± 0.7 µm, respectively), whereas we would expect the radius to decrease as cells shrink during apoptosis. This could be due to morphological variations seen in the histology or the inaccuracy of modelling the complex membrane blebbing and apoptotic process as spherical cells with identical radii.
The values for the intracellular fraction in both models and both groups are lower than previous findings4 due to limitation of only fitting a single sphere size. With different sizes and shapes, especially in the apoptotic group, the packing would be increased and thus have a greater intracellular fraction.
The partially absorbing wall model might be expected to better describe the data than the Bloch equation model as the partially absorbing wall model incorporates the initial location of the spins. Our fitting of the diffusion data shows the converse. Here, we used the Talbot inversion method as it provided more stable parameter values relative to the Gaver-Stehfest inversion method. Unfortunately, the change in inversion method did not improve the fits.
Both models were sensitive to intracellular fraction while the Bloch equation model was also sensitive towards water exchange. Therefore, the Bloch equation model is sufficiently sensitive to microscopic cell death for realistically attainable diffusion MRI scan parameters. Future work will extend this method in vivo and investigate the inconsistencies of the partially absorbing wall model.
Acknowledgements
We would like to acknowledge MRI protocols and assistance from Wilfred Lam and Ryan Oglesby; Anoja Giles for help with cell culture and Gregory Czarnota for access to their lab space and materials. Funding/support provided by Natural Sciences and Engineering Research Council of Canada.References
- Arruebo M, Vilaboa N, Sáez-Gutierrez B, et al. Assessment of the Evolution of Cancer Treatment Therapies. Cancers. 2011;3(3):3279-3330. doi:10.3390/cancers3033279
- Price WS, Barzykin AV, Hayamizu K, Tachiya M. A Model for Diffusive Transport through a Spherical Interface Probed by Pulsed-Field Gradient NMR. Biophysical Journal. 1998;74(5):2259-2271. doi:10.1016/S0006-3495(98)77935-4
- Stanisz GJ, Li JG, Wright GA, Henkelman RM. Water dynamics in human blood via combined measurements of T2 relaxation and diffusion in the presence of gadolinium. Magn Reson Med. 1998;39(2):223-233. doi:10.1002/mrm.1910390209
- Bailey C, Giles A, Czarnota GJ, Stanisz GJ. Detection of apoptotic cell death in vitro in the presence of Gd-DTPA-BMA. Magn Reson Med. 2009;62(1):46-55. doi:10.1002/mrm.21972
- Zhao L, Kroenke CD, Song J, Piwnica-Worms D, Ackerman JJH, Neil JJ. Intracellular water-specific MR of microbead-adherent cells: the HeLa cell intracellular water exchange lifetime. NMR Biomed. 2008;21(2):159-164. doi:10.1002/nbm.1173
Figures
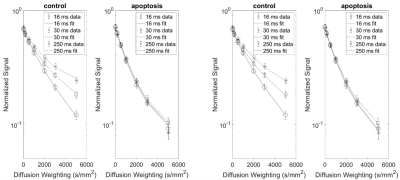
Figure 1: Partially absorbing wall (left) and Bloch equation
(right) model fits for a single dataset. Three diffusion times are shown for
clarity, but seven diffusion times were used for fitting. Error bars are
standard deviation of pixel-by-pixel variation. The AICs for the partial
absorbing wall model are 826.9 and 423.7 and the AICs for the Bloch equation
model are 579.0 and 383.0 for control and apoptosis, respectively.
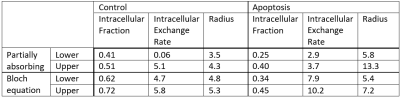
Figure 2: Table of the 95% confidence interval for the fitted
parameters of the partially absorbing wall and Bloch equation models for a
single dataset.
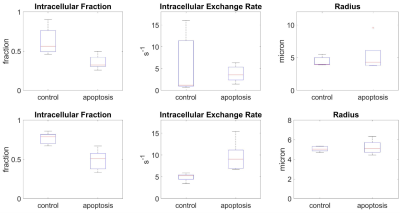
Figure 3: Parameter box plots for both the partially
absorbing wall (top) and Bloch equation (bottom) models. Red line indicates the
median and box limits the interquartile range across n=5 experiments. Whiskers
represent the range.
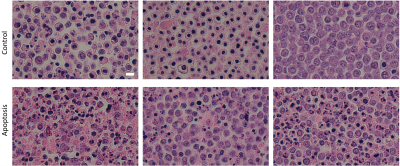
Figure 4: H&E histology slides demonstrating the
morphological changes between Control cells and cells treated with cisplatin 36
hours before experiment to induce apoptosis. Variation between biological
replicates is also evident, with each column representing a different
biological replicate. Scale bar is 10 µm and
all the images are of the same magnification.
DOI: https://doi.org/10.58530/2022/3553