3552
Intuitive Angle-Aware Bilateral Filtering Revealing Asymmetric Fiber ODF for Improved Fiber Tractography
Charles Poirier1 and Maxime Descoteaux1
1Computer Sciences, Université de Sherbrooke, Sherbrooke, QC, Canada
1Computer Sciences, Université de Sherbrooke, Sherbrooke, QC, Canada
Synopsis
Although the voxel-wise signal acquired by diffusion MRI is symmetric, it is not always the case of the underlying fiber configurations. We present angle-aware bilateral filtering, an intuitive method for denoising fiber ODF fields revealing asymmetric fiber ODFs. To evaluate the effect of the filtering, tractography is performed on the resulting asymmetric fiber ODF field. Compared to the tractogram obtained from the original fiber ODF field, we show that using asymmetric filtered fiber ODF field as input to a fiber tracking algorithm reduces the ratio of incomplete streamlines and false connections and increases the proportion of true connections.
Introduction
Due to the symmetric nature of the diffusion process, fiber orientation distribution functions1-3 (fODF) are usually defined as antipodally symmetric spherical functions (SF). However, because it is not the case for the underlying white matter (WM) fiber configurations4,5, numerous techniques have been proposed to generate asymmetric ODFs6-15. These signals, better aligned with the underlying anatomy, have been shown to improve the quality of fiber tracks reconstruction9,11,13,14. However, these methods often relie on complex mathematical constructions designed for the specific purpose of generating asymmetries. In the present work, we show that asymmetric fODF arise naturally from a simple anisotropic SF filtering. We propose an intuitive extension to bilateral filtering16, which we dub angle-aware bilateral filtering, revealing asymmetric fODF as a result of filtering a symmetric fODF field. Furthermore, we show that tracking on the resulting signals increases the ratio of valid streamlines while significantly reducing the proportion of incomplete streamlines.Methods
I. Bilateral filteringThe bilateral filter uses a combination of Gaussians for domain and range filtering. Because fODF are defined in the 5-dimensional (5D) spatio-angular domain, we extend bilateral filtering to consider the variation in angle between the sampled fODF directions and the directions to neighbour voxels by adding a third Gaussian distribution for angular domain filtering (figure 1). Formally, the filtered fODF $$$\phi'(x, u)$$$ for voxel $$$x$$$ and unit direction $$$u$$$ is given by
$$
\phi'(x, u) = \frac{1}{W(x, u)}\sum_{y \in N(x)} G_{\sigma_{spatial}}(||y - x||)\cdot G_{\sigma_{angular}}\left(\arccos(u\cdot\frac{y - x}{||y - x||})\right)\cdot G_{\sigma_{range}}(|\phi(x, u) - \phi(y,u)|)\cdot \phi(x,u),
$$
where $$$N(x)$$$ is the set of neighbours of $$$x$$$, $$$G_{\sigma}$$$ is the normal distribution of standard deviation $$$\sigma$$$ and $$$\phi(x, u)$$$ is the input fODF. The resulting SF is not restricted to being antipodally symmetric and can be expressed in a full SH basis (available in DIPY17) to preserve the asymmetries arising from the filtering.
II. Asymmetric tracking
For tracking on asymmetric fODF, we use an in-house local tracking implementation. In comparison to the DIPY local tracking implementation, where the next direction is chosen using the absolute value of the dot product between the last tracking directions and all directions on a hemisphere, our in-house implementation chooses the next direction using the signed dot product between the last tracking direction and directions on the entire sphere.
III. Experiments
FODF of maximum SH order 8 taken from a simulated version of the FiberCup phantom18-21 are used as input to the filtering. To find the optimal set of hyperparameter values, the input signal is filtered for $$$\sigma_{range} \in \{0.5, 1.0, 1.5\}$$$, $$$\sigma_{spatial} \in \{1.0, 2.0, 3.0\}$$$ and $$$\sigma_{angular} \in \{\pi/4, \pi/2, 3\pi/4\}$$$. The filtered image is projected on both a symmetric and a full SH basis, resulting in symmetric filtered (syf) fODF and asymmetric filtered (asyf) fODF, respectively. Probabilistic tracking – with step size of 0.5 mm, maximum angle of 20 degrees and minimum SF threshold of 0.1 – is then performed on all filtered fODF from 15000 interface seeding points. A binary mask is used to constrain the tracking to the WM. Tracking is also done on the input fODF field for baseline comparison. All resulting tractograms are then evaluated5,22 in terms of true connections (TC), false connections (FC), no connections (NC) and wrong-path connections (WPC). The overlaps between reconstructed TC and ground-truth masks are also reported. The overall best set of hyperparameters is given by the highest TC ratio. To visualize the behaviour of the tracking algorithm, 1000 streamlines are generated from the same seeding point on all syf-based, asyf-based and input fODF fields.
Results and discussion
Comparing TC for all experiments shows that the best tractogram is asyf-based with hyperparameter values of $$$\sigma_{angular}=\pi/4$$$, $$$\sigma_{spatial}=2.0$$$ and $$$\sigma_{range}=0.5$$$. Figure 2 shows that asyf-based tractography increases the ratio of TC and reduces the ratio of FC and NC, resulting in denser tractograms. Indeed, after excluding NC, the asyf-based tractogram contains 9809 streamlines against 5710 and 5600 for the syf-based and baseline tractograms respectively.The bundle-wise TC overlap achieved by the best tractogram (figure 3) shows that asyf-based tracking does not systematically result in better overlaps. However, the best tractogram always has a higher amount of TC streamlines than the syf-based and baseline tractograms for each bundle (figure 4). In figure 5, the regions identified by red arrows show a lot of NC and FC in baseline and syf-based tracking, while the green arrows highlight the reduced amount of NC and FC for those same regions after asyf-based tracking. These results demonstrate that although the effect on the overlap is not significant, asyf-based tracking prevents streamlines from leaving the WM mask prematurely. Comparing the fODF glyphs, we see that neighbour fODF are better aligned following filtering and, when using a full SH basis, they display striking asymmetric patterns.
Conclusion
The use of angle-aware bilateral filtering for processing fODF, combined with a full SH basis, significantly reduces the number of incomplete streamlines for the FiberCup phantom without increasing the amount of false connections. However, testing needs to be done on more realistic data in order to better quantify the real impact of the proposed method on tractography. It would also be important to compare the proposed method to other existing techniques for generating asymmetric ODFs.Acknowledgements
This work was partly supported by the Canada Graduate Scholarships - Master's program, from the Natural Sciences and Engineering Research Council (NSERC) of Canada.References
- Tournier J-D, Calamante F, Gadian DG, Connelly A. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. NeuroImage. 2004 Nov 1;23(3):1176–85.
- Tournier J-D, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: Non-negativity constrained super-resolved spherical deconvolution. NeuroImage. 2007 May 1;35(4):1459–72.
- Descoteaux M, Deriche R, Knösche TR, Anwander A. Deterministic and probabilistic tractography based on complex fiber orientation distributions. IEEE Transactions on Medical Imaging. 2009 Feb;28(2):269–86
- Jbabdi S, Johansen-Berg H. Tractography: Where Do We Go from Here? Brain Connect. 2011 Sep;1(3):169–83.
- Maier-Hein KH, Neher PF, Houde J-C, Côté M-A, Garyfallidis E, Zhong J, et al. The challenge of mapping the human connectome based on diffusion tractography. Nat Commun. 2017 Dec;8(1):1349.
- Delputte S, Dierckx H, Fieremans E, D’Asseler Y, Achten R, Lemahieu I. Postprocessing of Brain White Matter Fiber Orientation Distribution Functions. In: 2007 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro. 2007. p. 784–7.
- Barmpoutis A, Vemuri BC, Howland D, Forder JR. Extracting Tractosemas from a Displacement Probability Field for Tractography in DW-MRI. In: Metaxas D, Axel L, Fichtinger G, Székely G, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2008. Berlin, Heidelberg: Springer; 2008. p. 9–16. (Lecture Notes in Computer Science).
- Duits R, Franken E. Left-Invariant Diffusions on the Space of Positions and Orientations and their Application to Crossing-Preserving Smoothing of HARDI images. Int J Comput Vis. 2011 May 1;92(3):231–64.
- Ehricke H-H, Otto K-M, Klose U. Regularization of bending and crossing white matter fibers in MRI Q-ball fields. Magnetic Resonance Imaging. 2011 Sep 1;29(7):916–26.
- Reisert M, Kellner E, Kiselev VG. About the Geometry of Asymmetric Fiber Orientation Distributions. IEEE Transactions on Medical Imaging. 2012 Jun;31(6):1240–9.
- Bastiani M, Cottaar M, Dikranian K, Ghosh A, Zhang H, Alexander DC, et al. Improved tractography using asymmetric fibre orientation distributions. NeuroImage. 2017 Sep 1;158:205–18.
- Cetin Karayumak S, Özarslan E, Unal G. Asymmetric Orientation Distribution Functions (AODFs) revealing intravoxel geometry in diffusion MRI. Magnetic Resonance Imaging. 2018 Jun 1;49:145–58.
- Feng Y, He J. Asymmetric fiber trajectory distribution estimation using streamline differential equation. Medical Image Analysis. 2020 Jul 1;63:101686.
- Wu Y, Hong Y, Feng Y, Shen D, Yap P-T. Mitigating gyral bias in cortical tractography via asymmetric fiber orientation distributions. Medical Image Analysis. 2020 Jan 1;59:101543
- Poirier, C., St-Onge, E., & Descoteaux, M. (2021). Investigating the occurrence of asymmetric patterns in white matter fiber orientation distribution functions. Proc. Intl. Soc. Mag. Reson. Med. (2021), 29.
- Tomasi, C., & Manduchi, R. (1998). Bilateral filtering for gray and color images. Sixth International Conference on Computer Vision (IEEE Cat. No.98CH36271), 839–846. https://doi.org/10.1109/ICCV.1998.710815
- Garyfallidis, E., Brett, M., Amirbekian, B., Rokem, A., Van Der Walt, S., Descoteaux, M., & Nimmo-Smith, I. (2014). Dipy, a library for the analysis of diffusion MRI data. Frontiers in Neuroinformatics, 8, 8. https://doi.org/10.3389/fninf.2014.00008
- Fillard, P., Descoteaux, M., Goh, A., Gouttard, S., Jeurissen, B., Malcolm, J., Ramirez-Manzanares, A., Reisert, M., Sakaie, K., Tensaouti, F., Yo, T., Mangin, J.-F., & Poupon, C. (2011). Quantitative evaluation of 10 tractography algorithms on a realistic diffusion MR phantom. NeuroImage, 56(1), 220–234. https://doi.org/10.1016/j.neuroimage.2011.01.032
- Poupon, C., Rieul, B., Kezele, I., Perrin, M., Poupon, F., & Mangin, J.-F. (2008). New diffusion phantoms dedicated to the study and validation of high-angular-resolution diffusion imaging (Hardi) models. Magnetic Resonance in Medicine, 60(6), 1276–1283. https://doi.org/10.1002/mrm.21789
- Poupon, C., Laribiere, L., Tournier, G., Bernard, J., Fournier, D., Fillard, P., Descoteaux, M., et al. (2010). A Diffusion Hardware Phantom Looking Like a Coronal Brain Slice. Proceedings of the International Society for Magnetic Resonance in Medicine.
- Neher, Peter F., et al. “Fiber Tractography Using Machine Learning.” NeuroImage, vol. 158, Sept. 2017, pp. 417–29. ScienceDirect, https://doi.org/10.1016/j.neuroimage.2017.07.028.
- Côté, M.-A., Girard, G., Boré, A., Garyfallidis, E., Houde, J.-C., & Descoteaux, M. (2013). Tractometer: Towards validation of tractography pipelines. Medical Image Analysis, 17(7), 844–857. https://doi.org/10.1016/j.media.2013.03.009
Figures
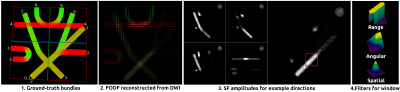
Figure 1: Visualization of the filtering algorithm. 1. Ground-truth bundles are shown for reference. 2. Input fODF image defined in the 5D spatio-angular domain. 3. SF amplitudes evaluated for example directions (shown in grey sphere). Filtering is done separately for all resulting SF images. 4. Filters for the red window. The spatial filter is uniform for all directions, the angular filter depends on the processed direction and the range filter depends on the intensities in the processed window. The colormap for the filters goes from purple (minimum value) to yellow (maximum value).
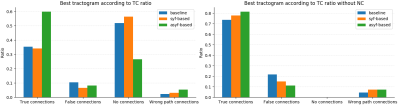
Figure 2: Best tractogram according to TC. The best tractogram was obtained from asyf fODF using $$$\sigma_{angular}=\pi/4$$$, $$$\sigma_{spatial}=2.0$$$ and $$$\sigma_{range}=0.5$$$. Left: Metrics for the best tractogram according to TC compared to its symmetric counterpart and to baseline. Right: Distribution of TC, FC and WPC after removing NC from the resulting tractograms. NC can be easily filtered out as they don't connect two grey matter regions. This bar plot shows the distribution of the remaining streamlines.
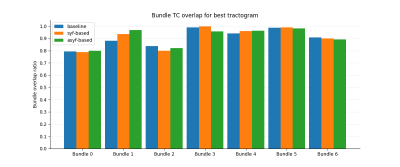
Figure 3: Bundle TC overlap for the best tractogram (asyf-based) compared to syf-based counterpart and baseline. This result suggests that syf- and asyf-based tracking does not dramatically impact bundle overlap for the FiberCup phantom for most bundles. However, for bundle 1, asyf-based tracking (96.7%) increases the overlap of approximately 8% compared to the baseline (88.2%).
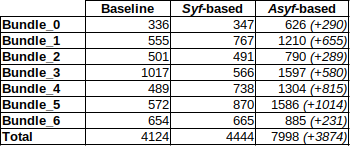
Figure 4: Number of TC streamlines per bundle for best tractogram (asyf-based) compared to syf-based and baseline tractograms. For all bundles, the asyf-based tractogram contains more TC than the other tractograms for the same number of seeding positions. The number of new streamlines compared to baseline is reported in parentheses. This result confirms that all bundles benefit from the filtering as they all increase their number of TC.
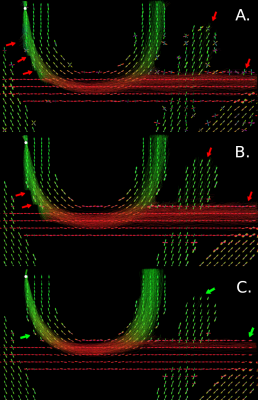
Figure 5: Tracks obtained by performing tracking from same seeding position (white dot) 1000 times for syf fODF (B.) and asyf fODF (C.) using the optimal hyperparameter values compared to input fODF (A.). Arrows highlight regions of interest where asyf-based tractography performs better than other tested methods. FODF for the middle slice of the phantom are also shown in the background. FODF shown in subfigure C. display obvious asymmetric configurations.
DOI: https://doi.org/10.58530/2022/3552