Introduction

Radial Diffusion Spectrum Imaging (RDSI) allows for estimating Orientation Distribution Functions (ODFs) with high angular precision [1]. Coupling RDSI with ODF-Fingerprinting (ODF-FP) [2] – a dictionary-based technique to reconstruct fiber directions – helps identify fibers crossing at narrow angles below 45 degrees [3]. However, the performance of RDSI heavily depends on the sampling length parameter – a multiplicative factor (specific to acquisition protocol) used in numerical integration of diffusion signal, which controls sharpness of ODFs [1] (Figure 1). Selecting an optimal sampling length is challenging and the literature offers little guidance [1,4].

In our study, we attempt to optimize sampling lengths in RDSI to maximize accuracy of reconstruction of crossing fibers. For this, we used diffusion-weighted images (DWIs) of two phantoms built with Taxon™ technology, i.e. textile water-filled tubes with 0.8-µm inside diameter that approximates the anatomical scale of axons found in the human brain [5]. Here, we characterized configurations of synthetic fibers crossing at 10, 15, 20, 30 and 45 degrees. We then tried to identify optimal sampling lengths for RDSI to be used in reconstruction of the acquired dMRI and generation of the ODF-dictionary for ODF-FP.

Our preliminary results suggest a criterion for selecting near-optimal sampling lengths. In addition, we show that the ODF-FP&RDSI combination with appropriately chosen sampling lengths reaches the average accuracy of ±10° in all studied crossing angles. This is promising for future in vivo clinical applications of these techniques. Particularly for white matter tractography in challenging regions of the human brain.

Methods

Data:
For both phantoms (Figure 2), we acquired 4-shell DWIs sampled at 60 directions (distributed on radial lines at b=250,1000,2250,4000s/mm² interleaved with 17 images at b=0) with 2x2x2mm resolution, TE/TR=74/8000ms.

Reconstruction:
We considered ODFs defined as
$$\mbox{ODF}(\mathbf{r},\theta,\phi)=\int p_{\Delta}(\mathbf{r},L\mathbf{u})L^2\,dL,$$
where $$$\mathbf{r}\in\mathbb{R}^3$$$ determines spatial location, $$$p_{\Delta}(\cdot,\cdot)$$$ is a probability distribution function associated with diffusion at $$$\mathbf{r}$$$ in the direction $$$L\mathbf{u}$$$ specified by $$$(\theta,\phi)$$$ with $$$L>0$$$ and $$$\mathbf{u}\in\mathbb{R}^3$$$ such that $$$\|\mathbf{u}\|=1$$$. Using RDSI, we approximated these ODFs as
$$\mbox{ODF}(\mathbf{r},\theta,\phi)=\int S(\mathbf{r},\mathbf{q})F_{\lambda}(\mathbf{q},\mathbf{u})\,d\mathbf{q},$$
where $$$S(\cdot,\cdot)$$$ is the dMRI signal measured at $$$\mathbf{r}$$$ with the q-space sampling direction $$$\mathbf{q}\in\mathbb{R}^3$$$ and $$$F_{\lambda}(\cdot,\cdot)$$$ is the geometric encoding matrix (introduced by Baete et al. [1]) parametrized with the sampling length $$$\lambda>0$$$ that controls sharpness of ODFs.

We used the above RDSI reconstruction twice by executing our in-house MATLAB™ implementations [6,7]. First, we calculated ODFs of the acquired dMRI. Then, we calculated ODFs of the randomly generated elements of the ODF-dictionary [8] containing 1000000 samples with 0≤N≤2 crossing fibers per voxel. In both cases, we tested multiple variants of the sampling length $$$\lambda\in\{0.1,0.2,\ldots,1.5\}$$$

Evaluation:
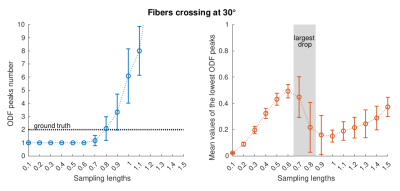
We visually inspected the shapes of ODFs obtained with various sampling lengths (both for the acquired and the generated inputs) and computed the absolute errors between the ground truth crossing angles and the angles reconstructed with ODF-FP. Based on these, we proposed the selection criterion for sampling lengths defined as the one introducing the largest drop of the value of the smallest ODF peak found with a simple local search.

Results

As we show in Figure 1, the optimal selection of sampling length in RDSI turned out to be a trade-off between blurry ODFs (low $$$\lambda$$$) and an emergence of artifacts (high $$$\lambda$$$). In our dMRI acquisition, the highest sharpness without significant artifacts was reached for the sampling lengths at approximately 0.7.

Interestingly, the ODFs computed from the noiseless, synthetically generated data (and kept in the ODF-dictionary) reached visibly higher sharpness ($$$\lambda≥1$$$) before they started producing artifacts. In result, ODF-FP successfully matched the inputs reconstructed with RDSI at $$$\lambda=0.7$$$ with the considerably sharper ODFs stored in the dictionary (Figure 3). For all crossing fibers, we observed the lowest mean reconstruction errors (below 10°) when the reconstruction sampling lengths were between 0.5 and 0.7, while the ODF-dictionary sampling schemes were at or slightly above 1.0 (Figure 4).

Moreover, the lowest reconstruction errors coincided with the accurate identification of the number of crossing fibers per voxel (i.e. 2) and the largest drop of the smallest ODF peak values (Figure 5).

Discussion

Blurring effect in ODFs decreases angular precision of fiber reconstruction [9,10]. In RDSI, this can be accounted for by maximizing the sampling length parameter up to the level where artifacts appear, which typically requires a long trial and error process.

In this work, we presented a case study of two phantoms with narrow crossing angles for which we optimized the sampling lengths in RDSI. We also showed that a use of ODF-FP can further decrease the blurring effect and improve the fiber reconstruction accuracy. Our noiseless, synthetically generated ODF-dictionaries could reach higher sampling lengths without producing artifacts. ODF-FP was able to match the ODFs from DWIs with the significantly sharper ODFs from the dictionary allowing for a relatively precise reconstruction of fibers crossing at angles as narrow as 10, 15, and 20 degrees.

Our preliminary results allowed us to propose a criterion for selecting near-optimal sampling lengths. This criterion – whether used as a default setting or as an educated guess – may accelerate and simplify the application of ODF-FP&RDSI. Future study should address in vivo imaging and the impact of factors like signal to noise ratio or voxel dimensions.

Acknowledgements

This project is supported in part by the National Institutes of Health (NIH, R01-EB028774 and R01-NS082436). This work was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R, https://www.cai2r.net), a NIBIB Biomedical Technology Resource Center (NIH P41-EB017183).