3547
Effect of Static Background Gradients on Diffusion Contrast Near Large Metallic Implants1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States, 3Bioengineering, Stanford University, Stanford, CA, United States
Synopsis
Metallic implants create severe off-resonance adjacent to the implant, in the range of 2-20 kHz at 3T. The off-resonance pattern creates a static, “always on” background gradient with unknown amplitude and polarity. Static non-linear background gradients are a known source of local encoding errors, but their effect on diffusion contrast near implants has not yet been evaluated. Static background gradients are distinct from diffusion gradient non-linearities, which affect the achieved b-value if sufficiently large. We apply theoretical results and phantom experiments to evaluate two different diffusion encoding schemes and evaluate the effect of metal-induced off-resonance on ADC quantification.
Introduction
Diffusion weighted imaging is a desirable contrast to highlight inflammation and cancer. A method for obtaining diffusion weighted images near metallic implants was recently developed by Koch et al.1 Static non-linear background gradients caused by off-resonance (1-20 kHz at 3T) near the metal implant are a known source of local encoding errors, but their effect on diffusion contrast near large implants has not yet been evaluated. Static background gradients are distinct from diffusion gradient non-linearities. Prior NMR work2 characterized interactions between static background gradients and diffusion weighting, and proposed methods for mitigating effects on quantitative apparent diffusion coefficient (ADC) estimates.Instead of the 2D, monopolar diffusion encoding, DW-MSI split-blade PROPELLER1 developed by Koch et al, we employed a 3D, twice-refocused stimulated echo diffusion prepared Cartesian Fast Spin Echo sequence3 (Figure 1A) to correct non-CPMG effects and off-resonance induced distortion from the implant4. 3D encoding improves SNR efficiency and reduces scan times.
Theory
The effect of static background gradients was known empirically in early NMR diffusion work5. It is a spatially varying, "always-on" gradient with unknown amplitude and polarity that is proportional to field strength. The background gradient increases or decreases the amplitude of the applied diffusion gradient (Figure 1B) and changes the achieved b-value. An analysis of interactions between background gradients and diffusion weighting was introduced in2.Diffusion-related attenuation including background gradients is given by:
$$b=\int_{0}^{T_{diff}}F_{diff}(t)^2+2F_{bg}(t)F_{diff}(t)+F_{bg}(t)^2dt$$
where $$$F_{diff}(t)=\int_{0}^{t}g_{diff}(\tau)d\tau$$$, $$$g_{diff}(\tau)$$$ is the applied diffusion gradient. $$$F_{bg}(t)$$$ is calculated the same way and results from the background gradient. $$$F_{diff}(t)^2$$$ is the known and desired contribution to b-value, and $$$F_{bg}(t)^2$$$ is cancelled after division by the b=0$$$\,$$$s/mm2 image. This leaves the cross-term $$$F_{bg}(t)F_{diff}(t)$$$.
$$$F_{bg}(t)$$$ and $$$F_{diff}(t)$$$ are shown for twice-refocused M0 and M1-nulled waveforms in Figure 2. $$$F_{bg}(t)$$$ is an odd function. For twice-refocused M0 diffusion encoding, $$$F_{diff}(t)$$$ is even, so the inner product:
$$\int_{0}^{T_{diff}}F_{bg}(t)F_{diff}(t)dt$$
and contribution to b-value is zero. For twice-refocused M1-nulled diffusion encoding, $$$F_{diff}(t)$$$ is odd, so the inner product with $$$F_{bg}(t)$$$ depends on gradient polarity and increases or decreases the obtained b-value, affecting ADC quantification. Diffusion encoding schemes that are insensitive to background gradients are not unique and single-refocused options exist. The effect of background gradient cannot be removed from the diffusion weighted image, similar to T1 or T2 "shine-through". Geometric averaging of opposite diffusion encoding polarities can also eliminate the cross-term6, but this doubles scan time, which is already extended due to the image encoding requirement from metal4.
Methods
The ability to quantify diffusion weighting in the presence of metal was tested at room temperature in a diffusion phantom consisting of vials with varying concentrations of H2O dissolved in acetone7. Acquisitions were performed at 3T (Signa Premier, GE Healthcare) with refocusing flip angle 120° and diffusion gradients designed with 50$$$\,$$$mT/m per axis amplitude, 40$$$\,$$$T/m/s slew rate.Acetone vials were arranged annularly around the CoCr femoral head of a total hip arthroplasty. This phantom allows for easy removal of the implant head to compare ADCs with and without metal-induced off-resonance. Scan parameters were: 2×2×5 mm voxels, b-value$$$\,$$$500 s/mm2, 24 bins, bin bandwidth 1.5 kHz, ETL 24. Mean ADC values obtained with and without metal were compared using linear regression analysis.
To demonstrate the sensitivity of ADC to static background gradients from metal, we acquired DW-MSI using twice-refocused M0 and M1-nulled waveforms with two diffusion encoding polarities. The second direction negated the amplitude of all diffusion gradients, which would ideally yield similar ADC maps since acetone-H2O exhibits isotropic Gaussian diffusion7.
Results
DW-MSI images and ADC maps obtained with and without metal in the acetone diffusion phantom are shown in Figure 3. Twice-refocused, M0-nulled diffusion encoding is insensitive to background gradients. Regression analysis between mean ADCs in each vial with and without metal gave the following linear fit:ADCwith$$$\,$$$metal=$$$\,$$$0.945·ADCno$$$\,$$$metal$$$\,$$$+$$$\,$$$0.05$$$\,$$$×$$$\,$$$10-3$$$\,$$$mm2/s, R2$$$\,$$$=$$$\,$$$0.97 , p$$$\,$$$<$$$\,$$$0.001.
While background gradients affect diffusion weighting in the b$$$\,$$$=$$$\,$$$0 s/mm2 image, the net effect after computing SDWI/Sb0 is zero. This is evident by the excellent ADC correspondence between H2O millimeters away from the implant and reference H2O vials.
From Figure 4, background gradients cause different ADC estimates with different diffusion polarities for the twice-refocused M1-nulled diffusion encoding since the cross-term $$$F_{bg}(t)F_{diff}(t)$$$ is non-zero. ADC values obtained with M1-nulled waveforms deviate in regions with rapid field variation whereas ADCs obtained with M0-nulled waveforms are unchanged.
Discussion
We demonstrated that ADC values obtained with a twice-refocused M0-nulled scheme are not affected by background gradient, but a twice-refocused M1-nulled waveform (and hence monopolar pulsed gradient spin-echo) exhibits large ADC deviations adjacent to the metal.The magnitude of the background gradient is dependent on field strength, implant material, and geometry. From Figure 4, the background gradient near the implant can reach 3-5$$$\,$$$G/cm, on the order of applied diffusion gradients. Simulations of the background gradient created by a titanium total hip replacement at 3T (Figure 5), indicate that the magnitude of the background gradient’s linear component is negligible a few centimeters from the implant. For smaller metallic hardware or acquisitions where spectral coverage is not sufficient to excite spins adjacent to the implant, the background gradient is negligible8 and unlikely to affect diagnosis.
Conclusion
Twice-refocused, M0-nulled diffusion encoding is insensitive to static background gradients from metal that affect ADC quantification.Acknowledgements
GE Healthcare. R01 EB017739 . R01 AR077706.References
1. Koch KM, Bhave S, Gaddipati A, Hargreaves BA, Gui D, Peters R, et al. Multispectral diffusion-weighted imaging near metal implants. Magnetic Resonance in Medicine 2018;79(2):987–993.
2. David Williams W, Seymour EFW, Cotts RM. A pulsed-gradient multiple-spin-echo NMR technique for measuring diffusion in the presence of background magnetic field gradients. Journal of Magnetic Resonance 1978;31(2):271–282.
3. Zhang Q, Coolen BF, Versluis MJ, Strijkers GJ, Nederveen AJ. Diffusion-prepared stimulated-echo turbo spin echo (DPsti- TSE): An eddy current-insensitive sequence for three-dimensional high-resolution and undistorted diffusion-weighted imaging. NMR in Biomedicine 2017;30(7):e3719.
4. Lu W, Pauly KB, Gold GE, Pauly JM, Hargreaves BA. SEMAC: Slice encoding for metal artifact correction in MRI. Magnetic Resonance in Medicine 2009 jul;62(1):66–76.
5. Packer KJ, Rees C, Tomlinson DJ. A modification of the pulsed magnetic field-gradient spin echo method of studying diffusion. Molecular Physics 1970;18(3):421–423.
6. Gullmar D, Haueisen J, Reichenbach RJ. Analysis of b-value Calculations in Diffusion Weighted and Diffusion Tensor Imaging. Concepts in Magnetic Resonance 2005;25A(1):53-66.
7. Wang X, Reeder SB, Hernando D. An acetone-based phantom for quantitative diffusion MRI. Journal of Magnetic Resonance Imaging 2017;46(6):1683–1692.
8. Arpinar VE, Cohen AD, Bhave S, Koch KM. Quantitative accuracy of diffusion-weighted imaging techniques as a function of susceptibility artifact resilience. In: Proceedings of the 30th Annual Meeting of ISMRM, 2021. p. 1340.
Figures
Figure 1: A) Stimulated echo diffusion preparation that corrects non-CPMG artifacts. Dephasing prior to tipup ensures uniform signal is returned to the longitudinal axis, regardless of phase from bulk motion. View Angle Tilting (VAT) gradients are applied during readout to reduce in-plane distortion as in most selective MSI methods. B) Net effect of background gradient on applied diffusion gradient.
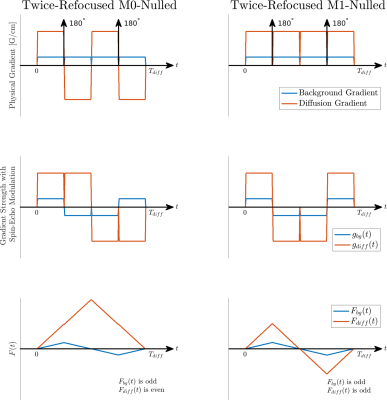
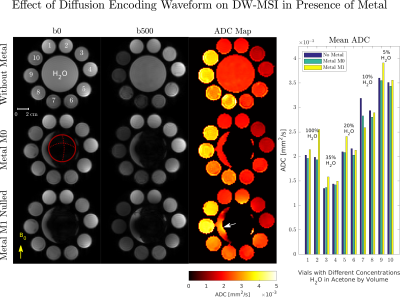
Figure 3: Acetone diffusion phantom experiment with and without metal. The red circle indicates the location of the implant. Left: ADC maps computed from b500 images obtained with M1-nulled diffusion encoding deviate from the no-metal and M0-nulled ADC maps in regions with high background field variation. This is evident in H2O directly adjacent to the implant (white arrow). Right: Mean ADCs with M1-nulled diffusion encoding have large deviations from mean ADCs obtained without metal, and with metal using the M0-nulled diffusion encoding.
Figure 4: Left: Effect of diffusion gradient polarity on ADC maps. M1-nulled encoding with diffusion gradients played on all axes exhibits anisotropy near the metal in regions with rapid background field variation. Middle: In-plane fieldmap estimated from spectral bin data. Right: Fixed slice at different spectral offsets used to calculate field map.
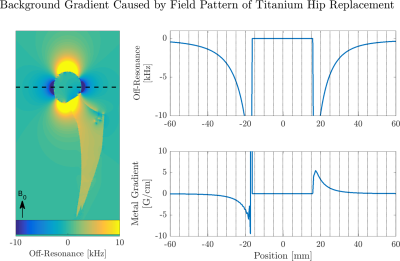
Figure 5: Left: Field pattern from convolving a dipole pattern with the susceptibility map of a titanium hip replacement at 3T. Top Right: 1D profile of off-resonance along dashed black line. Bottom Right: Resulting local gradient computed with finite differences and expressed in [G/cm]. In regions less than 1 cm from the implant, the gradient from off-resonance is on the order of the diffusion gradients (3-5 G/cm) and can affect the achieved b-value in that voxel. This effect is negligible when the distance from the implant is greater than 2 cm.