3533
Robust Low-rank Denoising of MRSI Data
Wen Jin1,2, Yibo Zhao1,2, Rong Guo1,2, Yudu Li1,2, Jie Luo3, Yao Li3, and Zhi-Pei Liang1,2
1Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 2Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 3School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China
1Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 2Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 3School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China
Synopsis
With the increasing use of MRSI in research and clinical applications, we have seen a surge in the use of low-rank models for denoising MRSI data. This paper presents a novel method for robust denoising of MRSI data corrupted by both Gaussian noise and nuisance signals. The proposed method has been validated using both simulated and in vivo data, producing impressive results. This method will further enhance the practical utility of low-rank denoising.
Introduction
MRSI has many potential research and clinical applications, but its potential has not yet been fully utilized due to low SNR1,2. To address this problem, several denoising methods have been proposed, such as low-pass filtering method and wavelet denoising method3,4. With the advent of high-performance computing, more advanced denoising methods have been proposed in recent years, one of which is low-rank denoising5–7. Low-rank denoising methods exploit the partial separability and linear predictability of MRSI signals to remove noise. The existing low-rank denoising methods are based on principal component analysis (PCA), which is optimal in removing Gaussian noise. In practice, MRSI data, especially 1H-MRSI data, are often corrupted by both Gaussian noise and outliers (e.g., nuisance signals from residual water and lipids)8. In this case, the existing low-rank denoising methods are not robust. In this paper, we propose a novel method for robust low-rank denoising of MRSI data that can effectively handle both Gaussian noise and nuisance signals. The proposed method extends the low-rank model with a new component that captures outliers. The proposed method has been validated on both simulated and in vivo data, producing impressive results.Methods
We extended the low-rank model by explicitly including an outlier component. More specifically, we expressed the measured spatiotemporal function $$$\rho(\boldsymbol{x},t)$$$ as follows:$$\rho(\boldsymbol{x},t)=\sum_{\ell=1}^L c_\ell(\boldsymbol{x})v_\ell(t)+s(\boldsymbol{x},t)+\epsilon(\boldsymbol{x},t), \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ [1]$$
where $$$\sum_{\ell=1}^L c_\ell(\boldsymbol{x})v_\ell(t)$$$ denotes the conventional low-rank model of the desired metabolite signals with temporal bases $$$\{ v_\ell(t) \}_{\ell=1}^L$$$, $$$s(\boldsymbol{x},t)$$$ represents outliers, and $$$\epsilon(\boldsymbol{x},t)$$$ denotes complex Gaussian noise. In current practice, $$$s(\boldsymbol{x},t)$$$ is assumed to be negligible and $$$\{ v_\ell(t) \}_{\ell=1}^L$$$ are determined either from the data to be denoised or from training data9. In both cases, including an outlier component, $$$s(\boldsymbol{x},t)$$$, is beneficial for improving the effectiveness and robustness of low-rank denoising.
Rewriting the signal model in Eq. (1) in matrix form, we have $$$\boldsymbol{P}=\boldsymbol{CV}+\boldsymbol{S}+\boldsymbol{E}$$$, where $$$\boldsymbol{P}$$$, $$$\boldsymbol{C}$$$, $$$\boldsymbol{V}$$$, $$$\boldsymbol{S}$$$, and $$$\boldsymbol{E}$$$ are the matrix representations of $$$\rho(\boldsymbol{x},t)$$$, $$$\{ c_\ell(\boldsymbol{x}) \}_{\ell=1}^L$$$, $$$\{ v_\ell(t) \}_{\ell=1}^L$$$, $$$s(\boldsymbol{x},t)$$$, and $$$\epsilon(\boldsymbol{x},t)$$$, respectively. Solution of $$$\boldsymbol{C}$$$, $$$\boldsymbol{V}$$$, and $$$\boldsymbol{S}$$$ under the assumption that $$$\boldsymbol{E}$$$ is a Gaussian random matrix is not unique. In this work, a sparsity constraint was imposed on $$$\boldsymbol{S}$$$, i.e., the outliers are assumed to be sparse in the spatial-spectral domain. This assumption is valid for various applications, especially for 1H-MRSI data that may contain localized residual water/lipid signals. Under this assumption, solution of the robust low-rank denoising problem can be obtained by solving the following optimization function:
$$arg min_{\boldsymbol{C},\boldsymbol{V},\boldsymbol{S}} ||\boldsymbol{P}-(\boldsymbol{C}\boldsymbol{V}+\boldsymbol{S})||^2_F+\lambda||\mathcal{F}_t\boldsymbol{S}||_1, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ [2]$$
where $$$\mathcal{F}_t$$$ represents the Fourier transformation along time. This optimization problem can be solved effectively using the popular Robust PCA algorithm that alternatively finds the low-rank component $$$\boldsymbol{CV}$$$ using singular value thresholding or conjugate gradient algorithm, and the sparse component $$$\boldsymbol{S}$$$ using soft-thresholding10. The temporal bases $$$\{ v_\ell(t) \}_{\ell=1}^L$$$ could be pre-determined from training data, then only $$$\boldsymbol{C}$$$ and $$$\boldsymbol{S}$$$ need to be solved and additional constraints such as spatial smoothness and prior probabilistic distribution can be imposed on $$$\boldsymbol{C}$$$.
Results
Simulation data were generated by adding noise and lipid signals to the ground truth metabolite signals. Figure 1 shows a comparison between the estimated basis functions from nuisance-corrupted data directly and from the low-rank component of our proposed method. As can be seen, the basis function estimated from the nuisance-corrupted data contained a significant contribution from lipid signals, which would severely degrade the performance of low-rank denoising methods. Our proposed method showed no lipid contamination on the estimated basis.Figure 2 shows the simulation results comparing our proposed method with the PCA-based low-rank denoising method. As can be seen, the proposed method not only significantly reduced the noise level but also protected the denoised metabolite signals from the contamination of lipid signals.
Table 1 shows the Monte-Carlo simulation results using the same simulation setup with 50 trials. The results demonstrated the quantitative reduction of nuisance-introduced bias in metabolite concentrations using the proposed method.
A set of in vivo brain 1H MRSI data was acquired from a healthy volunteer on a 3T Siemens Prisma scanner using an EPSI sequence with no lipid suppression. There were still some lipid residues after lipid removal, and the proposed method was used to recover metabolite signals from the data. As shown in Fig. 3, the proposed method successfully separated the metabolite signals from the lipid residues and improved the SNR of the metabolite signals.
Conclusions
We proposed a novel method for robust denoising that can effectively handle both Gaussian noise and nuisance signals. The proposed method was validated using simulated and in vivo data, producing robust denoising results from low-SNR and nuisance-corrupted MRSI data. This new method is expected to further enhance the practical utility of the low-rank denoising method.Acknowledgements
No acknowledgement found.References
1. Posse S, Otazo R, Dager SR, Alger J. MR spectroscopic imaging: principles and recent advances. J Magn Reson Imaging. 2013;37(6):1301-1325.2. Bogner W, Otazo R, Henning A. Accelerated MR spectroscopic imaging—a review of current and emerging techniques. NMR Biomed. 2021;34(5):1-32.
3. Cancino-De-Greiff HF, Ramos-Garcia R, Lorenzo-Ginori J V. Signal de-noising in magnetic resonance spectroscopy using wavelet transforms. Concepts Magn Reson. 2002;14(6):388-401.
4. Ahmed OA. New denoising scheme for magnetic resonance spectroscopy signals. IEEE Trans Med Imaging. 2005;24(6):809-816.
5. Nguyen HM, Peng X, Do MN, Liang Z-P. Denoising MR spectroscopic imaging data with low-rank approximations. IEEE Trans Biomed Eng. 2013;60(1):78-89.
6. Abdoli A, Stoyanova R, Maudsley AA. Denoising of MR spectroscopic imaging data using statistical selection of principal components. MAGMA. 2016;29(6):811-822.
7. Froeling M, Prompers JJ, Klomp DWJ, van der Velden TA. PCA denoising and Wiener deconvolution of 31P 3D CSI data to enhance effective SNR and improve point spread function. Magn Reson Med. 2021;85(6):2992-3009.
8. Ma C, Lam F, Johnson CL, Liang Z-P. Removal of nuisance signals from limited and sparse 1H MRSI data using a union-of-subspaces model. Magn Reson Med. 2016;75(2):488-497.
9. Chen Y, Li Y, Xu Z. Improved low-rank filtering of MR spectroscopic imaging data with pre-learnt subspace and spatial constraints. IEEE Trans Biomed Eng. 2020;67(8):2381-2388.
10. Candès EJ, Li X, Ma Y, Wright J. Robust principal component analysis? Journal of the ACM. 2011;58(3).
Figures
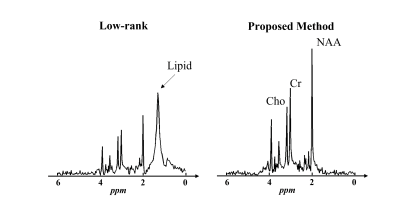
Figure
1: Representative spectral basis functions estimated from nuisance-corrupted data using
traditional low-rank (left) and our proposed robust low-rank methods (right).
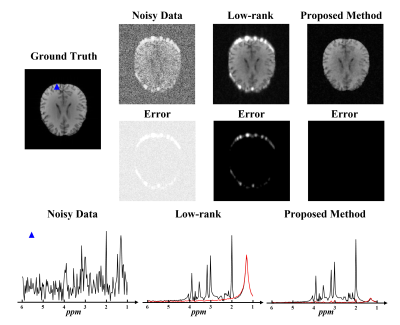
Figure 2: Simulation results. The top two
panels are the spectral integral maps of the ground truth, noisy data, PCA-based low-rank
denoised data and robust low-rank denoised data, with their corresponding error maps. The
bottom panel shows the representative localized spectra from a lipid contaminated spatial
point (blue triangle in the Ground Truth at the top panel). The black line
denotes the noisy data and denoising results and the red line denotes the
error. Our proposed method produced impressive spatiospectral denoising results
without contamination of lipid signals.
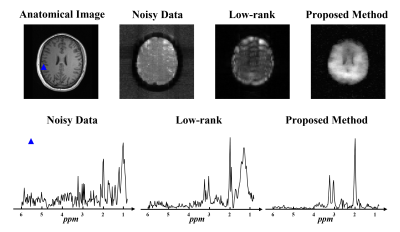
Figure 3: In vivo experimental results. The
top panel shows the anatomical image and spectral integral maps of the original
noisy data, low-rank denoised data, and robust low-rank denoised data. The bottom
panel shows localized spectra from a lipid contaminated spatial point (blue
triangle in the anatomical image in the top panel). Low-rank denoising results
were significantly degraded by residual lipid signals, while our proposed method produced high-quality lipid-free metabolite signals.
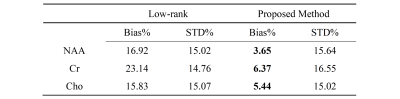
Table 1: Monte-Carlo simulation results. Estimation
bias and standard deviation (STD) of NAA, Cr, and Cho concentrations were
summarized for both low-rank denoising and robust low-rank denoising. Robust
low-rank denoising showed a lower nuisance-introduced bias for all metabolites.
DOI: https://doi.org/10.58530/2022/3533